2021年秋季浙教版数学八年级上学期期中测试模拟卷(适合绍兴、台州、义乌地区)
试卷更新日期:2021-10-25 类型:期中考试
一、单选题
-
1. 下列图形中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列长度的三根小木棒,能搭成三角形的是( )A、1、2、3 B、2、3、4 C、3、3、6 D、2、3、73. 如图,C是直线 外一点,按下列步骤完成作图:( )
2. 下列长度的三根小木棒,能搭成三角形的是( )A、1、2、3 B、2、3、4 C、3、3、6 D、2、3、73. 如图,C是直线 外一点,按下列步骤完成作图:( )⑴以点C为圆心,作能与直线 相交于D、E点的圆弧.
⑵分别以点D和点E为圆心, 长为半径作圆弧,两弧交于点F,连结 、 .
⑶作直线 交 于点G.
根据以上作图过程及所作图形,有如下结论:① ;② ;③ ;④ .其中正确的结论是( )
 A、①②③ B、①③④ C、③④ D、①④4. 如图, 为 的角平分线, ,过 作 于 , 交 的延长线于 ,则下列结论:① ;② ;③ ;④ 其中正确结论的序号有( )
A、①②③ B、①③④ C、③④ D、①④4. 如图, 为 的角平分线, ,过 作 于 , 交 的延长线于 ,则下列结论:① ;② ;③ ;④ 其中正确结论的序号有( ) A、①②③④ B、②③④ C、①②③ D、①②④5. 如图,在 中, 是 边上的高, , , .连接 ,交 的延长线于点E,连接 , .则下列结论:① ;② ;③ ;④ ,其中正确的有( )
A、①②③④ B、②③④ C、①②③ D、①②④5. 如图,在 中, 是 边上的高, , , .连接 ,交 的延长线于点E,连接 , .则下列结论:① ;② ;③ ;④ ,其中正确的有( ) A、①②③ B、①②④ C、①③④ D、①②③④6. 直角三角形斜边上的高与中线分别是5和6,则它的面积是( )A、60 B、50 C、40 D、307. 在 中, , .用无刻度的直尺和圆规在BC边上找一点D , 使 为等腰三角形.下列作法错误的是( )A、
A、①②③ B、①②④ C、①③④ D、①②③④6. 直角三角形斜边上的高与中线分别是5和6,则它的面积是( )A、60 B、50 C、40 D、307. 在 中, , .用无刻度的直尺和圆规在BC边上找一点D , 使 为等腰三角形.下列作法错误的是( )A、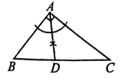 B、
B、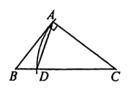 C、
C、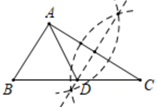 D、
D、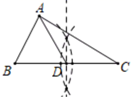 8. 如图,在△ABC中,∠A=90°,∠C=30°,∠ABC的角平分线与线段AC相交于点D,若CD=8,则AD的长( )
8. 如图,在△ABC中,∠A=90°,∠C=30°,∠ABC的角平分线与线段AC相交于点D,若CD=8,则AD的长( ) A、6 B、5 C、4 D、39. 如图,正方形ABCD的边长为8,M在DC上,且DM=2,N是AC上的一动点,则DN+MN的最小值是( )
A、6 B、5 C、4 D、39. 如图,正方形ABCD的边长为8,M在DC上,且DM=2,N是AC上的一动点,则DN+MN的最小值是( )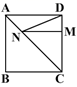 A、8 B、9 C、10 D、1210. 下列命题:①若|a|>|b|,则a>b;②若a+b=0,则|a|≠|b|;③等边三角形的三个内角都相等.④线段垂直平分线上的点到线段两个端点的距离相等.以上命题的逆命题是真命题的有( )A、0 个 B、1 个 C、2 个 D、3 个
A、8 B、9 C、10 D、1210. 下列命题:①若|a|>|b|,则a>b;②若a+b=0,则|a|≠|b|;③等边三角形的三个内角都相等.④线段垂直平分线上的点到线段两个端点的距离相等.以上命题的逆命题是真命题的有( )A、0 个 B、1 个 C、2 个 D、3 个二、填空题
-
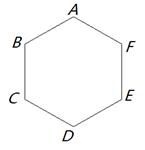
11. 已知点A的坐标为(-2,1+a2),则点A一定在第象限.12. 如图,六根木条钉成一个六边形框架ABCDEF,根据三角形的稳定性要使框架稳固且不活动,至少还需要添根木条.
 13. 面积为48的等腰三角形底边上的高为6,则腰长为 .14. 如图, 平分 , 在 上, 于 , 于 .若 ,则 .
13. 面积为48的等腰三角形底边上的高为6,则腰长为 .14. 如图, 平分 , 在 上, 于 , 于 .若 ,则 .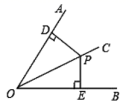 15. 已知一个多边形的每一个外角都相等,一个内角与一个外角的度数之比为7:2,则这个多边形的边数为16. 如图,已知 ,点 在边 上, ,点 在边 上, ,若 则 的长是 .
15. 已知一个多边形的每一个外角都相等,一个内角与一个外角的度数之比为7:2,则这个多边形的边数为16. 如图,已知 ,点 在边 上, ,点 在边 上, ,若 则 的长是 .
三、解答题
-
17. 在一次数学课上,王老师在黑板上画出图(如图所示),并写出四个等式:
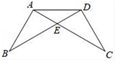
(1)AB=DC,(2)BE=CE , (3)∠B=∠C , (4)∠BAE=∠CDE要求同学从这四个等式中选出两个作为条件,推出△AED是等腰三角形,请你试着完成王老师提出的要求,并说明理由.已知:
求证:△AED是等腰三角形.
18. 如图所示是一个平面直角坐标系,按要求完成下列各小题。 (1)、写出图中的多边形ABCDEF顶点在坐标轴上的点的坐标。(2)、说明点B与点C的纵坐标有什么特点?线段BC与x轴有怎样的位置关系?(3)、写出点E关于y轴的对称点E'的坐标,并指出点E'与点C的位置关系。19. 如图, 中, 的垂直平分线 分别交 , 于点D,E,且 .
(1)、写出图中的多边形ABCDEF顶点在坐标轴上的点的坐标。(2)、说明点B与点C的纵坐标有什么特点?线段BC与x轴有怎样的位置关系?(3)、写出点E关于y轴的对称点E'的坐标,并指出点E'与点C的位置关系。19. 如图, 中, 的垂直平分线 分别交 , 于点D,E,且 .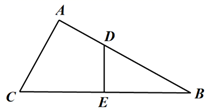
 (1)、求证: ;(2)、若 , ,求 的长.20. 清朝康熙皇帝是我国历史上对数学很有兴趣的帝王近日,西安发现了他的数学专著,其中有一文《积求勾股法》,它对“三边长为3、4、5的整数倍的直角三角形,已知面积求边长”这一问题提出了解法:“若所设者为积数(面积),以积率六除之,平方开之得数,再以勾股弦各率乘之,即得勾股弦之数”.用现在的数学语言表述是:“若直角三角形的三边长分别为3、4、5的整数倍,设其面积为S , 则第一步: =m;第二步: =k;第三步:分别用3、4、5乘以k , 得三边长”.(1)、当面积S等于150时,请用康熙的“积求勾股法”求出这个直角三角形的三边长;(2)、你能证明“积求勾股法”的符合题意性吗?请写出证明过程.21. 如图,在 中,边 的垂直平分线 与边 的垂直平分线 交于点 这两条垂直平分线分别交 于点 .
(1)、求证: ;(2)、若 , ,求 的长.20. 清朝康熙皇帝是我国历史上对数学很有兴趣的帝王近日,西安发现了他的数学专著,其中有一文《积求勾股法》,它对“三边长为3、4、5的整数倍的直角三角形,已知面积求边长”这一问题提出了解法:“若所设者为积数(面积),以积率六除之,平方开之得数,再以勾股弦各率乘之,即得勾股弦之数”.用现在的数学语言表述是:“若直角三角形的三边长分别为3、4、5的整数倍,设其面积为S , 则第一步: =m;第二步: =k;第三步:分别用3、4、5乘以k , 得三边长”.(1)、当面积S等于150时,请用康熙的“积求勾股法”求出这个直角三角形的三边长;(2)、你能证明“积求勾股法”的符合题意性吗?请写出证明过程.21. 如图,在 中,边 的垂直平分线 与边 的垂直平分线 交于点 这两条垂直平分线分别交 于点 . (1)、若 ,求 的度数;(2)、已知 的周长 ,分别连接 ,若 的周长为 ,求 的长.22. 在△ABC中,AB=AC,点D是BC的中点,点E是AD上任意一点
(1)、若 ,求 的度数;(2)、已知 的周长 ,分别连接 ,若 的周长为 ,求 的长.22. 在△ABC中,AB=AC,点D是BC的中点,点E是AD上任意一点 (1)、如图①,连接BE、CE,BE=CE成立吗?说明理由;(2)、若∠BAC=45°,BE的延长线与AC交于点F,且BF⊥AC,如图②,BD= AE成立吗?说明理由.23. 如图,△ABC中,∠C=90°,AB=5cm,BC=3cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒.
(1)、如图①,连接BE、CE,BE=CE成立吗?说明理由;(2)、若∠BAC=45°,BE的延长线与AC交于点F,且BF⊥AC,如图②,BD= AE成立吗?说明理由.23. 如图,△ABC中,∠C=90°,AB=5cm,BC=3cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒. (1)、出发2秒后,求△ABP的周长.(2)、问t为何值时,△BCP为等腰三角形?(3)、另有一点Q,从点C开始,按C→B→A→C的路径运动,且速度为每秒2cm,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动.当t为何值时,直线PQ把△ABC的周长分成相等的两部分?24. 如图
(1)、出发2秒后,求△ABP的周长.(2)、问t为何值时,△BCP为等腰三角形?(3)、另有一点Q,从点C开始,按C→B→A→C的路径运动,且速度为每秒2cm,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动.当t为何值时,直线PQ把△ABC的周长分成相等的两部分?24. 如图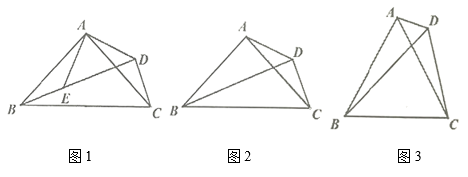 (1)、如图1,等腰 和等腰 中, , , , 三点在同一直线上,求证: ;(2)、如图2,等腰 中, , , 是三角形外一点,且 ,求证: ;(3)、如图3,等边 中, 是形外一点,且 ,
(1)、如图1,等腰 和等腰 中, , , , 三点在同一直线上,求证: ;(2)、如图2,等腰 中, , , 是三角形外一点,且 ,求证: ;(3)、如图3,等边 中, 是形外一点,且 ,① 的度数为;
② , , 之间的关系是.