2021年秋季浙教版数学八年级上学期期中测试模拟卷(适合宁波)
试卷更新日期:2021-10-25 类型:期中考试
一、单选题
-
1. 下列图形中,是轴对称图形的是( )A、
 B、
B、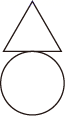 C、
C、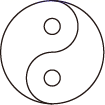 D、
D、 2. 若长度分别是a、3、5的三条线段能组成一个三角形,则a的值可以是( )A、1 B、2 C、4 D、83. 如图所示,点 的表示的数为 , ,以 为圆心, 为半径画弧,交数轴于点 ,则点 表示的数是( )
2. 若长度分别是a、3、5的三条线段能组成一个三角形,则a的值可以是( )A、1 B、2 C、4 D、83. 如图所示,点 的表示的数为 , ,以 为圆心, 为半径画弧,交数轴于点 ,则点 表示的数是( )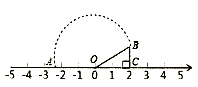 A、 B、 C、 D、4. 对假命题“任何一个角的补角都不小于这个角”举反例,正确的反例是( )A、∠α=60°,∠α的补角∠β=120°,∠β>∠α B、∠α=90°,∠α的补角∠β=90°,∠β=∠α C、∠α=100°,∠α的补角∠β=80°,∠β<∠α D、两个角互为邻补角5. 若 ,则下列不等式一定成立的是( )A、 B、 C、 D、6. 已知△ABC中,a、b、c分别是∠A、∠B、∠C的对边,下列条件中不能判断△ABC是直角三角形的是( )A、∠A:∠B:∠C=3:4:5 B、∠C=∠A﹣∠B C、a2+b2=c2 D、a:b:c=6:8:107. 如图,BC∥EF , BC=EF , 要使得△ABC≌△DEF , 需要补充的条件不能是( )
A、 B、 C、 D、4. 对假命题“任何一个角的补角都不小于这个角”举反例,正确的反例是( )A、∠α=60°,∠α的补角∠β=120°,∠β>∠α B、∠α=90°,∠α的补角∠β=90°,∠β=∠α C、∠α=100°,∠α的补角∠β=80°,∠β<∠α D、两个角互为邻补角5. 若 ,则下列不等式一定成立的是( )A、 B、 C、 D、6. 已知△ABC中,a、b、c分别是∠A、∠B、∠C的对边,下列条件中不能判断△ABC是直角三角形的是( )A、∠A:∠B:∠C=3:4:5 B、∠C=∠A﹣∠B C、a2+b2=c2 D、a:b:c=6:8:107. 如图,BC∥EF , BC=EF , 要使得△ABC≌△DEF , 需要补充的条件不能是( ) A、∠B=∠E B、AB=DE C、AD=CF D、AB∥DE8. 如图,在 中, , 是 边上的高, ,则下列结论中正确的是( )
A、∠B=∠E B、AB=DE C、AD=CF D、AB∥DE8. 如图,在 中, , 是 边上的高, ,则下列结论中正确的是( ) A、 B、 C、 D、9. 如图,由4个相同的直角三角形与中间的小正方形拼成一个大正方形,若大正方形面积是9,小正方形面积是1,直角三角形较长直角边为a,较短直角边为b,则ab的值是( )
A、 B、 C、 D、9. 如图,由4个相同的直角三角形与中间的小正方形拼成一个大正方形,若大正方形面积是9,小正方形面积是1,直角三角形较长直角边为a,较短直角边为b,则ab的值是( )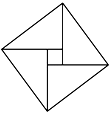 A、4 B、6 C、8 D、1010. 如图:在△ABC中,∠B=45°,D是AB边上一点,连接CD,过A作AF⊥CD交CD于G,交BC于点F.已知AC=CD,CG=3,DG=1,则下列结论正确的是( )
A、4 B、6 C、8 D、1010. 如图:在△ABC中,∠B=45°,D是AB边上一点,连接CD,过A作AF⊥CD交CD于G,交BC于点F.已知AC=CD,CG=3,DG=1,则下列结论正确的是( )
①∠ACD=2∠FAB ② ③ ④ AC=AF
A、①②③ B、①②③④ C、②③④ D、①③④二、填空题
-
11. 不等式2x﹣1≤3x+2的负整数解的和是 .12. 在 中,两直角边的长分别为7和24, 则其斜边上的中线长为.13. 不等式组 的解集是.14. 如图,点P是∠AOB内任意一点,OP=9,M、N分别是射线OA和OB上的动点,若△PMN周长的最小值为9,则∠AOB=°.
 15. 为等边三角形,点D为 边上一点,以 为边做等边三角形 ,使点E,A在直线 的同侧,连接 ,则 的度数为 .
15. 为等边三角形,点D为 边上一点,以 为边做等边三角形 ,使点E,A在直线 的同侧,连接 ,则 的度数为 .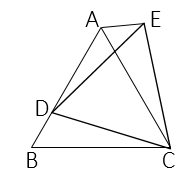 16. 如图所示,∠E=∠F=90°,∠B=∠C , AE=AF . 给出下列结论:①∠1=∠2;②BE=CF;③△ACN≌△ABM;④CD=DN . 其中正确的结论是 . (将你认为正确的结论的序号都填上)
16. 如图所示,∠E=∠F=90°,∠B=∠C , AE=AF . 给出下列结论:①∠1=∠2;②BE=CF;③△ACN≌△ABM;④CD=DN . 其中正确的结论是 . (将你认为正确的结论的序号都填上)
三、解答题
-
17. 解不等式(组):(1)、解不等式(2)、解不等式组:18. (阅读)例题:在等腰三角形 中,若 ,求 的度数.
点点同学在思考时是这样分析的: , 都可能是顶角或底角,因此需要进行分类.他认为画“树状图”可以帮我们不重复,不遗漏地分类(如图),据此可求出 的度数.
 (1)、(解答)
(1)、(解答)由以上思路,可得 的度数为;
(2)、(应用)将一个边长为5,12,13的直角三角形拼上一个三角形后可以拼成一个等腰三角形,图2就是其中的一种拼法.请你利用备用图画出三种可能的情形,使得拼成的等腰三角形腰长为13.
(注意:请对所拼成图形中的线段长度标注数据)
 19. 如图,在△ABC中,AB=AC , ∠BAC=90°,分别过点B , C向过点A的直线作垂线,垂足分别为点E , F .
19. 如图,在△ABC中,AB=AC , ∠BAC=90°,分别过点B , C向过点A的直线作垂线,垂足分别为点E , F .
求证:
(1)、△ABE≌△CAF;(2)、EF=BE+CF .20. 如图1,A(﹣2,0),B(0,4),以B点为直角顶点在第二象限作等腰直角△ABC.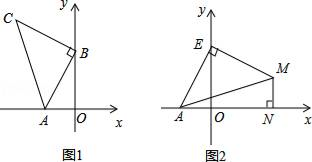 (1)、求C点的坐标;(2)、在坐标平面内是否存在一点P,使△PAB与△ABC全等?若存在,求出P点坐标,若不存在,请说明理由;(3)、如图2,点E为y轴正半轴上一动点,以E为直角顶点作等腰直角△AEM,过M作MN⊥x轴于N,求OE﹣MN的值.21. 现计划把甲种货物306吨和乙种货物230吨运往某地.已知有A、B两种不同规格的货车共50辆,如果每辆A型货车最多可装甲种货物7吨和乙种货物3吨,每辆B型货车最多可装甲种货物5吨和乙种货物7吨.(1)、装货时按此要求安排A、B两种货车的辆数,共有几种方案?(2)、使用A型车每辆费用为600元,使用B型车每辆费用800元.在上述方案中,哪个方案运费最省?最省的运费是多少元?(3)、在(2)的方案下,现决定对货车司机发共2100元的安全奖,已知每辆A型车奖金为m元.每辆B型车奖金为n元,38<m<n.且m、n均为整数,求此次奖金发放的具体方案.22. 在四边形 中,已知 , , , .
(1)、求C点的坐标;(2)、在坐标平面内是否存在一点P,使△PAB与△ABC全等?若存在,求出P点坐标,若不存在,请说明理由;(3)、如图2,点E为y轴正半轴上一动点,以E为直角顶点作等腰直角△AEM,过M作MN⊥x轴于N,求OE﹣MN的值.21. 现计划把甲种货物306吨和乙种货物230吨运往某地.已知有A、B两种不同规格的货车共50辆,如果每辆A型货车最多可装甲种货物7吨和乙种货物3吨,每辆B型货车最多可装甲种货物5吨和乙种货物7吨.(1)、装货时按此要求安排A、B两种货车的辆数,共有几种方案?(2)、使用A型车每辆费用为600元,使用B型车每辆费用800元.在上述方案中,哪个方案运费最省?最省的运费是多少元?(3)、在(2)的方案下,现决定对货车司机发共2100元的安全奖,已知每辆A型车奖金为m元.每辆B型车奖金为n元,38<m<n.且m、n均为整数,求此次奖金发放的具体方案.22. 在四边形 中,已知 , , , .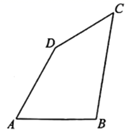 (1)、连接 ,试判断 的形状,并说明理由;(2)、求 的度数23. 图①是美丽的弦图,包含四个全等的直角三角形.
(1)、连接 ,试判断 的形状,并说明理由;(2)、求 的度数23. 图①是美丽的弦图,包含四个全等的直角三角形. (1)、弦图中包含了一大一小两个正方形,已知每个直角三角形较长的直角边长为a,较短的直角边长为b,斜边长为c,结合图①,试验证勾股定理;(2)、如图②,将这四个直角三角形紧密拼接,形成飞镖状,已知外围轮廓(实线)的周长为24,OC=3,求该飞镖状图案的面积;(3)、如图③,将八个全等的直角三角形紧密拼接,记正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1 , S2 , S3 , 若S1+S2+S3=16,则S2= .24. 已知 是等边三角形,点D是AC的中点,点E在射线BC上,点F在射线BA上, .
(1)、弦图中包含了一大一小两个正方形,已知每个直角三角形较长的直角边长为a,较短的直角边长为b,斜边长为c,结合图①,试验证勾股定理;(2)、如图②,将这四个直角三角形紧密拼接,形成飞镖状,已知外围轮廓(实线)的周长为24,OC=3,求该飞镖状图案的面积;(3)、如图③,将八个全等的直角三角形紧密拼接,记正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1 , S2 , S3 , 若S1+S2+S3=16,则S2= .24. 已知 是等边三角形,点D是AC的中点,点E在射线BC上,点F在射线BA上, .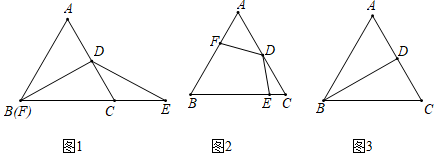 (1)、如图1,若点F与B点重合,求证: ;(2)、如图2,若点E在线段BC上,点F在线段BA上,求 的值;(3)、如图3,若 ,直接写出 的度数为 .
(1)、如图1,若点F与B点重合,求证: ;(2)、如图2,若点E在线段BC上,点F在线段BA上,求 的值;(3)、如图3,若 ,直接写出 的度数为 .