2021年秋季浙教版数学八年级上学期期中测试模拟卷(适合嘉兴、舟山、金华、丽水、湖州、衢州)
试卷更新日期:2021-10-25 类型:期中考试
一、单选题
-
1. 下列图形中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 有两根6cm , 8cm的木棒,以这两根木棒做一个三角形,可以选用第三根木棒的长为( )A、2cm B、6cm C、14cm D、16cm3. 如图,一扇窗户打开后,用窗钩AB可将其固定,这里所运用的几何原理是( )
2. 有两根6cm , 8cm的木棒,以这两根木棒做一个三角形,可以选用第三根木棒的长为( )A、2cm B、6cm C、14cm D、16cm3. 如图,一扇窗户打开后,用窗钩AB可将其固定,这里所运用的几何原理是( )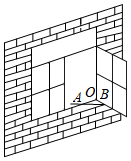 A、两点确定一条直线 B、两点之间线段最短 C、三角形的稳定性 D、垂线段最短4. 下列选项中的图形与给出的图形全等的是( )
A、两点确定一条直线 B、两点之间线段最短 C、三角形的稳定性 D、垂线段最短4. 下列选项中的图形与给出的图形全等的是( )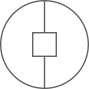 A、
A、 B、
B、 C、
C、 D、
D、 5. 若 ,则下列式子成立的是( )A、 B、 C、 D、6. 如图, 是等腰三角形 底边 上的中线, 平分 ,交 于点 , , ,则 的面积是( )
5. 若 ,则下列式子成立的是( )A、 B、 C、 D、6. 如图, 是等腰三角形 底边 上的中线, 平分 ,交 于点 , , ,则 的面积是( ) A、4 B、6 C、8 D、127. 甲、乙两位同学分别用尺规作图法作∠AOB的平分线OC,则他们两人的作图方法( )
A、4 B、6 C、8 D、127. 甲、乙两位同学分别用尺规作图法作∠AOB的平分线OC,则他们两人的作图方法( ) A、甲、乙两人均正确 B、甲正确,乙不正确 C、甲不正确,乙正确 D、甲、乙两人均不正确8. 如图,等腰Rt△ABC中,∠BAC=90°,AD⊥BC于D , ∠ABC的平分线分别交AC、AD于E、F两点,M为EF的中点,延长AM交BC于点N , 连接DM , 下列结论:①AE=AF;②DF=DN;③AE=CN;④△AMD和△DMN的面积相等,其中错误的结论个数是( )
A、甲、乙两人均正确 B、甲正确,乙不正确 C、甲不正确,乙正确 D、甲、乙两人均不正确8. 如图,等腰Rt△ABC中,∠BAC=90°,AD⊥BC于D , ∠ABC的平分线分别交AC、AD于E、F两点,M为EF的中点,延长AM交BC于点N , 连接DM , 下列结论:①AE=AF;②DF=DN;③AE=CN;④△AMD和△DMN的面积相等,其中错误的结论个数是( )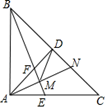 A、3个 B、2个 C、1个 D、0个9. 如图,圆柱形容器中,高为1.2 m,底面周长为1m,在容器内壁离容器底部0.3 m的点B处有一蚊子,此时一只壁虎正好在容器外壁,离容器上沿0.3 m与蚊子相对的点A处,则壁虎捕捉蚊子的最短距离为( )m(容器厚度忽略不计).
A、3个 B、2个 C、1个 D、0个9. 如图,圆柱形容器中,高为1.2 m,底面周长为1m,在容器内壁离容器底部0.3 m的点B处有一蚊子,此时一只壁虎正好在容器外壁,离容器上沿0.3 m与蚊子相对的点A处,则壁虎捕捉蚊子的最短距离为( )m(容器厚度忽略不计). A、1.8 B、1.5 C、1.2 D、1.310. 国庆假期中,小华与同学去玩探宝游戏,按照探宝图,他们从门口 处出发先往东走 ,又往北走 ,遇到障碍后又往西走 ,再向北走到 处往东拐,仅走了 ,就找到了宝藏,则门口 到藏宝点 的直线距离是( )
A、1.8 B、1.5 C、1.2 D、1.310. 国庆假期中,小华与同学去玩探宝游戏,按照探宝图,他们从门口 处出发先往东走 ,又往北走 ,遇到障碍后又往西走 ,再向北走到 处往东拐,仅走了 ,就找到了宝藏,则门口 到藏宝点 的直线距离是( ) A、20km B、14km C、11km D、10km
A、20km B、14km C、11km D、10km二、填空题
-
11. “x与5的差小于4”用不等式可表示为 .12. 命题“若a2>b2 , 则a>b”的逆命题是 , 该逆命题是(填“真”或“假”)命题.13. 如图,在 中, 是 的角平分线, ,垂足为E,若 .
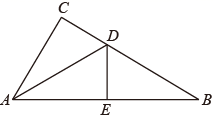 14. 如图,在△ABC中,∠C =45°,AB的垂直平分线交AB于点E , 交BC于点D;AC的垂直平分线交AC于点G , 交BC于点F , 连接 AD , AF . 若AF=2cm,BC=8cm,则DF=cm.
14. 如图,在△ABC中,∠C =45°,AB的垂直平分线交AB于点E , 交BC于点D;AC的垂直平分线交AC于点G , 交BC于点F , 连接 AD , AF . 若AF=2cm,BC=8cm,则DF=cm. 15. 如图,△ABC中,点P、点Q是边BC上的两个点,若BP=PQ=QC=AP=AQ , 则∠PAC的度数为°.
15. 如图,△ABC中,点P、点Q是边BC上的两个点,若BP=PQ=QC=AP=AQ , 则∠PAC的度数为°. 16. 如图,在 中, ,以点 为圆心,适当长为半径作弧,交 于 两点,再分别以 两点为圆心,大于 的长为半径作弧,两弧相交于点 ,作射线 交 于点 ,则点 与线段 上的点的连线中,长度最短的线段的长为.
16. 如图,在 中, ,以点 为圆心,适当长为半径作弧,交 于 两点,再分别以 两点为圆心,大于 的长为半径作弧,两弧相交于点 ,作射线 交 于点 ,则点 与线段 上的点的连线中,长度最短的线段的长为.
三、解答题
-
17. 作图题(保留作图痕迹)已知: 和两点M、N,求作:一点P,使点P到 两边的距离相等,且 .
 18. 如图,点A , D , B , E在一条直线上 , , .
18. 如图,点A , D , B , E在一条直线上 , , .求证: .
 19. 如图,在一条东西走向的河流的一侧有一村庄C,河边原有两个取水点A,B,其中AB=AC,由于某种原因,由C到A的路现在已经不通,该村为方便村民取水决定在河边新建一个取水点H(A、H、B在同一条直线上),并新修一条路CH,测得CB=1.5千米,CH=1.2千米,HB=0.9千米.
19. 如图,在一条东西走向的河流的一侧有一村庄C,河边原有两个取水点A,B,其中AB=AC,由于某种原因,由C到A的路现在已经不通,该村为方便村民取水决定在河边新建一个取水点H(A、H、B在同一条直线上),并新修一条路CH,测得CB=1.5千米,CH=1.2千米,HB=0.9千米. (1)、试判断△CHB是不是直角三角形,并说明理由;(2)、求新路CH比原路CA短多少千米.20. 在 中, , ,直线 经过点C,且 于D, 于E,
(1)、试判断△CHB是不是直角三角形,并说明理由;(2)、求新路CH比原路CA短多少千米.20. 在 中, , ,直线 经过点C,且 于D, 于E, (1)、当直线 绕点C旋转到图1的位置时,求证:
(1)、当直线 绕点C旋转到图1的位置时,求证:① ;
② ;
(2)、当直线 绕点C旋转到图2的位置时,猜想 、 、 之间的关系,并请给出证明.21. 已知,如图△ABC为等边三角形,AE=CD,AD、BE相交于点P. (1)、求证: ;(2)、求∠BPQ的度数;(3)、若 于Q,PQ=6,PE=2,求BE的长.22. 数学课上,探讨角平分线的作法时,李老师用直尺和圆规作角平分线,方法如下:
(1)、求证: ;(2)、求∠BPQ的度数;(3)、若 于Q,PQ=6,PE=2,求BE的长.22. 数学课上,探讨角平分线的作法时,李老师用直尺和圆规作角平分线,方法如下:根据以下情境,解决下列问题:
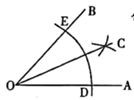
作法:①在 和 上分别截取 、 ,使 .
②分别以D、E为圆心,以大于 的长为半径作弧,两弧在 内交于点C.
③作射线 .则 就是 的平分线.
(1)、李老师用尺规作角平分线时,用到的三角形全等的判定方法是.小聪只带了直角三角板,他发现利用三角板也可以作角平分线,方法如下:

步骤:①利用三角板上的刻度,在 和 上分别截取 、 ,使 .
②分别过M、N作 、 的垂线,交于点P.
③作射线 .则 为 的平分线.
(2)、小聪的作法正确吗?请说明理由.23. 如图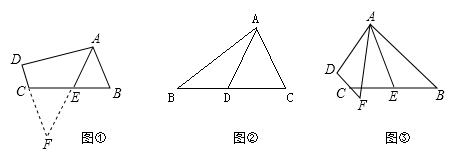 (1)、如图①,在四边形ABCD中,AB∥CD,点E是BC的中点,若AE是∠BAD的平分线,试判断AB,AD,DC之间的等量关系。
(1)、如图①,在四边形ABCD中,AB∥CD,点E是BC的中点,若AE是∠BAD的平分线,试判断AB,AD,DC之间的等量关系。解决此问题可以用如下方法:延长AE交DC的延长线于点F,易证△AEB≌△FEC得到AB=FC,从而把AB,AD,DC转化在一个三角形中即可判断。
AB,AD,DC之间的等量关系;
(2)、同题探究;①如图②,AD是△ABC的中线,AB=6,AC=4,求AD的范围:
②如图③,在四边形ABCD中,AB∥CD,AF与DC的延长线交于点F,点E是BC的中点,若AE是∠BAF的平分线,试探究AB,AF,CF之间的等量关系,并证明你的结论。
24. 阅读与理解:折纸,常常能为证明一个命题提供思路和方法.例如,在△ABC中,AB>AC(如图),怎样证明∠C>∠B呢?

分析:把AC沿∠A的角平分线AD翻折,因为AB>AC,所以点C落在AB上的点C'处,即AC=AC',据以上操作,易证明△ACD≌△AC'D,所以∠AC'D=∠C,又因为∠AC'D>∠B,所以∠C>∠B.
感悟与应用:
 (1)、如图(a),在△ABC中,∠ACB=90°,∠B=30°,CD平分∠ACB,试判断AC和AD、BC之间的数量关系,并说明理由;(2)、如图(b),在四边形ABCD中,AC平分∠BAD,AC=16,AD=8,DC=BC=12,
(1)、如图(a),在△ABC中,∠ACB=90°,∠B=30°,CD平分∠ACB,试判断AC和AD、BC之间的数量关系,并说明理由;(2)、如图(b),在四边形ABCD中,AC平分∠BAD,AC=16,AD=8,DC=BC=12,①求证:∠B+∠D=180°;
②求AB的长.