2021年秋季浙教版数学八年级上学期期中测试模拟卷(适合杭州地区)
试卷更新日期:2021-10-25 类型:期中考试
一、单选题
-
1. 下列对称轴条数最多的图形是( )A、角 B、等边三角形 C、正方形 D、圆2. 下列各式中,是一元一次不等式的是( )A、 B、 C、 D、3. 下列长度的三条线段,能构成三角形的是( )A、1,2,3 B、3,4,5 C、5,12,17 D、6,8,204. 如图,在 ACE中,点D在AC边上,点B在CE延长线上,连接BD , 若∠A=47°,∠B=55°,∠C=43°,则∠DFE的度数是( )
 A、125° B、45° C、135° D、145°5. 已知 ,则下列四个不等式中,不正确的是( )A、 B、 C、 D、6. 若直角三角形的两条直角边长分别为 、 ,则该直角三角形斜边上的中线为( )A、 B、 C、 D、7. 等腰三角形 中, ,一边上的中线 将这个三角形的周长分为 和 两部分,则这个等腰三角形的底边长为( )A、7 B、7或11 C、11 D、7或108. 如图是由四个全等的直角三角形与一个小正方形拼成的大正方形.若小正方形边长为 ,大正方形边长为 ,则一个直角三角形的面积等于( )
A、125° B、45° C、135° D、145°5. 已知 ,则下列四个不等式中,不正确的是( )A、 B、 C、 D、6. 若直角三角形的两条直角边长分别为 、 ,则该直角三角形斜边上的中线为( )A、 B、 C、 D、7. 等腰三角形 中, ,一边上的中线 将这个三角形的周长分为 和 两部分,则这个等腰三角形的底边长为( )A、7 B、7或11 C、11 D、7或108. 如图是由四个全等的直角三角形与一个小正方形拼成的大正方形.若小正方形边长为 ,大正方形边长为 ,则一个直角三角形的面积等于( ) A、 B、 C、 D、9. 下列命题:①形状相同的两个三角形是全等形;②在两个三角形中,相等的角是对应角,相等的边是对应边;③全等三角形对应边上的高、中线及对应角平分线分别相等;④到已知角两边距离相等的点都在同一条直线上.其中真命题有( )A、1个 B、2个 C、3个 D、4个10. 如图,已知 的大小为 , 是 内部的一个定点,且 ,点 , 分别是 、 上的动点,若 周长的最小值等于 ,则 的大小为( )
A、 B、 C、 D、9. 下列命题:①形状相同的两个三角形是全等形;②在两个三角形中,相等的角是对应角,相等的边是对应边;③全等三角形对应边上的高、中线及对应角平分线分别相等;④到已知角两边距离相等的点都在同一条直线上.其中真命题有( )A、1个 B、2个 C、3个 D、4个10. 如图,已知 的大小为 , 是 内部的一个定点,且 ,点 , 分别是 、 上的动点,若 周长的最小值等于 ,则 的大小为( )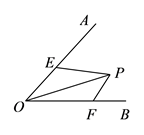 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 用不等式表示: 的2倍与5的和是非负数.12. 如图,在△ABC中,AB的中垂线交BC于D,AC的中垂线交BC于E,若∠BAC=126°,则∠EAD=°
 13. 命题“等腰三角形两底角相等”的逆命题是。14. 已知 中, , ,如果 是边 的中点,那么 度.15. 如图,已知∠AOB= 30°,点P在边OA上,OD=DP= 14,点E,F在边OB上,PE=PF.若EF=6,则OF的长为
13. 命题“等腰三角形两底角相等”的逆命题是。14. 已知 中, , ,如果 是边 的中点,那么 度.15. 如图,已知∠AOB= 30°,点P在边OA上,OD=DP= 14,点E,F在边OB上,PE=PF.若EF=6,则OF的长为 16. 已知 是等边三角形,点D、E分别在AC、BC上,且 ,则 .
16. 已知 是等边三角形,点D、E分别在AC、BC上,且 ,则 .
三、计算题
-
17. 解下列不等式(组):(1)、 ;(2)、 .18. 如图,AD平分∠BAC,DE⊥AB,DF⊥AC,垂足分别为点E,F,DB=DC.
 (1)、求证:BE=CF;(2)、如果BD//AC,∠DAF=15°,求证:AB=2DF.19. 如图,在△ABC中,AB=AC,D是BC边上的中点,连结AD,BE平分∠ABC交AC于点E,过点E作EF∥BC交AB于点F.
(1)、求证:BE=CF;(2)、如果BD//AC,∠DAF=15°,求证:AB=2DF.19. 如图,在△ABC中,AB=AC,D是BC边上的中点,连结AD,BE平分∠ABC交AC于点E,过点E作EF∥BC交AB于点F. (1)、若∠C=38°,求∠BAD的度数;(2)、求证:FB=FE.20. 如图,C为线段 上一动点(不与点A,E重合),在 同侧分别作正三角形 和正三角形 (正三角形也叫等边三角形,它的三条边都相等,三个内角都等于60°), 与 交于点O, 与 交于点P, 与 交于点Q,连接 .
(1)、若∠C=38°,求∠BAD的度数;(2)、求证:FB=FE.20. 如图,C为线段 上一动点(不与点A,E重合),在 同侧分别作正三角形 和正三角形 (正三角形也叫等边三角形,它的三条边都相等,三个内角都等于60°), 与 交于点O, 与 交于点P, 与 交于点Q,连接 .试说明:
 (1)、 ;(2)、填空 °;(3)、 .21. 如图所示,在△ABC中,AB=8,AC=6,DE是BC的垂直平分线,交BC于点D,交AB于点E,AF⊥BC于点F。
(1)、 ;(2)、填空 °;(3)、 .21. 如图所示,在△ABC中,AB=8,AC=6,DE是BC的垂直平分线,交BC于点D,交AB于点E,AF⊥BC于点F。 (1)、若∠BAC=90°,求BE的长。(2)、若DF= ,试说明:△ABC为直角三角形。
(1)、若∠BAC=90°,求BE的长。(2)、若DF= ,试说明:△ABC为直角三角形。