湘教版九年级上册初中数学期中复习专题2 反比例函数的图象与性质
试卷更新日期:2021-10-24 类型:复习试卷
一、单选题
-
1. 根据反比例函数的性质、联系化学学科中的溶质质量分数的求法以及生活体验等,判定下列有关函数 (a为常数且 )的性质表述中,正确的是( )
①y随x的增大而增大;②y随x的增大而减小;③ ;④
A、①③ B、①④ C、②③ D、②④2. 已知点 , 都在反比例函数 的图象上,且 ,则 , 的关系是( )A、 B、 C、 D、3. 已知双曲线 过点(3, )、(1, )、(-2, ),则下列结论正确的是( )A、 B、 C、 D、4. 如图,点A在曲线到 上,点B在双曲线 上, 轴,点C是x轴上一点,连接 、 ,若 的面积是6,则k的值( )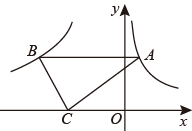 A、-6 B、-8 C、-10 D、-125. 在反比例函数 ( 为常数)上有三点 , , ,若 ,则 , , 的大小关系为( )A、 B、 C、 D、6. 若点 , , 都在反比例函数 的图象上,则 , , 的大小关系是( )A、 B、 C、 D、7. 已知点 在反比例函数 的图象上.若 ,则( )A、 B、 C、 D、8. 下列说法正确的是( )
A、-6 B、-8 C、-10 D、-125. 在反比例函数 ( 为常数)上有三点 , , ,若 ,则 , , 的大小关系为( )A、 B、 C、 D、6. 若点 , , 都在反比例函数 的图象上,则 , , 的大小关系是( )A、 B、 C、 D、7. 已知点 在反比例函数 的图象上.若 ,则( )A、 B、 C、 D、8. 下列说法正确的是( )①反比例函数 中自变量x的取值范围是 ;②点 在反比例函数 的图象上;③反比例函数 的图象,在每一个象限内,y随x的增大而增大.
A、①② B、①③ C、②③ D、①②③9. 已知三个点(x1 , y1),(x2 , y2),(x3 , y3)在反比例函数y= 的图象上,其中x1<x2<0<x3 , 下列结论中正确的是( )A、y2<y1<0<y3 B、y1<y2<0<y3 C、y3<0<y2<y1 D、y3<0<y1<y210. 已知反比例函数 ,则下列描述错误的是( )A、图象位于第一,第三象限 B、图象必经过点 C、图象不可能与坐标轴相交 D、 随 的增大而减小二、填空题
-
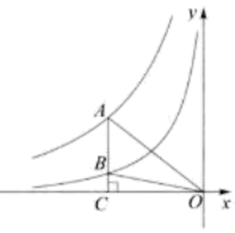
11. 在平面直角坐标系中,一次函数 与反比例函数 的图象交于 , 两点,则 的值是.12. 若点 、 、 都在反比例函数 (k为常数)的图象上,则 、 、 的大小关系为 .13. 如图,点A是反比例函数 图象上一点, 轴于点C且与反比例函数 的图象交于点B , ,连接OA , OB , 若 的面积为6,则 .
 14. 已知点 和点 在反比例函数 的图象上,则 与 的大小关系是 .15. 在平面直角坐标系 中,若反比例函数 的图象经过点 和点 ,则 的值为 .
14. 已知点 和点 在反比例函数 的图象上,则 与 的大小关系是 .15. 在平面直角坐标系 中,若反比例函数 的图象经过点 和点 ,则 的值为 .三、解答题
-
16. 如图,点A在反比例函数 的图象上,过点A作y轴的平行线交反比例函数 的图象于点B , 点C在y轴上,若 的面积为8,求k的值.
 17. 如图,正比例函数 的图象与反比例函数 的图象交于A、B两点,点C在x轴负半轴上,AC=AO,△ACO的面积为12.
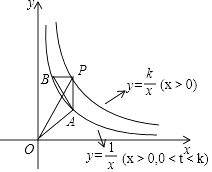
17. 如图,正比例函数 的图象与反比例函数 的图象交于A、B两点,点C在x轴负半轴上,AC=AO,△ACO的面积为12.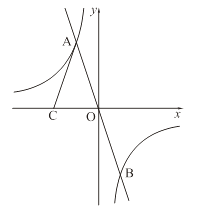 (1)、求k的值;(2)、根据图象,当 时,写出自变量 的取值范围.18. 如图所示,Rt△PAB的直角顶点P(3,4)在函数y= (x>0)的图象上,顶点A、B在函数y= (x>0,0<t<k)的图象上,PA∥y轴,连接OP,OA,记△OPA的面积为S△OPA , △PAB的面积为S△PAB , 设w=S△OPA﹣S△PAB .
(1)、求k的值;(2)、根据图象,当 时,写出自变量 的取值范围.18. 如图所示,Rt△PAB的直角顶点P(3,4)在函数y= (x>0)的图象上,顶点A、B在函数y= (x>0,0<t<k)的图象上,PA∥y轴,连接OP,OA,记△OPA的面积为S△OPA , △PAB的面积为S△PAB , 设w=S△OPA﹣S△PAB .①求k的值以及w关于t的表达式;
②若用wmax和wmin分别表示函数w的最大值和最小值,令T=wmax+a2﹣a,其中a为实数,求Tmin .
 19. 丽水苛公司将“丽水山耕”农副产品运往杭州市场进行销售.记汽车行驶时间为t小时,平均速度为v千米/小时(汽车行驶速度不超过100千米/小时).根据经验,v,t的一组对应值如下表:
19. 丽水苛公司将“丽水山耕”农副产品运往杭州市场进行销售.记汽车行驶时间为t小时,平均速度为v千米/小时(汽车行驶速度不超过100千米/小时).根据经验,v,t的一组对应值如下表:v(千米/小时)
75
80
85
90
95
t(小时)
4.00
3.75
3.53
3.33
3.16
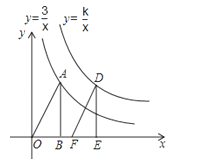
(1)、根据表中的数据,求出平均速度v(千米/小时)关于行驶时间t(小时)的函数表达式;(2)、汽车上午7:30从丽水出发,能否在上午10:00之前到达杭州市?请说明理由:(3)、若汽车到达杭州市场的行驶时间t满足3.5≤t≤4,求平均速度v的取值范围.20. 如图,点A(1,a)在反比例函数y=(x>0)的图象上,AB垂直于x轴,垂足为点B,将△ABO沿x轴向右平移2个单位长度,得到Rt△DEF,点D落在反比例函数y=(x>0)的图象上.(1)求点A的坐标;
(2)求k值.
四、综合题
-
21. 如图,点A在反比例函数 的图象位于第一象限的分支上,过点A作AB⊥y轴于点B,S△AOB=2.
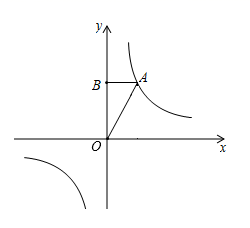 (1)、求该反比例函数的表达式,(2)、若P(x1 , y1)、Q(x2 , y2)是反比例函数 图象上的两点,且x1 x2 , y1 y2 , 指出点P、Q各位于哪个象限,并简要说明理由.22. 如图,在矩形OABC中,OA=3,OC=2,点F在AB上(点F不与点A , B重合),OA , OC分别在x轴,y轴上,过点F的反比例函数 (k>0)的图象与BC边交于点E .
(1)、求该反比例函数的表达式,(2)、若P(x1 , y1)、Q(x2 , y2)是反比例函数 图象上的两点,且x1 x2 , y1 y2 , 指出点P、Q各位于哪个象限,并简要说明理由.22. 如图,在矩形OABC中,OA=3,OC=2,点F在AB上(点F不与点A , B重合),OA , OC分别在x轴,y轴上,过点F的反比例函数 (k>0)的图象与BC边交于点E .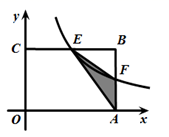 (1)、点E的坐标为 , 点F的坐标为(用含k的式子表示).(2)、求k为何值时,△EFA的面积最大,最大面积是多少?23. 在矩形 中, , .分别以 所在直线为 轴和 轴,建立如图所示的平面直角坐标系. 是边 上一点,过点 的反比例函数 图象与 边交于点 .
(1)、点E的坐标为 , 点F的坐标为(用含k的式子表示).(2)、求k为何值时,△EFA的面积最大,最大面积是多少?23. 在矩形 中, , .分别以 所在直线为 轴和 轴,建立如图所示的平面直角坐标系. 是边 上一点,过点 的反比例函数 图象与 边交于点 .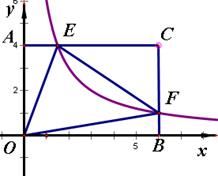 (1)、请用k表示点E,F的坐标;(2)、若 的面积为 ,求反比例函数的解析式.
(1)、请用k表示点E,F的坐标;(2)、若 的面积为 ,求反比例函数的解析式.