北师大版初中数学2021-2022学年八年级上学期期中测试模拟卷(一)
试卷更新日期:2021-10-23 类型:期中考试
一、单选题
-
1. 在实数 ,0, , 中,无理数是( )A、 B、0 C、 D、2. 如图是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案.现有五种正方形纸片,面积分别是1,2,3,4,5,选取其中三块(可重复选取)按图的方式组成图案,使所围成的三角形是面积最大的直角三角形,则选取的三块纸片的面积分别是( )
 A、1,4,5 B、2,3,5 C、3,4,5 D、2,2,43. 在平面直角坐标系中,若点P(a-3,1)与点Q(2,b+1)关于x轴对称,则a+b的值是( )A、1 B、2 C、3 D、44. 下列数中,在 与 之间的是( )A、3 B、4 C、5 D、65. 下列计算中,正确的是( )A、 B、 C、 D、6. 我国古代数学著作《九章算术》记载了一道有趣的问题.原文是:今有池方一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问水深、葭长各几何.译为:有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺,如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面,水的深度与这根芦苇的长度分别是多少?设芦苇的长度是 尺.根据题意,可列方程为( )
A、1,4,5 B、2,3,5 C、3,4,5 D、2,2,43. 在平面直角坐标系中,若点P(a-3,1)与点Q(2,b+1)关于x轴对称,则a+b的值是( )A、1 B、2 C、3 D、44. 下列数中,在 与 之间的是( )A、3 B、4 C、5 D、65. 下列计算中,正确的是( )A、 B、 C、 D、6. 我国古代数学著作《九章算术》记载了一道有趣的问题.原文是:今有池方一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问水深、葭长各几何.译为:有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺,如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面,水的深度与这根芦苇的长度分别是多少?设芦苇的长度是 尺.根据题意,可列方程为( )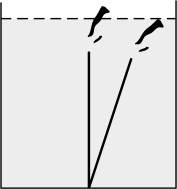 A、 B、 C、 D、7. 一次函数 的图象过点 , , ,则( )A、 B、 C、 D、8. 数经历了从自然数到有理数,到实数,再到复数的发展过程,数学中把形如a+bi(a,b为实数)的数叫做复数,用z=a+bi表示,任何一个复数z=a+bi在平面直角坐标系中都可以用有序数对Z(a,b)表示,如:z=1+2i表示为Z(1,2),则z=2﹣i可表示为( )A、Z(2,0) B、Z(2,﹣1) C、Z(2,1) D、Z(﹣1,2)9. 如图, 中, ,将 沿DE翻折,使点A与点B重合,则CE的长为( )
A、 B、 C、 D、7. 一次函数 的图象过点 , , ,则( )A、 B、 C、 D、8. 数经历了从自然数到有理数,到实数,再到复数的发展过程,数学中把形如a+bi(a,b为实数)的数叫做复数,用z=a+bi表示,任何一个复数z=a+bi在平面直角坐标系中都可以用有序数对Z(a,b)表示,如:z=1+2i表示为Z(1,2),则z=2﹣i可表示为( )A、Z(2,0) B、Z(2,﹣1) C、Z(2,1) D、Z(﹣1,2)9. 如图, 中, ,将 沿DE翻折,使点A与点B重合,则CE的长为( )
 A、 B、2 C、 D、10. 如图,在平面直角坐标系中,将△ABO沿x轴向右滚动到△AB1C1的位置,再到△A1B1C2的位置……依次进行下去,若已知点A(4,0),B(0,3),则点C100的坐标为( )
A、 B、2 C、 D、10. 如图,在平面直角坐标系中,将△ABO沿x轴向右滚动到△AB1C1的位置,再到△A1B1C2的位置……依次进行下去,若已知点A(4,0),B(0,3),则点C100的坐标为( )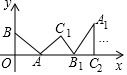 A、 B、 C、 D、11. 如图,直线 经过点 ,则不等式 的解集为( )
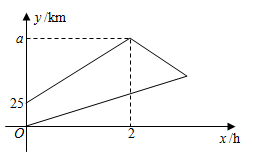
A、 B、 C、 D、11. 如图,直线 经过点 ,则不等式 的解集为( )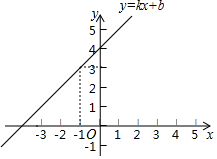 A、 B、 C、 D、12. 一辆快车和一辆慢车将一批物资从甲地运往乙地,其中快车送达后立即沿原路返同,且往返速度的大小不变,两车离甲地的距离 (单位: )与慢车行驶时间 (单位: )的函数关系如图,则两车先后两次相遇的间隔时间是( )
A、 B、 C、 D、12. 一辆快车和一辆慢车将一批物资从甲地运往乙地,其中快车送达后立即沿原路返同,且往返速度的大小不变,两车离甲地的距离 (单位: )与慢车行驶时间 (单位: )的函数关系如图,则两车先后两次相遇的间隔时间是( )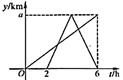 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 若一次函数 y=kx+2 的函数值y随自变量x增大而增大,则实数k的取值范围是.14. 已知 ,当分别取1,2,3,……,2020时,所对应y值的总和是.15. 如图,折叠矩形纸片ABCD , 使点B的对应点E落在CD边上,GH为折痕,已知 , .当折痕GH最长时,线段BH的长为 .
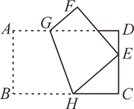 16. 如图,某港口P位于东西方向的海岸线上,甲、乙轮船同时离开港口,各自沿一固定方向航行,甲、乙轮船每小时分别航行12海里和16海里,1小时后两船分别位于点A,B处,且相距20海里,如果知道甲船沿北偏西 方向航行,则乙船沿方向航行.
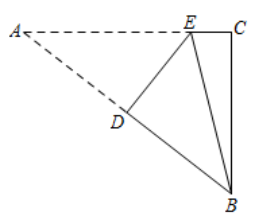
16. 如图,某港口P位于东西方向的海岸线上,甲、乙轮船同时离开港口,各自沿一固定方向航行,甲、乙轮船每小时分别航行12海里和16海里,1小时后两船分别位于点A,B处,且相距20海里,如果知道甲船沿北偏西 方向航行,则乙船沿方向航行.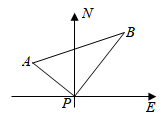 17. 人们把 这个数叫做黄金分割数,著名数学家华罗庚优选法中的 法就应用了黄金分割数.设 , ,则 ,记 , ,…, .则 .18. 如图,一次函数 与坐标轴分别交于 , 两点,点 , 分别是线段 , 上的点,且 , ,则点 的标为.
17. 人们把 这个数叫做黄金分割数,著名数学家华罗庚优选法中的 法就应用了黄金分割数.设 , ,则 ,记 , ,…, .则 .18. 如图,一次函数 与坐标轴分别交于 , 两点,点 , 分别是线段 , 上的点,且 , ,则点 的标为.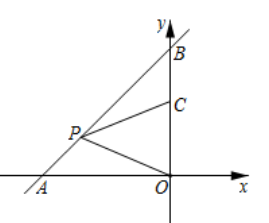
三、解答题
-
19. 计算(1)、(2)、(3)、(4)、20. 已知2a+3的立方根是3,a+b﹣1的算术平方根是4,c是 的整数部分.(1)、求a,b,c的值.(2)、求a﹣4b+3c的平方根.21. 如图所示,在平面直角坐标系中,已知 、 、 .
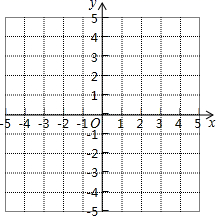
( 1 )在平面直角坐标系中画出 ,则 的面积是_▲_;
( 2 )若点D与点C关于y轴对称,则点D的坐标为_▲_;
( 3 )已知P为x轴上一点,若 的面积为4,求点P的坐标.
22. 十一国庆节,某校各班都在开展丰富多彩的庆祝活动,八年级(1)班开展了手工制作竞赛,每个同学都在规定时间内完成一件手工作品.武玥同学在制作手工作品的第一、二个步骤是: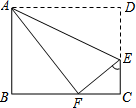
①先裁下了一张长 ,宽 的长方形纸片 ;
②如图,将纸片沿着直线 折叠,点 恰好落在 边上的 处.
请你根据①②步骤计算 , 的长.