黑龙江省哈尔滨市宾县一高2021-2022学年高二上学期数学第一次月考试卷
试卷更新日期:2021-10-22 类型:月考试卷
一、选择题(每题5分)
-
1. 已知正四棱柱 中, 为 中点,则异面直线 与 所成的角的余弦值为( )A、 B、 C、 D、2. 在平行六面体 中, 且 ,求 的长( )A、 B、 C、 D、3. 过直线 和 的交点,且与 垂直的直线方程是( )A、 B、 C、 D、4. 设 , ,若直线 与线段AB有交点,则a的取值范围是( )A、 B、 C、 D、5. 在三棱锥 中, 底面ABC, , , ,则点C到平面PAB的距离是( )
A、 B、 C、 D、6. 已知四边形ABCD中, , , ,若 平面ABCD,且 ,则点P到直线BC的距离为( )
A、 B、 C、 D、57. 已知函数 ( ,且 )恒过定点A.若直线 过点A,其中m、n是正实数,则 的最小值是( )A、 B、 C、 D、58. 若直线 与曲线 有公共点,则 的取值范围是( )A、 B、 C、 D、9. 如图,在正方体 中,O是AC的中点,点P在线段 上,若直线OP与平面 所成的角为 ,则 的取值范围是( )
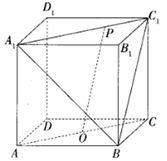 A、 B、 C、 D、10. 在平面直角坐标系 中, 和 是圆 上的两点,且 ,点 ,则 的取值范围是A、 B、 C、 D、11. 下列结论不正确的是( )A、若直线 和 的斜率相等,则 B、经过点 且在 轴和 轴上截距都相等的直线方程为 C、直线 的倾斜角 的取值范围是 D、“ ”是“直线 与直线 互相垂直”的充要条件12. 瑞士著名数学家欧拉在1765年提出定理:三角形的外心、重心、垂心位于同一直线上,这条直线被后人称为三角形的“欧拉线”.若 满足 ,顶点 , ,且其“欧拉线”与圆 相切,则下列结论正确的是( )A、圆 上的点到原点的最大距离为 B、圆 上存在三个点到直线 的距离为 C、若点 在圆 上,则 的最小值是 D、若圆 与圆 有公共点,则 ,
A、 B、 C、 D、10. 在平面直角坐标系 中, 和 是圆 上的两点,且 ,点 ,则 的取值范围是A、 B、 C、 D、11. 下列结论不正确的是( )A、若直线 和 的斜率相等,则 B、经过点 且在 轴和 轴上截距都相等的直线方程为 C、直线 的倾斜角 的取值范围是 D、“ ”是“直线 与直线 互相垂直”的充要条件12. 瑞士著名数学家欧拉在1765年提出定理:三角形的外心、重心、垂心位于同一直线上,这条直线被后人称为三角形的“欧拉线”.若 满足 ,顶点 , ,且其“欧拉线”与圆 相切,则下列结论正确的是( )A、圆 上的点到原点的最大距离为 B、圆 上存在三个点到直线 的距离为 C、若点 在圆 上,则 的最小值是 D、若圆 与圆 有公共点,则 ,二、填空题(每题5分)
-
13. 若直线 与 互相平行,则 的值为;14. 若过点 与 的直线的倾斜角为钝角,则实数a的取值范围15. 过点 作圆 的两条切线,切点分别是A,B,则直线AB的方程为.16. 如图,在四棱锥 中, 平面 , , , ,已知 是四边形 内部一点,且二面角 的平面角大小为 ,则 的面积的取值范围是.

三、解答题
-
17. 已知直线l:(a+1)x+y+2-a=0(a∈R).(1)、若直线l在两坐标轴上的截距相等,求直线l的方程;(2)、当O(0,0)点到直线l的距离最大时,求直线l的方程.18. 已知圆C过 两点,且圆心C在直线 上.(1)、求圆C的方程;(2)、若直线 与圆C相交于M,N两点,求弦 的长度.19. 如图,在多面体ABCDE中, 平面ABC,点D到平面ABC的距离为2, 是正三角形, , .
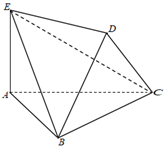 (1)、证明: ;(2)、求直线CE与平面BED所成角的正弦值.20. 如图,在四棱锥 中,底面 是直角梯形, , 平面 , ,点 为 的中点.
(1)、证明: ;(2)、求直线CE与平面BED所成角的正弦值.20. 如图,在四棱锥 中,底面 是直角梯形, , 平面 , ,点 为 的中点. (1)、求证: 平面 ;(2)、若 ,且平面 与平面 所成二面角的平面角为锐角时的余弦值为 ,求四棱锥 的体积.
(1)、求证: 平面 ;(2)、若 ,且平面 与平面 所成二面角的平面角为锐角时的余弦值为 ,求四棱锥 的体积.
