广东省深圳市南山区2021-2022学年九年级上学期数学10月月考试卷

试卷更新日期：2021-10-22 类型：月考试卷

进入出卷网下载

一、选择题(每题3分，共30分)

1. 已知xy=mn，则把它改写成比例式后，错误的是（　　）

A、 $\frac{x}{n} = \frac{m}{y}$ B、 $\frac{y}{m} = \frac{n}{x}$ C、 $\frac{x}{m} = \frac{y}{n}$ D、 $\frac{x}{m} = \frac{n}{y}$

查看试题解析
2. 用配方法解一元二次方程x²-8x+5=0，将其化成(x+a)²=b的形式，则变形正确的是（ )

A、(x - 4)²=11 B、(x-4)²=21 C、(x -8)²=11 D、(x+4)²=11

查看试题解析
3. 九（1）班从小华、小琪、小明、小伟四人中随机抽出2人参加学校举行的乒乓球双打比赛，每人被抽到的可能性相等，则恰好抽到小华和小明的概率是（ )

A、 $\frac{1}{4}$ B、 $\frac{1}{5}$ C、 $\frac{1}{6}$ D、 $\frac{1}{12}$

查看试题解析
4. 下列命题中错误的是（）

A、平行四边形的对边相等　 B、两组对边分别相等的四边形是平行四边形 C、矩形的对角线相等　　　 D、对角线相等的四边形是矩形

查看试题解析
5. 已知关于x的方程mx²-2x+1=0有两个不相等的实数根，则m的取值范围是（）

A、m<1 B、m>1 C、m<1且m≠0 D、m>1且m≠0

查看试题解析
6. 如图，在平行四边形ABCD中，用直尺和圆规作∠BAD的平分线AG交BC于点E，若BF=6，AB=5，则 AE的长为（）

A、10 B、8 C、6 D、4

查看试题解析
7. 如图，在菱形ABCD中，M，N分别在AB，CD上，且 AM=CN，MN与 AC交于点O，连接BO.若∠DAC=28°，则么∠OBC的度数为（）

A、28° B、52° C、62° D、72°

查看试题解析
8. 九年级（5）班文学小组在举行的图书共享仪式上互赠图书，每个同学都把自己的图书向本组其他成员赠送一本，全组共互赠了132本图书，如果设全组共有x名同学，依题意，可列出的方程是（）

A、x（x+1）=132 B、x (x-1)=132 C、2x（x+1）=132 D、 $\frac{1}{2}$ x(x+1）=132

查看试题解析
9. 定义：cx²+bx+a=0是一元二次方程ax²+bx+c=0的倒方程，下列四个结论中，错误的是（）

A、如果x=2是×²+2x+c=0的倒方程的解，则c= $\frac{5}{4}$ B、如果ac<0，那么这两个方程都有两个不相等的实数根 C、如果一元二次方程ax²-2x+c=0无解，则它的倒方程也无解 D、如果一元二次方程ax²-2x+c=0有两个不相等的实数根，则它的倒方程也有两个不相等的实数根

查看试题解析
10. 如图，正方形 ABCD的边长为2，点E从点A出发沿着线段AD向点D运动(不与点A，D重合)，同时点F从点D出发沿着线段DC向点C运动(不与点D，C重合，点E与点F的运动速度相同．BE与AF相交于点G，H为BF中点、则有下列结论：
①∠BGF是定值；②FB平分∠AFC：③当E运动到AD中点时，GH= $\frac{\sqrt{5}}{2}$ ：④当AG+BG= $\sqrt{6}$ 时，四边形GEDF的面积是 $\frac{1}{2}$ ，其中正确的是（ )

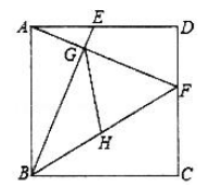A、①②④ B、①②③ C、①③④ D、②③④

查看试题解析

二、填空题(每题3分，共15分)

11. 已知 $\frac{a}{b} = 2$ ，那么 $\frac{a + b}{b} =$ 。

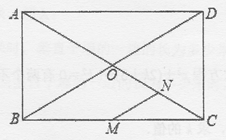
查看试题解析
12. 某地区为估计该地区黄羊的只数，先捕捉20只黄羊给它们分别作上记号然后放还，带有标记的黄羊完全混合于黄羊群后，第二次捕捉40只黄羊，发现其中有2只有标记.从而估计这个地区有黄羊只。

查看试题解析
13. 如图，矩形ABCD中，AC，BD交于点O，M，N分别为BC，OC的中点，若MN=3，则BD=.

查看试题解析
14. 一元二次方程x²＋4x-2=0的两根为m、n，则m²+5m +n的值是.

查看试题解析
15. 如图，在Rt△ABC中，∠ACB=90° ，AC=6，BC=8，AD平分∠CAB交BC于D点，E，F分别是AD，AC上的动点.则CE+ EF的最小值为.

查看试题解析

三、解答题（共55分，其中16题12分，17题5分，18题7分，19题7分，20题7分，21题8分，22题9分)

16. 解方程

(1)、（x-3)²=4.

(2)、x(x-4）=x-4.

(3)、4（x+2）²-9(x-3)²=0.

(4)、2x²+4x-3=0.

查看试题解析
17. 为庆祝中国共产党建党100周年，某校组织七、八、九年级学生参加了“颂党恩，跟党走”作文大赛，该校对参赛作文分年级进行了统计，并绘制了图1和图2不完整的统计图.

请根据图中信息回答下面的问题：

(1)、参赛作文的篇数共篇；

(2)、图中：m= ，扇形统计图中九年级所对应的圆心角度数为。

(3)、把条形统计图补充完整；

(4)、经过评审，全校共有4篇作文获得特等奖，其中有一篇来自七年级，学校准备从特等奖作文中选取2篇刊登在学校校报上，请用树状图或列表法求七年级特等奖作文被刊登在校报上的概率.

查看试题解析
18. 已知关于x的一元二次方程x²+(2k＋3)x+k=0有两个不相等的实数根x₁ ， x₂.

(1)、求k的取值范围；

(2)、若 $\frac{1}{x_{1}} + \frac{1}{x_{2}} = - 1$ ，求k的值.

查看试题解析
19. 如图，在四边形ABCD中， $∠ B A C = 90^{°}$ ，E是BC的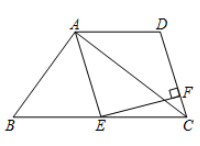中点， $A D / / B C$ ， $A E / / D C$ ， $E F ⊥ C D$ 于点F.

(1)、求证：四边形AECD是菱形；

(2)、若 $A B = 6$ ， $B C = 10$ ，求EF的长.

查看试题解析
20. 某服装厂生产一批服装，2019年该类服装的出厂价是200元/件，2020年，2021年连续两年改进技术，降低成本，2021年该类服装的出厂价调整为162元/件．

(1)、这两年此类服装的出厂价下降的百分比相同，求平均下降率．

(2)、2021年某商场从该服装厂以出厂价购进若干件此类服装，以200元/件销售时，平均每天可销售20件．为了减少库存，商场决定降价销售．经调查发现，单价每降低5元，每天可多售出10件，如果每天盈利1150元，单价应降低多少元?

查看试题解析
21. ①对于任意实数α和b，都有(a-b)²≥0，∴a²- 2ab+b²≥0，于是得到a²+b²≥2ab，当且仅当a=b时，等号成立.
②任意一个非负实数都可写成一个数的平方的形式。即：如果a≥0，则 $a = {(\sqrt{a})}^{2}$ 如： $2 = {(\sqrt{2})}^{2}$ ， $3 = {(\sqrt{3})}^{2}$ 等.

例：已知a>0，求证： $a + \frac{1}{2 a} \geq \sqrt{2}$

证明：∵a>0， $∴ a + \frac{1}{2 a} = {(\sqrt{a})}^{2} + {(\frac{1}{\sqrt{2} a})}^{2} \geq 2 \times \sqrt{a} \times \frac{1}{\sqrt{2} a} = \sqrt{2}$

$∴ a + \frac{1}{2 a} \geq \sqrt{2}$

当且仅当a= $\frac{\sqrt{2}}{2}$ 时，等号成立。

请解答下列问题：某园艺公司准备围建一个矩形花圃，其中一边靠墙（墙足够长)，另外三边用篱笆围成(如图所示)．设垂直于墙的一边长为x米.

(1)、若所用的篱笆长为36米，那么：
①当花圃的面积为144平方米时，垂直于墙的一边的长为多少米?

②设花圃的面积为S米² ，求当垂直于墙的一边的长为多少米时，这个花圃的面积最大?并求出这个最大面积；

(2)、若要围成面积为200平方米的花圃，需要用的篱笆最少是多少米?

查看试题解析
22. 如图，在平面直角坐标系中，直线l₁： $y = - \frac{2}{3} x + 4$ 分别交x、y轴于B、A两点，将△AOB沿直线l₂： $y = 2 x - \frac{9}{2}$ 折叠，点B落在y细的点C处.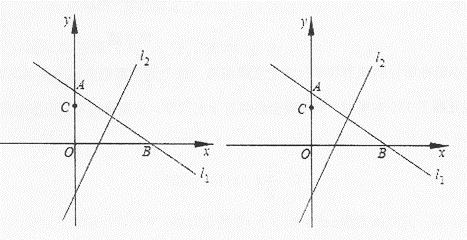

(1)、点C的坐标为：

(2)、若点D沿射线BA运动，连接OD，当△CDB 与△CDO面积相等时，求直线OD的解析式；

(3)、在（2）的条件下，当点D在第一象限时，沿x轴平移直线OD，分别交x，y轴于点E，F，在平面直角坐标系中，是否存在点M(m，3)和点P，使四边形EFMP为正方形?若存在，求出点P的坐标；若不存在，说明理由.

查看试题解析