广西贵港市2020-2021学年度高二上学期理数期末考试试卷
试卷更新日期:2021-10-21 类型:期末考试
一、单选题
-
1. 已知平面 的法向量分别为 且 则 ( )A、 B、-4 C、4 D、82. 设一组样本数据 的方差为 则数据 的方差为( )A、2.5 B、5 C、10 D、203. 2020年以来,网络直播行业迎来新的发展机遇,直播带货模式成为企业的“标配”.由中国互联网络信息中心( )第45次《中国互联网络发展状况统计报告》数据得到如图所示的统计图.2020年12月我国网络直播用户规模达5.60亿,占整体手机网民的62.0%.

根据以上信息,下列说法不正确的是( )
A、2018-2020年我国网络直播用户一直保持增长态势 B、2020年我国手机网民未超过9亿 C、2020年底我国网络直播用户规模较2018年底增长1.63亿 D、2016-2020年我国网络直播用户规模和使用率变化的趋势一致4. 现有下列命题:①若 则 ②若 则 ③命题“ “的否定是” ".其中真命题共有( )
A、0个 B、1个 C、2个 D、3个5. 已知双曲线 有一条渐近线与直线 平行,则该双曲线的离心率为( )A、 B、 C、 D、6. 若某商场的会员只用现金支付的概率为 ,既用现金支付也用非现金支付的概率为 则只用非现金支付的概率为( )A、 B、 C、 D、7. 如图,在长方体 中, 是线段 上一点,且 ,若 ,则 ( ) A、 B、 C、 D、18. 执行如图所示的程序框图,输出的点都在函数( )
A、 B、 C、 D、18. 执行如图所示的程序框图,输出的点都在函数( )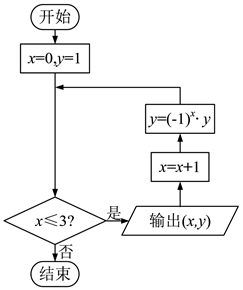 A、 的图象上 B、 的图象上 C、 的图象上 D、 的图象上9. 已知 则“ ”是“ ”的( )A、必要不充分条件 B、充分不必要条件 C、充要条件 D、既不充分也不必要条件10. 在某球内随机放人 个点,恰有 个点落人该球的内接正方体内,则 的近似值为( )A、 B、 C、 D、11. 设 分别是椭圆 的左、右焦点,O为坐标原点,点 在 上且 ,则 的面积为( )A、 B、8 C、7 D、1612. 如图,已知抛物线 ,圆 ,过圆心 的直线 与抛物线和圆依次交于点 , , , ,则 ( )
A、 的图象上 B、 的图象上 C、 的图象上 D、 的图象上9. 已知 则“ ”是“ ”的( )A、必要不充分条件 B、充分不必要条件 C、充要条件 D、既不充分也不必要条件10. 在某球内随机放人 个点,恰有 个点落人该球的内接正方体内,则 的近似值为( )A、 B、 C、 D、11. 设 分别是椭圆 的左、右焦点,O为坐标原点,点 在 上且 ,则 的面积为( )A、 B、8 C、7 D、1612. 如图,已知抛物线 ,圆 ,过圆心 的直线 与抛物线和圆依次交于点 , , , ,则 ( ) A、2 B、4 C、6 D、8
A、2 B、4 C、6 D、8二、填空题
-
13. 某班有男生40人,女生30人,现用分层抽样的方法从中抽取14人参加一项活动,则抽取的男生的人数为.14. 如图所示的程序的输出结果是.
 15. 已知 为正方体 外接球的球心, 为棱 的中点,则异面直线 与 所成角的余弦值为.16. 过双曲线 : 的右焦点 作圆 : 的切线,此切线与 的右支交于 , 两点,则 .
15. 已知 为正方体 外接球的球心, 为棱 的中点,则异面直线 与 所成角的余弦值为.16. 过双曲线 : 的右焦点 作圆 : 的切线,此切线与 的右支交于 , 两点,则 .三、解答题
-
17. 石漠化,是指因水土流失而导致地表土壤损失,基岩裸露,土地丧失农业利用价值和生态环境退化的现象,某地区实施植树造林,不断强化荒漠化地区生态保护和修复,全力推进石漠化综合治理,从 年该地区每年植树造林面积的数据如下表所示.
年份
2016
2017
2018
2019
2020
年份代码
1
2
3
4
5
(亩)
0.5
0.6
0.7
0.8
1
附:线性回归方程 中斜率和截距的最小二乘法估计公式分别为: , , , .
(1)、求 关于 的线性回归方程;(2)、试问到2021年该地区植树造林的总面积能否超过4.6亩?18. 如图,在四棱锥 中,平面 平面 ,底面 为正方形, ,点 是 的中点. (1)、证明: 平面 .(2)、已知点 是边 上靠近 点的三等分点,求平面 与平面 所成锐二面角的余弦值.19. “绿水青山就是金山银山,坚持人与自然和谐共生”的理念越来越深入人心,现已形成了全民自觉参与,造福百姓的良性循环.据此,某网站推出了关于生态文明建设进展情况的调查,调查数据表明,环境治理和保护问题仍是百姓最为关心的热点.现从参与关注生态文明建设的人群中随机选出100人,并将这100人按年龄分为第1组 ,第2组 ,第3组 ,第4组 ,如图所示,已知区间 , , , 上的频率依次成等差数列.
(1)、证明: 平面 .(2)、已知点 是边 上靠近 点的三等分点,求平面 与平面 所成锐二面角的余弦值.19. “绿水青山就是金山银山,坚持人与自然和谐共生”的理念越来越深入人心,现已形成了全民自觉参与,造福百姓的良性循环.据此,某网站推出了关于生态文明建设进展情况的调查,调查数据表明,环境治理和保护问题仍是百姓最为关心的热点.现从参与关注生态文明建设的人群中随机选出100人,并将这100人按年龄分为第1组 ,第2组 ,第3组 ,第4组 ,如图所示,已知区间 , , , 上的频率依次成等差数列. (1)、分别求出区间 , , 上的频率;(2)、现从年龄在 及 的人群中按分层抽样抽取5人,再从中选3人作为生态文明建设知识宣讲员,用 表示抽到作为宣讲员的年龄在 的人数, 表示抽到作为宣讲员的年龄在 的人数,求满足 的概率.
(1)、分别求出区间 , , 上的频率;(2)、现从年龄在 及 的人群中按分层抽样抽取5人,再从中选3人作为生态文明建设知识宣讲员,用 表示抽到作为宣讲员的年龄在 的人数, 表示抽到作为宣讲员的年龄在 的人数,求满足 的概率.