浙江省浙江省绍兴市诸暨市浣江教育共同体2021-2022学年九年级上学期数学9月月考试卷
试卷更新日期：2021-10-21 类型：月考试卷
一、选择题（共10小题）.
-
1. 下列命题中，不正确的是（ ）A、垂直平分弦的直线经过圆心 B、平分弦的直径一定垂直于弦 C、平行弦所夹的两条弧相等 D、垂直于弦的直径必平分弦所对的弧2. 如图，A，B，C是⊙O上三点，∠ACB＝25°，则∠BAO的度数是（ ）
A、55° B、60° C、65° D、70°3. 给定下列图形可以确定一个圆的是（ ）A、已知圆心 B、已知半径 C、已知直径 D、已知三个点4. 如图，CD是⊙O的弦，O是圆心，把⊙O的劣弧沿着CD对折，A是对折后劣弧上的一点，∠CAD＝100°，则∠B的度数是（ ）
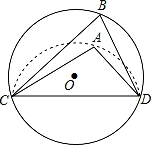A、100° B、80° C、60° D、50°5. 如图，将△ABC放在每个小正方形边长为1的网格中，点A，B，C均落在格点上，用一个圆面去覆盖△ABC，能够完全覆盖这个三角形的最小圆面半径是（ ）
A、 B、 C、2 D、6. 如图，点A为⊙O上一点，OD⊥弦BC于点D，如果∠BAC＝60°，OD＝1，则BC为（ ）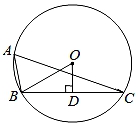
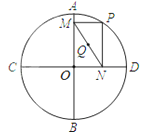
A、 B、2 C、2 D、47.如图，⊙O的半径为2，AB、CD是互相垂直的两条直径，点P是⊙O上任意一点（P与A、B、C、D不重合），经过P作PM⊥AB于点M，PN⊥CD于点N，点Q是MN的中点，当点P沿着圆周转过45°时，点Q走过的路径长为（ ）
A、 B、 C、 D、8. 如图，将△ABC绕点C顺时针旋转得到△EDC，若点A恰好在ED的延长线上，∠BAC＝40°，则∠BAE的度数为（ ）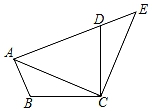
A、80° B、60° C、65° D、70°9. 如图，点A的坐标为A（8，0），点B在y轴正半轴上，且AB＝10，点P是△AOB外接圆上一点，且∠BOP＝45°，则点P的坐标为（ ）
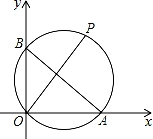A、（7，7） B、（7 ，7 ） C、（5 ，5 ） D、（5，5）10. 计算机处理任务时，经常会以圆形进度条的形式显示任务完成的百分比.下面是同一个任务进行到不同阶段时进度条的示意图：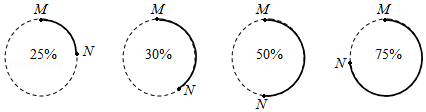
若圆半径为1，当任务完成的百分比为x时，线段MN的长度记为d（x）.下列描述正确的是（ ）
A、d（25%）＝1 B、当x＞50%时，d（x）＞1 C、当x1＞x2时，d（x1）＞d（x2） D、当x1+x2＝100%时，d（x1）＝d（x2）二、填空题（共6小题）
-
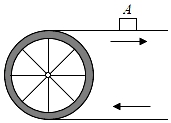
11. ⊙O内一点P到⊙O上的最近点的距离为2，最远点的距离为4，则⊙O的半径为 .12. 如图，已知某一条传送带的转动轮的半径为30厘米.如果该转动轮转动120°，那么传送带上的物品A被传送厘米.（结果保留π）
13. 如图，若干全等正五边形排成环状.图中所示的是前3个正五边形，要完成这一圆环还需 个正五边形.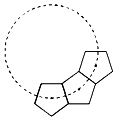
14. 如图，四边形ABCD是菱形，⊙O经过点A、C、D，与BC相交于点E，连接AC、AE.若∠D＝70°，则∠EAC的度数为.
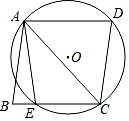15. 如图，已知在扇形AOB中，∠AOB＝90°，半径 ，正方形FCDE的四个顶点分别在 和半径OA、OB上，则CD的长为.
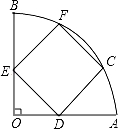16. 如图，AB是⊙O的直径，C、D是⊙O上的两个动点（点C、D不与A、B重合），在运动过程中弦CD始终保持不变，F是弦CD的中点，过点C作CE⊥AB于点E.若CD＝5，AB＝6，则EF的最大值为 ， 此时CE的长度为 .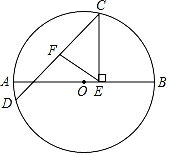
三、解答题（共8小题）
-
17. 如图，⊙O中的弦AB＝CD，AB与CD相交于点E.求证：
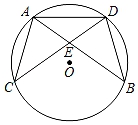(1)、AC＝BD；(2)、CE＝BE.18. 如图：在平面直角坐标系中，网格中每一个小正方形的边长为1个单位长度；已知△ABC.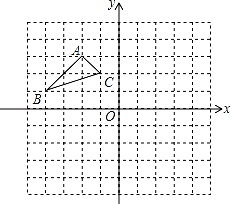
⑴作出△ABC以O为旋转中心，顺时针旋转90°的△A1B1C1；（只画出图形）
⑵作出△ABC关于原点O成中心对称的△A2B2C2；（只画出图形）
⑶在（1）的条件下，求出线段AC扫过的面积.
19. 如图，AB是⊙O的直径，C是半圆上任意一点，连接BC并延长到点D，使得CD＝CB，连接AD，点E是弧 的中点.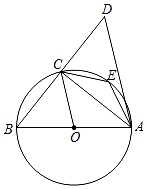
(1)、证明：△ABC≌△ADC.(2)、①当∠E＝°时，△ABD是直角三角形；②当∠D＝°时，四边形OAEC是菱形.
20. 如图，⊙O的直径AB为10厘米，弦AC为6厘米，∠ACB的平分线交⊙O于D.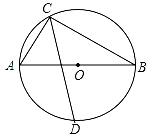
(1)、连接AD，BD，判断△ABD的形状，并说明理由；(2)、求弦CD的长.21. 如图，有一座圆弧形拱桥，桥下水面宽度AB为12m，拱高CD为4m.
(1)、求拱桥的半径；(2)、有一艘宽为5m的货船，船舱顶部为长方形，并高出水面3.4m，则此货船是否能顺利通过此圆弧形拱桥，并说明理由；22. 如图，在平面直角坐标系xOy中，已知点A（1，0），点C是y轴上的动点，线段CA绕着点C逆时针旋转90°至线段CB，连接BO，设点C的纵坐标为m.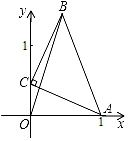
(1)、求点B的坐标（用含m的式子表示）；(2)、求线段BO长度的最小值.23. 如图，四边形ABCD内接于⊙O，AC为直径，AC和BD交于点E，AB＝BC.
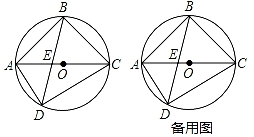(1)、求∠ADB的度数；(2)、过B作AD的平行线，交AC于F，试判断线段EA，CF，EF之间满足的等量关系，并说明理由.24. 阅读下列材料：
问题：如图1，在正方形ABCD内有一点P，PA＝ ，PB＝ ，PC＝1，求∠BPC的度数.
小明同学的想法是：已知条件比较分散，可以通过旋转变换将分散的已知条件集中在一起，于是他将△BPC绕点B逆时针旋转90°，得到了△BP′A（如图2），然后连接PP′.
请你参考小明同学的思路，解决下列问题：
(1)、如图2，△APP′为 ， △BPP′为 ；（填等腰三角形，直角三角形或等腰直角三角形）(2)、如图2，∠BPC的度数为 ；(3)、如图3，若在正六边形ABCDEF内有一点P，且PA＝2 ，PB＝4，PC＝2，则求：①∠BPC的度数；
②正六边形ABCDEF的边长.