浙江省宁波市鄞州区2021-2022学年八年级上学期数学暑期空中课堂学习自我检测试卷

试卷更新日期：2021-10-21 类型：开学考试

进入出卷网下载

一、选择题（每小题3分，共30分）

1. 下列各数：-2，0， $\frac{1}{3}$ ，0.020020002…， $π$ ， $\sqrt{9}$ ，其中无理数的个数是（）

A、4 B、3 C、2 D、1

查看试题解析
2. 下列计算结果正确的有（）
①－2²÷(－2)³＝1②－5÷ $\frac{1}{3}$ × $\frac{3}{5}$ ＝－25③－18÷6÷2＝－6④－1³－(－1)²＝－2

A、1个 B、2个 C、3个 D、4个

查看试题解析
3. 当1<a<2时，代数式|a－2|＋|1－a|的值是（）

A、－1 B、1 C、3 D、－3

查看试题解析
4. 某新型病毒的直径约为0.000 000 823 m ，将0.000 000 823用科学记数法表示为（）

A、8.23×10^－6 B、8.23×10^－7 C、8.23×10⁶ D、8.23×10⁷

查看试题解析
5. 用代入消元法解方程组 ${\begin{array}{l} 3 x + 4 y = 2 ， ① \\ 2 x - y = 5 ② \end{array}$ 使代入后化简比较容易的变形是（）

A、由①得 $x = \frac{2 - 4 y}{3}$ B、由①得 $y = \frac{2 - 3 x}{4}$ C、由②得 $x = \frac{y + 5}{2}$ D、由②得y＝2x－5

查看试题解析
6. 如图，直线m∥n，将一块含45°角的直角三角板ABC按如图方式放置，其中边BC与直线n交于点D.若∠1=25°，则∠2的度数为（）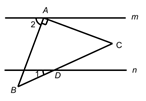

A、60° B、65° C、70° D、75°

查看试题解析
7. 要使多项式2x²－2(7＋3x－2x²)＋mx²化简后不含x的二次项，则m的值是（）

A、2 B、0 C、－2 D、－6

查看试题解析
8. 火车站、机场、邮局等场所都有为旅客提供打包服务的项目．现有一个长、宽、高分别为a、b、c的箱子，按如图所示的方式打包，则打包带的长(不计接头处的长)至少应为（）

A、2a＋2b＋4c B、2a＋4b＋6c C、4a＋4b＋8c D、4a＋6b＋6c

查看试题解析
9. 若x²+ $\frac{1}{2}$ mx+k是一个完全平方式，则k等于（）

A、 $\frac{1}{16} m^{2}$ B、 $\frac{1}{4} m^{2}$ C、 $\frac{1}{3} m^{2}$ D、m²

查看试题解析
10. 设a ， b ， c为互不相等的实数，且 $b = \frac{4}{5} a + \frac{1}{5} c$ ，则下列结论正确的是（）

A、a>b>c B、c>b>a C、a-b=4(b-c) D、a-c=5(a-b)

查看试题解析

二、二、填空题（每小题3分，共18分）

11. －2²－|－2|＋ $\sqrt{\frac{1}{9}}$ ＋(－1)²⁰²¹=.

查看试题解析
12. 如图，AB//CD ， ∠A=25° ， ∠E=80°，则∠C的度数是．

查看试题解析
13. 如图，数轴上表示2， $\sqrt{5}$ 的点分别为C ， B ，点C是AB的中点，则点A表示的数是．

查看试题解析
14. 如图，用边长为1cm的小正方形搭成如下的塔状图形，则第n次所搭图形的周长是cm（结果用含n的代数式表示）.

查看试题解析
15. 一食堂需要购买盒子存放食物，盒子有A，B两种型号，单个盒子的容量和价格如表，现有15升食物需要存放且要求每个盒子要装满.由于A型号盒子正在做促销活动：购买三个及三个以上可一次性返现金4元，则购买盒子所需要最少费用为元.

型号

A

B

单个盒子容量（升)

2

3

单价（元)

5

6

查看试题解析
16. 如图，正方形ABCD、正方形CEFG的一边重合，它们边长分别为a ， b（a<b），则△BDF的面积是．

查看试题解析

三、解答题（第17~19题各6分，第20~22题各8分，第23题10分，共52分）

17. 化简： $(a - 2 b) (a + 2 b) - {(a - 2 b)}^{2} + 8 b^{2}$

查看试题解析
18. 先化简，再求值： $(\frac{x^{2} - 4}{x^{2} - 4 x + 4} - \frac{1}{x - 2}) \cdot \frac{x^{2} - 2 x}{x + 1}$ ，其中x=5.

查看试题解析
19. 如图是由边长为1的小正方形拼成的网格.

(1)、在图1网格中找格点P ，使得AP与AB垂直．

(2)、在图2网格中找格点P ，使得△ABP的面积是3．

(3)、在图3网格中找格点P ，使得PA=PB ．

查看试题解析
20. 如图，数轴上A点对应的数为－5，B点在A点右边，电子蚂蚁甲、乙在B分别以分别以2个单位/秒、1个单位/秒的速度向左运动，电子蚂蚁丙在A以3个单位/秒的速度向右运动.

(1)、若电子蚂蚁丙经过5秒运动到C点，求C点表示的数；

(2)、若它们同时出发，若丙在遇到甲后1秒遇到乙，求B点表示的数。

查看试题解析
21. 如图1所示是一个长2m ，宽2n的长方形，沿图中虚线用剪刀将其均分为四块小长方形，然后按图2的形状拼成一个正方形.

(1)、用两种方法表示图2中阴影部分的面积.

(2)、观察图2，请你写出代数式 ${(m + n)}^{2}$ ， ${(m - n)}^{2}$ ， $m n$ 之间的等量关系式.

(3)、根据(2)中的结论，若 $x + y = - 6$ ， $x y = 2.75$ ，求 $x - y$ 的值.

查看试题解析
22. 某厂用如图甲所示的长方形和正方形纸板做成如图乙所示的A，B，两种长方体形状的无盖纸盒.现有正方形纸板140张，长方形纸板360张，刚好全部用完，问能做成多少个A型盒子？多少个B型盒子？

(1)、根据题意，甲和乙两同学分别列出的方程组如下：甲： ${\begin{matrix} x + 2 y = 140 \\ 4 x + 3 y = 360 \end{matrix}$ ，
乙： ${\begin{matrix} x + y = 140 \\ 4 x + \frac{3}{2} y = 360 \end{matrix}$ ，根据两位同学所列的方程组，请你分别指出未知数 $x ， y$ 表示的意义：甲： $x$ 表示， $y$ 表示；乙： $x$ 表示， $y$ 表示.

(2)、求出做成的A型盒子和B型盒子分别有多少个?

查看试题解析

23. 某通讯公司推出以下收费套餐，小明选择了套餐A ，小王选择了套餐B ，设小明的通话时间为

t_{1}

分钟，小王的通话时间为

t_{2}

分钟；

	月租费（元/月）	不加收通话费时限（分）	超时加收通话费标准（元/分）
套餐A	58	150	0.25
套餐B	88	350	0.20

(1)、请用含

t_{1}

、

t_{2}

的代数式表示小明和小王的通话费用．

(2)、若小明4月份通话时间为390分钟.小王通话费用和小明相同，求小王通话时间．

(3)、若小明和小王5月份通话时间和通话费用都一样，求通话时间.

查看试题解析

型号	A	B
单个盒子容量（升)	2	3
单价（元)	5	6