江苏省南通市新桥中学2021-2022学年九年级上学期数学第二次月考试卷
试卷更新日期:2021-10-21 类型:月考试卷
一、单选题
-
1. 已知 = ,则 的值为( )A、﹣2 B、2 C、﹣ D、2. 在△ABC中,∠C=90°,AC=8,BC=6,则sinB的值是( )A、 B、 C、 D、3. 下列命题中一定错误的是 ( )A、所有的等腰三角形都相似; B、有一对锐角相等的两个直角三角形相似 C、全等的三角形一定相似; D、所有的等边三角形都相似4. 如图,点P在△ABC的边AC上,添加一个条件可判断△ABP∽△ACB,其中添加不正确的是( )
 A、∠ABP=∠C B、∠APB=∠ABC C、 = D、 =5. 如图,已知点E(﹣4,2),点F(﹣1,﹣1),以O为位似中心,把△EFO放大为原来的2倍,则E点的对应点坐标为( )
A、∠ABP=∠C B、∠APB=∠ABC C、 = D、 =5. 如图,已知点E(﹣4,2),点F(﹣1,﹣1),以O为位似中心,把△EFO放大为原来的2倍,则E点的对应点坐标为( )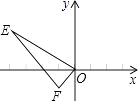 A、(2,﹣1)或(﹣2,1) B、(8,﹣4)或(﹣8,4) C、(2,﹣1) D、(8,﹣4)6. 如图,直线 , 被三条平行线所截,若 , , ,则 的长为( )
A、(2,﹣1)或(﹣2,1) B、(8,﹣4)或(﹣8,4) C、(2,﹣1) D、(8,﹣4)6. 如图,直线 , 被三条平行线所截,若 , , ,则 的长为( ) A、2 B、3 C、6 D、7. 如图,一同学在湖边看到一棵树,他目测出自己与树的距离为20m,树的顶端在水中的倒影距自己5m远,该同学的身高为1.7m,则树高为( )m.
A、2 B、3 C、6 D、7. 如图,一同学在湖边看到一棵树,他目测出自己与树的距离为20m,树的顶端在水中的倒影距自己5m远,该同学的身高为1.7m,则树高为( )m.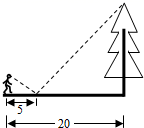 A、3.4 B、5.1 C、6.8 D、8.58. 如图,在菱形ABCD中,DE⊥AB, ,BE=2,则tan∠DBE的值是( )
A、3.4 B、5.1 C、6.8 D、8.58. 如图,在菱形ABCD中,DE⊥AB, ,BE=2,则tan∠DBE的值是( )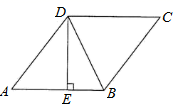 A、 B、2 C、 D、9. 如图,在矩形 中, 于E,设 ,且 , ,则 的长为( )
A、 B、2 C、 D、9. 如图,在矩形 中, 于E,设 ,且 , ,则 的长为( ) A、 B、 C、 D、10. 如图,AB=4,射线BM和AB互相垂直,点D是AB上的一个动点,点E在射线BM上,2BE=DB,作EF⊥DE并截取EF=DE,连接AF并延长交射线BM于点C.设BE=x,BC=y,则y关于x的函数解析式是( )
A、 B、 C、 D、10. 如图,AB=4,射线BM和AB互相垂直,点D是AB上的一个动点,点E在射线BM上,2BE=DB,作EF⊥DE并截取EF=DE,连接AF并延长交射线BM于点C.设BE=x,BC=y,则y关于x的函数解析式是( ) A、y=﹣ B、y=﹣ C、y=﹣ D、y=﹣
A、y=﹣ B、y=﹣ C、y=﹣ D、y=﹣二、填空题
-
11. 在一幅比例尺是1∶6000000的图纸上,量得两地的图上距离是2厘米,则两地的实际距离是千米.12. 如图,直线AB∥CD∥EF,已知AC=3,CE=4,BD=3.6,则DF的长为.
 13. 如图,在▱ABCD中,点E在DC上,若EC:AB=2:3,则S△ECF:S△BAF=.
13. 如图,在▱ABCD中,点E在DC上,若EC:AB=2:3,则S△ECF:S△BAF=. 14. 在△ABC中,若∠A , ∠B满足|cosA- |+(sinB- )2=0,则∠C= .15. 如图, 是 的直径,点C和点D是 上位于直径 两侧的点,连结 , , , ,若 的半径是 , ,则 的值是.
14. 在△ABC中,若∠A , ∠B满足|cosA- |+(sinB- )2=0,则∠C= .15. 如图, 是 的直径,点C和点D是 上位于直径 两侧的点,连结 , , , ,若 的半径是 , ,则 的值是. 16. 如图, 是等腰直角三角形,且 , 是 的中线,过点C作 交 于点F,交 于点E,则 的长为.
16. 如图, 是等腰直角三角形,且 , 是 的中线,过点C作 交 于点F,交 于点E,则 的长为. 17. 如图,在△ABC中,CD⊥AB于点D.若AD=2,BC=8,CD=6,则△ABC的外接圆的半径为
17. 如图,在△ABC中,CD⊥AB于点D.若AD=2,BC=8,CD=6,则△ABC的外接圆的半径为 18. 如图,在等腰 中, ,过点B作 于点B,交过点A直线 交于点D,且 , ,连接 ,若 , 时,则 .
18. 如图,在等腰 中, ,过点B作 于点B,交过点A直线 交于点D,且 , ,连接 ,若 , 时,则 .
三、解答题
-
19. 计算:(1)、tan2 45°-tan 60°cos 30°(2)、20. 如图,AB∥CD,AD、BC相交于点O,若OA=2,OD=4,AB=3.
 (1)、求证:△AOB∽△DOC;(2)、求CD的长度.21. 如图,天空中有一个静止的广告气球C,从地面A点测得C点的仰角为45°,从地面B点测得C点的仰角为60°.已知AB=20m,点C和直线AB在同一铅垂平面上,求气球离地面的高度(结果保留根号).
(1)、求证:△AOB∽△DOC;(2)、求CD的长度.21. 如图,天空中有一个静止的广告气球C,从地面A点测得C点的仰角为45°,从地面B点测得C点的仰角为60°.已知AB=20m,点C和直线AB在同一铅垂平面上,求气球离地面的高度(结果保留根号). 22. 如图,在△ABC中,∠B=90°,点D,E在BC上,且AB=BD=DE=EC,求证:
22. 如图,在△ABC中,∠B=90°,点D,E在BC上,且AB=BD=DE=EC,求证: (1)、△ADE∽△CDA;(2)、∠1+∠2+∠3=90°23. 如图,在Rt△ABC中,∠BAC=90°,AB=AC,E,D分别是BC,AC上的点,且∠AED=45°
(1)、△ADE∽△CDA;(2)、∠1+∠2+∠3=90°23. 如图,在Rt△ABC中,∠BAC=90°,AB=AC,E,D分别是BC,AC上的点,且∠AED=45°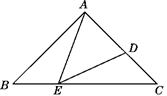 (1)、求证△ABE∽△ECD;(2)、若AB=4,BE= ,求CD的长.24. 如图, 为 的直径, 为 上两点,且 为弧 的中点,过点 作 的垂线,交 的延长线于点 ,交 的延长线于点 ,连结
(1)、求证△ABE∽△ECD;(2)、若AB=4,BE= ,求CD的长.24. 如图, 为 的直径, 为 上两点,且 为弧 的中点,过点 作 的垂线,交 的延长线于点 ,交 的延长线于点 ,连结 (1)、求证: 是 的切线;(2)、当 时,求 的长.25. 已知锐角△ABC中,边BC长为12,高AD长为8.(1)、如图,矩形EFGH的边GH在BC边上,其余两个顶点E、F分别在AB、AC边上,EF交AD于点K.
(1)、求证: 是 的切线;(2)、当 时,求 的长.25. 已知锐角△ABC中,边BC长为12,高AD长为8.(1)、如图,矩形EFGH的边GH在BC边上,其余两个顶点E、F分别在AB、AC边上,EF交AD于点K.①求的值;
②设EH=x,矩形EFGH的面积为S,求S与x的函数关系式,并求S的最大值;
 (2)、若AB=AC,正方形PQMN的两个顶点在△ABC一边上,另两个顶点分别在△ABC的另两边上,直接写出正方形PQMN的边长.26. 如果,已知△ABC , A(0,﹣4),B(﹣2,0),C(4,0).
(2)、若AB=AC,正方形PQMN的两个顶点在△ABC一边上,另两个顶点分别在△ABC的另两边上,直接写出正方形PQMN的边长.26. 如果,已知△ABC , A(0,﹣4),B(﹣2,0),C(4,0).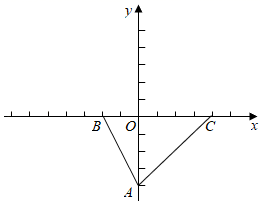 (1)、求sin∠BAC的值.(2)、若点P在y轴上,且△POC与△AOB相似,请直接写出点P的坐标.(3)、已知点M在y轴上,如果∠OMB+∠OAB=∠ACB , 求点M的坐标.
(1)、求sin∠BAC的值.(2)、若点P在y轴上,且△POC与△AOB相似,请直接写出点P的坐标.(3)、已知点M在y轴上,如果∠OMB+∠OAB=∠ACB , 求点M的坐标.