江苏省连云港市灌云县西片2021-2022学年九年级上学期数学第一次月考试卷

试卷更新日期：2021-10-21 类型：月考试卷

进入出卷网下载

一、单选题

1. 若关于x的一元二次方程为 $a x^{2} + b x + 5 = 0 (a \neq 0)$ 的解是 $x = 1$ ，则 $2021 - a - b$ 的值是（）

A、2016 B、2020 C、2025 D、2026

查看试题解析
2. 已知关于x的一元二次方程 $(a - 1) x^{2} - 4 x - 1 = 0$ 有两个实数根，则a的取值范围是（）

A、 $a \geq - 4$ B、 $a > - 3$ C、 $a \geq - 3$ 且 $a \neq 1$ D、 $a > - 3$ 且 $a \neq 1$

查看试题解析
3. 一元二次方程x²＝3x的根是（）

A、3 B、3或﹣3 C、0或3 D、 $\sqrt{3}$ 或 $- \sqrt{3}$

查看试题解析
4. 平面直角坐标系中，⊙O的圆心在原点，半径为5，则点 $P (0 ， 4)$ 与⊙O的位置关系是（　　）

A、点P在⊙O内 B、点P在⊙O上 C、点P在⊙O外 D、无法确定

查看试题解析
5. 如图，AD是△ABC的外接圆⊙O的直径，若∠BCA＝50°，则∠BAD＝（　　）

A、30° B、40° C、50° D、60°

查看试题解析
6. 在今年举办的东京奥运会上，杨倩在女子10米气步枪决赛中夺得冠军，为中国代表团揽入首枚金牌，随后杨倩同款“小黄鸭”发卡在电商平台上爆单，该款发卡在某电商平台上7月24日的销量为5000个，7月25日和7月26日的总销量是22500个.若月25日和26日较前一天的增长率均为x，则满足的方程是（　　）

A、5000（1+x）²＝22500 B、5000（1﹣x）²＝22500 C、5000+5000（1+x）+5000（1+x）²＝22500 D、5000（1+x）+5000（1+x）²＝22500

查看试题解析

二、填空题

7. 一元二次方程3x²﹣x+9＝0的一次项是.

查看试题解析
8. 方程 $3 x^{2} - 8 x - 3 = 0$ 配成 (x-m)²=n 的形式为.

查看试题解析
9. 直角三角形的两直角边长分别为8和6，则此三角形的外接圆半径是.

查看试题解析
10. 如果一个直角三角形的三边长为三个连续偶数，则它的周长为.

查看试题解析
11. 如图，AB是⊙O的直径，点C在⊙O上，CD⊥AB，垂足为D，已知CD=4，OD=3，求AB的长是.

查看试题解析
12. 如图，点A、B、C、D在⊙O上， $\overset{⌢}{A B} = \overset{⌢}{D C}$ ，则ACBD（填“＞”“＜”或“=”）

查看试题解析
13. 若点O是等腰△ABC的外心，且∠BOC＝60°，底边BC＝8，则S_△ABC＝.

查看试题解析
14. 解方程（x﹣1）²﹣5（x﹣1）+4＝0时，我们可以将x﹣1看成一个整体，设x﹣1＝y，则原方程可化为y²﹣5y+4＝0，解得y₁＝1，y₂＝4.当y＝1时，即x﹣1＝1，解得x＝2；当y＝4时，即x﹣1＝4，解得x＝5，所以原方程的解为：x₁＝2，x₂＝5.则利用这种方法求得方程（2x+5）²﹣4（2x+5）+3＝0的解为.

查看试题解析

三、解答题

15. 解下列一元一次方程：

(1)、x²+x＝0；

(2)、x²﹣4x﹣7＝0.

查看试题解析
16. 已知关于 $x$ 的一元二次方程 $x^{2} - 2 x + k + 2 = 0$ .

(1)、若 $k = - 6$ ，求此方程的解；

(2)、若该方程无实数根，求 $k$ 的取值范围.

查看试题解析
17. 如图，在平面直角坐标系中，A（0，4）、B（4，4）、C（6，2）.

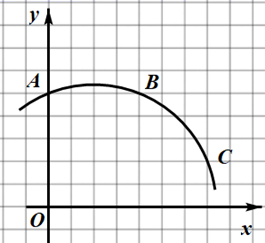(1)、经过A、B、C三点的圆弧所在圆的圆心M的坐标为；

(2)、这个圆的半径为；

(3)、直接判断点D（5，﹣2）与⊙M的位置关系.点D（5，﹣2）在⊙M（填内、外、上）.（并说明理由）

查看试题解析
18. 先阅读下面的内容，再解决问题.
例题：若m²+2mn+2n²﹣6n+9＝0，求m和n的值.

解：∵m²+2mn+2n²﹣6n+9＝0，

∴m²+2mn+n²+n²﹣6n+9＝0，

∴（m+n）²+（n﹣3）²＝0，

∴m+n＝0，n﹣3＝0，

∴m＝﹣3，n＝3.

问题：

(1)、若x²+2y²+2xy+4y+4＝0，求y^x的值.

(2)、已知△ABC的三边长分别为a，b，c（其中a，b，c均不相等），满足a²+b²＝6a+8b﹣25，且c是△ABC中最长的边，求c的取值范围.

查看试题解析
19. 某商场销售某种冰箱，每台进货价为2500元，标价为3000.

(1)、若商场连续两次降价，每次降价的百分率相同，最后以2430元售出，求每次降价的百分率；

(2)、市场调研表明：当每台售价为2900元时，平均每天能售出8台；当每台售价每降50元时，平均每天就能多售出4台.若商场要使这种冰箱的销售利润平均每天达到5000元，则每台冰箱的售价应为多少元？

查看试题解析
20. 方程是含有未知数的等式，使等式成立的未知数的值称为方程的“解”.方程的解的个数会有哪些可能呢？

(1)、根据“任何数的偶数次幂都是非负数”可知：关于x的方程x²+1＝0的解的个数为；

(2)、根据“几个数相乘，若有因数为0，则乘积为0”可知方程（x+1）（x﹣2）（x﹣3）＝0的解不止一个，直接写出这个方程的所有解；

(3)、结合数轴，探索方程|x+1|+|x﹣3|＝4的解的个数；（写出结论，并说明理由）

(4)、进一步可以发现，关于x的方程|x﹣m|+|x﹣3|＝2m+1（m为常数）的解的个数随着m的变化而变化…请你继续探索，直接写出方程的解的个数与对应的m的取值情况.

查看试题解析