江苏省扬州市江都区2021年数学中考一模试卷
试卷更新日期:2021-10-21 类型:中考模拟
一、单选题
-
1. 实数2021的相反数是( )A、2021 B、-2021 C、 D、2. 下列运算正确的是( )A、 B、 C、 D、3. 关于 的一元二次方程 的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、无实数根 D、不能确定4. 下列各统计量中,表示一组数据波动程度的量是( )A、平均数 B、众数 C、方差 D、频率5. 下列三棱柱展开图错误的是( )A、
 B、
B、 C、
C、 D、
D、 6.
6.如图,AB∥CD,∠B=68°,∠E=20°,则∠D的度数为( )
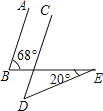 A、28° B、38° C、48° D、88°7. 如图,把直角三角形ABO放置在平面直角坐标系中,已知 ,B点的坐标为 ,将 沿着斜边AB翻折后得到 ,则点C的坐标是( )
A、28° B、38° C、48° D、88°7. 如图,把直角三角形ABO放置在平面直角坐标系中,已知 ,B点的坐标为 ,将 沿着斜边AB翻折后得到 ,则点C的坐标是( )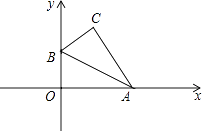 A、 B、 C、 D、8. 如图, 的顶点 在 轴上,横坐标相等的顶点 、 分别在 与 图象上,则 的面积为( )
A、 B、 C、 D、8. 如图, 的顶点 在 轴上,横坐标相等的顶点 、 分别在 与 图象上,则 的面积为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 2021年2月24日6时29分,我国首次火星探测任务“天问一号”探测器成功实施第三次近火制动,进入近火点280千米、远火点59000千米、周期2个火星日的火星停泊轨道.数据59000用科学记数法表示为.10. 因式分解:3a2-6a+3=.11. 若式子在实数范围内有意义,则x的取值范围是 .
12. 若 ,则 .13. 如图,在一次游园活动中,数学小组制作了一面“赵爽弦图锣”,其中 , , ,小明蒙上眼睛用棍子击中了锣面,他击中阴影部分的概率是. 14. 用一个圆心角为240°,半径为3的扇形作一个圆锥的侧面,这个圆锥的底面圆的半径为 .15. 已知 为锐角,且 ,则 .16. 如图,菱形 的对角线 , 相交于点 ,过点 作 于点 ,连接 ,若 , ,则 的长为.
14. 用一个圆心角为240°,半径为3的扇形作一个圆锥的侧面,这个圆锥的底面圆的半径为 .15. 已知 为锐角,且 ,则 .16. 如图,菱形 的对角线 , 相交于点 ,过点 作 于点 ,连接 ,若 , ,则 的长为. 17. 如图,四边形 是 的内接四边形,若 , , , .则 的长为.
17. 如图,四边形 是 的内接四边形,若 , , , .则 的长为. 18. 在平面直角坐标系中,我们把横、纵坐标均为整数的点称为整点.若反比例函数 与二次函数 的图象在第一象限围成的封闭图形(不包括边界)内有且仅有2个整点,则实数 的取值范围为.
18. 在平面直角坐标系中,我们把横、纵坐标均为整数的点称为整点.若反比例函数 与二次函数 的图象在第一象限围成的封闭图形(不包括边界)内有且仅有2个整点,则实数 的取值范围为.三、解答题
-
19.(1)、计算: ;(2)、化简: .20. 解不等式组: ,并写出它的所有整数解.21. “生活垃圾分类”逐渐成为社会生活新风尚,某学校为了了解学生对“生活垃圾分类”的看法,随机调查了200名学生(每名学生必须选择且只能选择一类看法),调查结果分为“A.很有必要”“B.有必要”“C.无所谓”“D.没有必要”四类.并根据调查结果绘制了图1和图2两幅统计图(均不完整),请根据图中提供的信息,解答下列问题:
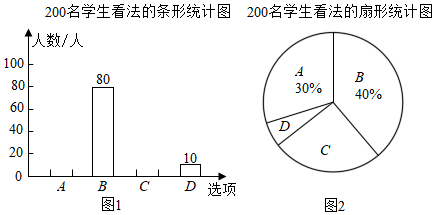 (1)、补全条形统计图;(2)、扇形统计图中“D.没有必要”所在扇形的圆心角度数为;(3)、该校共有2500名学生,根据调查结果估计该校对“生活垃圾分类”认为“A.很有必要”的学生人数.22. 随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷,现有“微信”、“支付宝”、“银行卡”三种支付方式.(1)、若随机选一种方式进行支付,则恰巧是“支付宝”的概率是;(2)、在一次购物中,小明和小亮都想从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付,求出两人恰好选择同一种支付方式的概率(用画树状图法或列表法求解).23. 高铁的开通为扬州市民的出行带来了方便.从扬州到某地,路程为 ,某趟高铁的平均速度比普通动车快50%,所需时间比普通动车少1小时,求该趟高铁的平均速度.24. 如图,菱形 的对角线 、 相交于点 , 是 的中点,点 、 在 边上, , .
(1)、补全条形统计图;(2)、扇形统计图中“D.没有必要”所在扇形的圆心角度数为;(3)、该校共有2500名学生,根据调查结果估计该校对“生活垃圾分类”认为“A.很有必要”的学生人数.22. 随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷,现有“微信”、“支付宝”、“银行卡”三种支付方式.(1)、若随机选一种方式进行支付,则恰巧是“支付宝”的概率是;(2)、在一次购物中,小明和小亮都想从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付,求出两人恰好选择同一种支付方式的概率(用画树状图法或列表法求解).23. 高铁的开通为扬州市民的出行带来了方便.从扬州到某地,路程为 ,某趟高铁的平均速度比普通动车快50%,所需时间比普通动车少1小时,求该趟高铁的平均速度.24. 如图,菱形 的对角线 、 相交于点 , 是 的中点,点 、 在 边上, , . (1)、求证:四边形 是矩形;(2)、若 , ,求 的长.25. 如图, 内接于⊙ , 是⊙ 的直径.直线 与⊙ 相切于点 ,在 上取一点 使得 .线段 , 的延长线交于点 .
(1)、求证:四边形 是矩形;(2)、若 , ,求 的长.25. 如图, 内接于⊙ , 是⊙ 的直径.直线 与⊙ 相切于点 ,在 上取一点 使得 .线段 , 的延长线交于点 .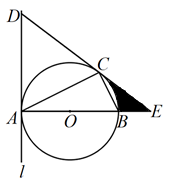 (1)、求证:直线 是⊙ 的切线;(2)、若 , ,求阴影部分的面积(结果保留 ).26. 近年来,随着盲盒经济的崛起,潮玩市场备受关注,盲盒里面通常装的是动漫、影视作品的周边,或者设计师单独设计出来的玩偶.某公司生产一种盲盒,在自动售卖机销售,已知这种盲盒的成本是每盒40元,物价局规定,这种盲盒的市场销售单价不得高于60元,不得低于45元.经市场调查发现,销售单价不高于50元时,每月销售量与销售单价成反比例函数关系;高于50元时,每月销售量与销售单价成一次函数关系,下表是部分市场调查数据:
(1)、求证:直线 是⊙ 的切线;(2)、若 , ,求阴影部分的面积(结果保留 ).26. 近年来,随着盲盒经济的崛起,潮玩市场备受关注,盲盒里面通常装的是动漫、影视作品的周边,或者设计师单独设计出来的玩偶.某公司生产一种盲盒,在自动售卖机销售,已知这种盲盒的成本是每盒40元,物价局规定,这种盲盒的市场销售单价不得高于60元,不得低于45元.经市场调查发现,销售单价不高于50元时,每月销售量与销售单价成反比例函数关系;高于50元时,每月销售量与销售单价成一次函数关系,下表是部分市场调查数据:销售单价/元
45
50
54
58
60
月销售量/盒
600
540
500
460
440
(1)、设月销售量为 盒,销售单价为 元,求 与 之间的函数关系式;(2)、当这种盲盒的销售单价为多少元时,月销售利润最大?月最大销售利润是多少元?27. 我们规定:三角形其中一边与该边上的高之比叫做这个三角形该边的 值.例如,如图1,在 中, , 上的高 ,则 边 的 值为 ,记作: . (1)、等腰直角三角形底边的 值= , 等边三角形任意一边的 值=;(2)、如图2,在 中, , ,求 .(3)、如图3,在矩形 中, , ,点 在矩形 内,且 .若以 为圆心,半径为1的圆与矩形 的对角线 有公共点,设点 到 的距离为 ,直接写出 的取值范围.28. 如图,在 中, , , ,射线 ,点 是边 上一动点,连接 ,过点 作 交射线 于点 ,连接 .
(1)、等腰直角三角形底边的 值= , 等边三角形任意一边的 值=;(2)、如图2,在 中, , ,求 .(3)、如图3,在矩形 中, , ,点 在矩形 内,且 .若以 为圆心,半径为1的圆与矩形 的对角线 有公共点,设点 到 的距离为 ,直接写出 的取值范围.28. 如图,在 中, , , ,射线 ,点 是边 上一动点,连接 ,过点 作 交射线 于点 ,连接 .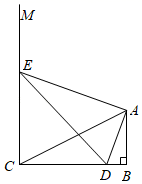 (1)、求证:点 、 、 、 在同一圆上;(2)、若 ,则 ;(3)、①当 面积的最大时,求 的长;
(1)、求证:点 、 、 、 在同一圆上;(2)、若 ,则 ;(3)、①当 面积的最大时,求 的长;②当点 从点 运动到点 时,直接写出 的外接圆圆心经过的路径长 ▲ .