江苏省盐城市盐都区2021年数学中考三模试卷
试卷更新日期:2021-10-21 类型:中考模拟
一、单选题
-
1. -9的绝对值是( )A、9 B、-9 C、 D、2. 下列图形中,是轴对称图形但不是中心对称图形的是( )A、圆 B、等腰三角形 C、平行四边形 D、菱形3. 过度包装既浪费资源又污染环境,据测算如果全国每年减少十分之一的包装纸用量那么能减少 吨二氧化碳的排放量,把 写成原数是( )A、 B、 C、 D、4. 下列运算正确的是( )A、a2+a2=a4 B、a3•a4=a12 C、(a3)4=a12 D、(ab)2=ab25. 如图所示物体的俯视图是( )

正面
A、 B、
B、 C、
C、 D、
D、 6. 如图,在菱形ABCD中,E是AB的中点,F点是AC的中点,连接EF.如果EF=4,那么菱形ABCD的周长为( )
6. 如图,在菱形ABCD中,E是AB的中点,F点是AC的中点,连接EF.如果EF=4,那么菱形ABCD的周长为( ) A、9 B、12 C、24 D、327. 如图,已知E(﹣4,2),F(﹣1,﹣1),以原点O为位似中心,按比例尺2:1把△EFO缩小,则E点对应点E′的坐标为( )
A、9 B、12 C、24 D、327. 如图,已知E(﹣4,2),F(﹣1,﹣1),以原点O为位似中心,按比例尺2:1把△EFO缩小,则E点对应点E′的坐标为( )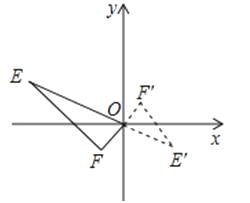 A、(2,1) B、( , ) C、(2,﹣1) D、(2,﹣)8. 若圆锥的底面半径为 ,侧面展开图的面积为 ,则圆锥的母线长为( )A、 B、 C、 D、
A、(2,1) B、( , ) C、(2,﹣1) D、(2,﹣)8. 若圆锥的底面半径为 ,侧面展开图的面积为 ,则圆锥的母线长为( )A、 B、 C、 D、二、填空题
-
9. 因式分解: =.10. 一个暗箱里装有5个黑球,3个白球,2个红球,每个球除颜色外都相同,从中任意摸出一个球,摸到红球的概率是.11. 如图,已知 ,则 的度数是.
 12. 甲乙两名同学在10次定点投篮训练中(每次训练投5个),每次训练成绩(投中的个数)如图所示,则甲乙两名同学投篮成绩比较稳定是;(填“甲”或“乙”)
12. 甲乙两名同学在10次定点投篮训练中(每次训练投5个),每次训练成绩(投中的个数)如图所示,则甲乙两名同学投篮成绩比较稳定是;(填“甲”或“乙”)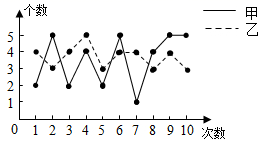 13. 如图,点 是反比例函数 图象上第二象限内的一点, 轴于点 ,若 的面积为6,则 的值为.
13. 如图,点 是反比例函数 图象上第二象限内的一点, 轴于点 ,若 的面积为6,则 的值为. 14. 如图,在⊙O的内接四边形ABCD中,∠A=70°,∠OBC=60°,则∠ODC=.
14. 如图,在⊙O的内接四边形ABCD中,∠A=70°,∠OBC=60°,则∠ODC=. 15. 某工厂计划m天生产2160个零件,若安排15名工人每人每天加工a个零件(a为整数)恰好完成.实际开工x天后,其中3人外出培训,剩下的工人每人每天多加工2个零件,不能按期完成这次任务,则a的值至少为.16. 如图,对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展平后再次折叠,使点A落在EF上的点A′处,得到折痕BM,BM与EF相交于点N.若直线BA′交直线CD于点O,BC=5,EN=1,则OD的长为.
15. 某工厂计划m天生产2160个零件,若安排15名工人每人每天加工a个零件(a为整数)恰好完成.实际开工x天后,其中3人外出培训,剩下的工人每人每天多加工2个零件,不能按期完成这次任务,则a的值至少为.16. 如图,对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展平后再次折叠,使点A落在EF上的点A′处,得到折痕BM,BM与EF相交于点N.若直线BA′交直线CD于点O,BC=5,EN=1,则OD的长为.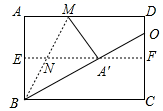
三、解答题
-
17. 计算:18. 解分式方程: .19. 先化简,再求值: ,其中x=﹣1.20. 4月18日上午7:30,2021盐城马拉松在盐城市盐南体育中心正式鸣枪开跑,共吸引了来自全国各地的约15000名选手同台竞技.本次马拉松共设三个项目:全程马拉松、半程马拉松、迷你马拉松.小乐和小观参加了该赛事的志愿者服务工作,组委会将志愿者随机分配到三个项目组中的一个.(1)、小乐被分配到半程马拉松项目组的概率为.(2)、用树状图或列表法求小乐和小观被分到同一个项目组的概率.21. 如图,在平行四边形 中, 平分 交 于点F.
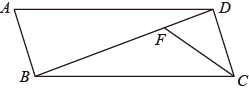 (1)、尺规作图:过点A作 平分 交 于点E;注意:不写作法,保留作图痕迹,并标明字母.(2)、求证: .22. 如图是某款手机支架摆放手机时的侧面示意图,现测得支撑板 , ,求手机底端E到底座 的距离.(精确到0.1,参考数据: , , , , , , )
(1)、尺规作图:过点A作 平分 交 于点E;注意:不写作法,保留作图痕迹,并标明字母.(2)、求证: .22. 如图是某款手机支架摆放手机时的侧面示意图,现测得支撑板 , ,求手机底端E到底座 的距离.(精确到0.1,参考数据: , , , , , , ) 23. 某校为了解九年级同学的体育考试准备情况,随机抽查该年级若干名学生进行体育模拟测试,根据测试成绩(单位:分)绘制成两幅不完整的统计图.请根据图中信息回答下面的问题:
23. 某校为了解九年级同学的体育考试准备情况,随机抽查该年级若干名学生进行体育模拟测试,根据测试成绩(单位:分)绘制成两幅不完整的统计图.请根据图中信息回答下面的问题: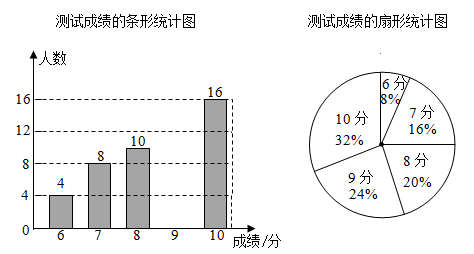 (1)、请补全条形统计图:(2)、所调查学生测试成绩的平均数为 , 中位数为 , 众数为;(3)、若该校九年级学生共有1500人,请估计该校九年级学生在体育模拟测试中不低于8分的学生约有多少人?24. 如图,AD是⊙O的直径,AB为⊙O的弦,OP⊥AD , OP与AB的延长线交于点P , 过点B的切线交OP于点C .
(1)、请补全条形统计图:(2)、所调查学生测试成绩的平均数为 , 中位数为 , 众数为;(3)、若该校九年级学生共有1500人,请估计该校九年级学生在体育模拟测试中不低于8分的学生约有多少人?24. 如图,AD是⊙O的直径,AB为⊙O的弦,OP⊥AD , OP与AB的延长线交于点P , 过点B的切线交OP于点C . (1)、求证:∠CBP=∠ADB;(2)、若OA=6,AB=4,求线段BP的长.25. 开学初期,天气炎热,水杯需求量大.双福育才中学门口某超市购进一批水杯,其中A种水杯进价为每个15元,售价为每个25元;B种水杯进价为每个12元,售价为每个20元(1)、该超市平均每天可售出60个A种水杯,后来经过市场调查发现,A种水杯单价每降低1元,则平均每天的销量可增加10个.为了尽量让学生得到更多的优惠,某天该超市将A种水杯售价调整为每个m元,结果当天销售A种水杯获利630元,求m的值.(2)、该超市准备花费不超过1600元的资金,购进A、B两种水杯共120个,其中B种水杯的数量不多于A种水杯数量的两倍.请为该超市设计获利最大的进货方案,并求出最大利润.26. 如图,直线y=﹣2x+4交x轴于点A,交y轴于点B,抛物线y=ax2+bx+c(a≠0)经过点A、E,点E的坐标是(5,3),抛物线交x轴于另一点C(6,0).
(1)、求证:∠CBP=∠ADB;(2)、若OA=6,AB=4,求线段BP的长.25. 开学初期,天气炎热,水杯需求量大.双福育才中学门口某超市购进一批水杯,其中A种水杯进价为每个15元,售价为每个25元;B种水杯进价为每个12元,售价为每个20元(1)、该超市平均每天可售出60个A种水杯,后来经过市场调查发现,A种水杯单价每降低1元,则平均每天的销量可增加10个.为了尽量让学生得到更多的优惠,某天该超市将A种水杯售价调整为每个m元,结果当天销售A种水杯获利630元,求m的值.(2)、该超市准备花费不超过1600元的资金,购进A、B两种水杯共120个,其中B种水杯的数量不多于A种水杯数量的两倍.请为该超市设计获利最大的进货方案,并求出最大利润.26. 如图,直线y=﹣2x+4交x轴于点A,交y轴于点B,抛物线y=ax2+bx+c(a≠0)经过点A、E,点E的坐标是(5,3),抛物线交x轴于另一点C(6,0). (1)、求抛物线的解析式.(2)、设抛物线的顶点为D,连接BD,AD,CD,动点P在BD上以每秒2个单位长度的速度由点B向点D运动,同时动点Q在线段CA上以每秒3个单位长度的速度由点C向点A运动,当其中一个点到达终点停止运动时,另一个点也随之停止运动,设运动时间为t秒,PQ交线段AD于点H.
(1)、求抛物线的解析式.(2)、设抛物线的顶点为D,连接BD,AD,CD,动点P在BD上以每秒2个单位长度的速度由点B向点D运动,同时动点Q在线段CA上以每秒3个单位长度的速度由点C向点A运动,当其中一个点到达终点停止运动时,另一个点也随之停止运动,设运动时间为t秒,PQ交线段AD于点H.①当∠DPH=∠CAD时,求t的值;
②过点H作HM⊥BD,垂足为点M,过点P作PN⊥BD交线段AB于点N.在点P、Q的运动过程中,是否存在以点P,N,H,M为顶点的四边形是矩形?若存在,求出t的值;若不存在,请说明理由.
27. (选一选,填一填)(1)、⊙O的直径为20,圆上两点M、N距离为16,⊙O上一动点A到直线MN距离的最大值为( )A、16 B、18 C、24 D、32(2)、等腰△ABC中,顶角∠ABC=45°,AM⊥BC,BN⊥AC,AM与BN交于点P,则 的值为.(3)、(画一画,算一算)
如图是某百姓休闲广场的部分平面示意图,直角梯形ABCD中,∠ABC=90°,∠ADC=120°,CD长60米,BC长80米, 点E在CD边上,且CE长40米.根据规划,要在直角梯形ABCD内确定一点F,AF长25米,同时建造展示区△FDE和休闲区△FBC.已知展示区造价每平方米200元,休闲区造价每平方米100元,建造好展示区和休闲区最少需要多少元?