江苏省盐城市盐都区、大丰区2021年数学中考二模试卷

试卷更新日期：2021-10-21 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列图形中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 计算a²·a⁴的结果是（）

A、a² B、a⁶ C、a⁸ D、a¹⁶

查看试题解析
3. 用科学记数法表示数0.031，其结果是（）

A、3.1×10² B、3.1×10^-2 C、0.31×10^-1 D、31×10³

查看试题解析
4. 如果不等式 $3 x - m \leq 0$ 有3个正整数解，那么 $m$ 的取值不可以是（）

A、9 B、10 C、11 D、12

查看试题解析
5. 已知线段a ， b ， c ，其中c是a和b的比例中项，a＝4，b＝9，则c=（）

A、4 B、6 C、9 D、36

查看试题解析
6. 如图，在直角△ $A B C$ 中， $∠ C A B = 90^{°}$ ， $∠ A B C = 70^{°}$ ， $A D$ 是 $∠ C A B$ 的平分线，交边 $B C$ 于点 $D$ ，过点 $C$ 作 $△ A C D$ 中 $A D$ 边上的高线 $C E$ ，则 $∠ E C D$ 的度数为（）

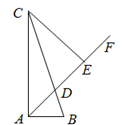A、35° B、30° C、25° D、20°

查看试题解析
7. 小丽准备通过爱心热线捐款，她只记得号码的前5位，后三位由 5，2，0 这三个数字组成，但具体顺序忘记了，她第一次就拨对电话的概率是（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{4}$ D、 $\frac{1}{6}$

查看试题解析
8. 如图，在扇形OAB中，OC⊥AB于点D ， AB＝8，将△ODB绕点O逆时针旋转60°，则线段DB扫过的图形面积为（）

A、 $\frac{4 π}{3}$ B、 $2 π$ C、 $\frac{8 π}{3}$ D、 $\frac{10 π}{3}$

查看试题解析

二、填空题

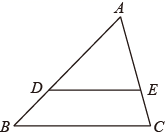
9. 计算（＋2）＋（－3）其结果是．

查看试题解析
10. 分解因式：m²﹣2m= ．

查看试题解析
11. 甲、乙两支仪仗队的队员人数相同，平均身高相同，身高的方差分别为S²_甲=0.9，S²_乙=1.1，则甲、乙两支仪仗队的队员身高更整齐的是（填“甲”或“乙”）．

查看试题解析
12. 方程组 ${\begin{array}{l} x - y = 1 \\ 2 x + y = 5 \end{array}$ 的解是．

查看试题解析
13. 将一个内部直径为 $20 cm$ 、高为 $10 cm$ 的圆柱形水桶内装满水，然后倒入一个长方形鱼缸中，水只占鱼缸容积的一半，则鱼缸容积为 ${cm}^{3}$ ．

查看试题解析
14. 如图， $D$ 、 $E$ 分别是 $△ A B C$ 边 $A B$ 、 $A C$ 上的点， $D E / / B C$ ， $A D = 5$ ， $B D = 3$ ， $B C = 4$ ，则 $D E$ 长为．

查看试题解析
15. 若反比例函数 $y = \frac{k}{x}$ 与一次函数 $y = x + 2$ 的图象只有一个交点，则 $k$ = ．

查看试题解析
16. 如图，在矩形ABCD中，AB＝13，BC＝17，点E是线段AD上一个动点，把△BAE沿BE向矩形内部折叠，当点A的对应点A₁恰好落在∠BCD的平分线上时，AE的长为．

查看试题解析

三、解答题

17. 计算： $\sqrt{3} (\sqrt{3} + 1) + \frac{1}{2 + \sqrt{3}}$

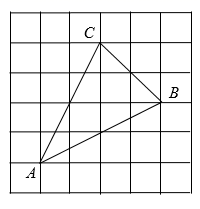
查看试题解析
18. 先化简，再求值：(x+1)(x-1)+x(3-x)，其中x=2．

查看试题解析
19. 如图，网格小正方形的边长都为 $1$ ，在 $Δ A B C$ 中，试利用格点分别画出：边AC上的中线BM、边AB上的高CH ，并判断 $Δ A B C$ 的形状．

查看试题解析
20.

(1)、画出反比例函数 $y = - \frac{4}{x}$ 的大致图象，结合图象回答：

(2)、当 $x = 2$ 时， $y$ 的值；

(3)、当 $1 < x \leq 4$ 时， $y$ 的取值范围；

(4)、当 $- 1 \leq y < 4$ 且 $y \neq 0$ 时， $x$ 的取值范围．

查看试题解析

21. 为了让学生了解环保知识，增强环保意识，某校组织七、八年级各200名学生对相关知识进行学习并组织定时测试．现分别在七、八两个年级中各随机抽取了10名学生，统计这部分学生的测试成绩，相关数据整理如下：

七年级：74，86，74，93，81，71，80，87，77，97；

八年级：87，74，94，86，82，76，77，82，78，84．

分别计算两组数据的平均数、中位数、众数、方差，填入下表（部分结果已填入）：

年级	平均数	中位数	众数	方差
七年级	82	①	74	66.6
八年级	②	82	③	④

（平均数： $\bar{x} = \frac{1}{n} (x_{1} + x_{2} + \cdot \cdot \cdot + x_{n})$ ，方差： $s^{2} = \frac{1}{n} [{(x_{1} - \bar{x})}^{2} + {(x_{2} - \bar{x})}^{2} + \cdot \cdot \cdot + {(x_{n} - \bar{x})}^{2}]$ ）

查看试题解析

22. 由中宣部建设的“学习强国”学习平台正式上线，这是推动习近平新时代中国特色社会主义思想，推进马克思主义学习型政党和学习型社会建设的创新举措．某基层党组织对党员的某天学习成绩进行了整理，分成5个小组（x表示成绩，单位：分，且20≤x＜70），根据学习积分绘制出部分频数分布表，其中第2、第5两组测试成绩人数之比为4：1，请结合下表中相关数据回答问题：

学习积分频数分布表
组别	成绩x分	频数	频率
第1组	20≤x＜30	5
第2组	30≤x＜40
第3组	40≤x＜50	15	0.30
第4组	50≤x＜60	10
第5组	60≤x＜70	a	b

(1)、填空：a＝， b＝；

(2)、已知该基层党组织中甲、乙两位党员的学习积分分别为63分、67分，现在从这组中随机选取2人介绍经验，请用列表、画树状图等方法，求出甲、乙两人同时被选中的概率．

查看试题解析

23. 如图，在正方形ABCD中，点M是BC边上的任一点，连接AM并将线段AM绕点M顺时针旋转90°得到线段MN ，在CD边上取点P使CP＝BM ，连接NP、BP ．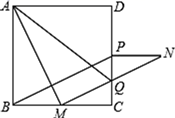

(1)、求证：BP＝MN；

(2)、线段MN与CD交于点Q ，连接AQ ，若△MCQ∽△AMQ ，试证明BM=MC ．

查看试题解析
24. 某商店经销一种成本为每千克80元的水果，据市场分析，若按每千克100元销售，一个月能售出500千克．若销售价每涨5元，则月销售量减少20千克．针对这种水果的销售情况请解答以下问题：

(1)、当销售单价为每千克110元时，计算月销售量和月销售利润；

(2)、商店想在月销售成本不超过20000元的情况下，使月销售利润达到12000元，销售单价应定为多少元？

查看试题解析
25. 吾悦广场准备在地下停车场北侧建设一个供小型货车进出的专用入口，如图，入口设计示意图中，一楼到地下停车场地面的垂直高度CD＝300 cm ，一楼到地平线的距离BC＝90 cm ．经调查，送货的小型货车高度都低于268 cm ，为了保证货物安全，入口处货车顶部要留有不少于20 cm的安全距离．为尽量减少施工量，应在地面上距点B多远的A处开始斜坡AD的施工？

查看试题解析
26. 如图，将一副斜边相等的直角三角板按斜边重合摆放在同一平面内，其中∠DAB＝45°，∠CAB＝30°，点O为斜边AB的中点，连接CD交AB于点E ．设AB＝1．

(1)、求证：A、B、C、D四个点在以点O为圆心的同一个圆上；

(2)、分别求△ABC和△ABD的面积；

(3)、过点D作DF∥BC交AB于点F ，求OE︰OF的比值．

查看试题解析
27. 如图坐标系中，矩形ABCD的边BC在 y轴上，B（0，8），BC＝10，CD＝5，将矩形ABCD绕点B逆时针旋转使点C落在x轴上．现已知抛物线y＝ax²＋bx＋c（a≠0）过点D、C′和原点O ．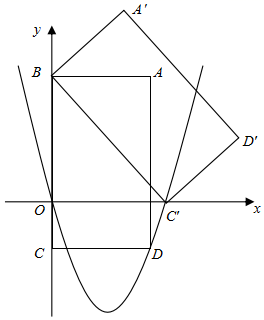

(1)、求抛物线的解析式；

(2)、将矩形A′BC′D′沿直线BC′翻折，点A′的对应点为M ，请判断点M是否在所给抛物线上，并简述理由；

(3)、在抛物线上是否存在一点P ，使∠POC′＝2∠CBD ，若存在，求出点P的坐标，若不存在，请说明理由；

查看试题解析