江苏省盐城市射阳县2021年数学中考三模试卷
试卷更新日期:2021-10-21 类型:中考模拟
一、单选题
-
1. 图中为某几何体的分别从上面、前面、左边看到的三个图形,该几何体是( )
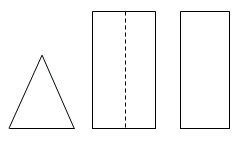 A、圆锥 B、圆柱 C、三棱柱 D、三棱锥2. 我国是最早认识负数,并进行相关运算的国家在古代数学名著《九章算术》里,就记载了利用算筹实施“正负术”的方法,图1表示的是计算 的过程按照这种方法,图2表示的过程应是在计算( )
A、圆锥 B、圆柱 C、三棱柱 D、三棱锥2. 我国是最早认识负数,并进行相关运算的国家在古代数学名著《九章算术》里,就记载了利用算筹实施“正负术”的方法,图1表示的是计算 的过程按照这种方法,图2表示的过程应是在计算( )
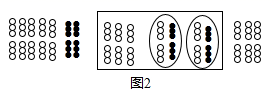 A、 B、 C、5+2 D、3. 下列计算正确的是( )A、 B、 C、 D、4. AF是 的平分线, 若 则 的度数为( )
A、 B、 C、5+2 D、3. 下列计算正确的是( )A、 B、 C、 D、4. AF是 的平分线, 若 则 的度数为( ) A、17.5° B、35° C、55° D、70°5. 已知线段 , , ,求作: ,使 , , .下面的作图顺序正确的是( )
A、17.5° B、35° C、55° D、70°5. 已知线段 , , ,求作: ,使 , , .下面的作图顺序正确的是( )①以点 为圆心,以 为半径画弧,以点 为圆心,以 为半径画弧,两弧交于 点;②作线段 等于 ;③连接 , ,则 就是所求作图形.
A、①②③ B、③②① C、②①③ D、②③①6. 永宁县某中学在预防“新冠肺炎”期间,要求学生每日测量体温,九(5)班一名同学连续一周体温情况如下表所示:则该名同学这一周体温数据的众数和中位数分别是( )日期
星期一
星期二
星期三
星期四
星期五
星期六
星期天
体温(℃)
36.2
36.2
36.5
36.3
36.2
36.4
36.3
A、36.3和36.2 B、36.2和36.3 C、36.2和36.2 D、36.2和36.17. 如图,点A,B是 上的定点,点P为优弧 上的动点(不与点A,B重合),在点P运动的过程中,以下结论正确的是( ) A、 的大小改变 B、点P到弦 所在直线的距离存在最大值 C、线段 与 的长度之和不变 D、图中阴影部分的面积不变8. 使用家用燃气灶烧开同一壶水所需的燃气量 (单位: )与旋钮的旋转角度 (单位:度)( )近似满足函数关系y=ax2+bx+c(a≠0).如图记录了某种家用燃气灶烧开同一壶水的旋钮角度 与燃气量 的三组数据,根据上述函数模型和数据,可推断出此燃气灶烧开一壶水最节省燃气的旋钮角度约为( )
A、 的大小改变 B、点P到弦 所在直线的距离存在最大值 C、线段 与 的长度之和不变 D、图中阴影部分的面积不变8. 使用家用燃气灶烧开同一壶水所需的燃气量 (单位: )与旋钮的旋转角度 (单位:度)( )近似满足函数关系y=ax2+bx+c(a≠0).如图记录了某种家用燃气灶烧开同一壶水的旋钮角度 与燃气量 的三组数据,根据上述函数模型和数据,可推断出此燃气灶烧开一壶水最节省燃气的旋钮角度约为( )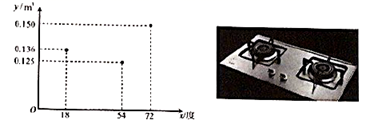 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
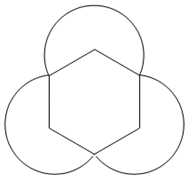
9. 第七次全国人口普查结果公布,全国人口共14.1178亿.请把14.1178亿记成科学记数法.10. 分解因式:m2n﹣4n=.11. 方程x2-7x+10=0的两个根是等腰三角形的两边长,则该等腰三角形的周长是12. 在平面直角坐标系中,已知点 , ,以原点 为位似中心,把 按相似比 缩小,则点 的对应点 的坐标是.13. 某同学以一个边长为1的正六边形的三个顶点为圆心,边长为半径,向外画了三段圆弧,设计了如图所示的图案.则图案外围轮廓的周长为.
 14. 目前,步行已成为人们最喜爱的健身方法之一,通过手机可以计算行走的步数与相应的能量消耗.对比手机数据发现:小琼步行13500步与小刚步行9000步消耗的能量相同.若每消耗1千卡能量小琼行走的步数比小刚多15步.设小刚每消耗1千卡能量需要行走 步,则根据题意可列方程为.15. 如图, 中, 厘米, 厘米,点 为 的中点,如果点 在线段 上以 厘米/秒的速度由 点向 点运动,同时,点 在线段 上由 点向 点运动.若点 的运动速度为 厘米/秒,则当 与 全等时, 的值为.
14. 目前,步行已成为人们最喜爱的健身方法之一,通过手机可以计算行走的步数与相应的能量消耗.对比手机数据发现:小琼步行13500步与小刚步行9000步消耗的能量相同.若每消耗1千卡能量小琼行走的步数比小刚多15步.设小刚每消耗1千卡能量需要行走 步,则根据题意可列方程为.15. 如图, 中, 厘米, 厘米,点 为 的中点,如果点 在线段 上以 厘米/秒的速度由 点向 点运动,同时,点 在线段 上由 点向 点运动.若点 的运动速度为 厘米/秒,则当 与 全等时, 的值为.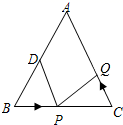 16. 如图,直线 与x轴交于点B,与双曲线 (x>0)交于点A,过点B作x轴的垂线,与双曲线 交于点C.且AB=AC,则k的值为.
16. 如图,直线 与x轴交于点B,与双曲线 (x>0)交于点A,过点B作x轴的垂线,与双曲线 交于点C.且AB=AC,则k的值为.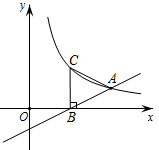
三、解答题
-
17.(1)、计算: ;(2)、化简: .18. 为纪念并缅怀当今神农袁隆平为解决人类温饱问题所建立的丰功伟绩,扎实推进“光盘行动”,某校八年级举办“缅怀伟人,拒绝浪费,从我做起”的学生演讲比赛,八(1)班准备从小怡、小宏、小童、小灿4名同学之中选择两名参加比赛,选择方案如下:制作4张完全相同的卡片,正面分别写上这4名同学的姓名,将卡片反面朝上洗匀,张老师从4张卡片中随机抽取1张卡片不放回,再抽取一张,卡片正面是谁的名字,谁就代表班级参加比赛.(注:可以用 、 、 、 分别表示小怡、小宏、小童、小灿的名字)(1)、用树状图或列表法列出所有等可能结果;(2)、求小怡和小宏同时被选中的概率.19. 小李家准备购买一台台式电脑,小李将收集到的该地区 , , 三种品牌电脑销售情况的有关数据统计如下:

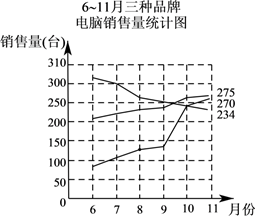
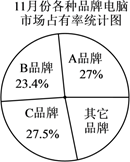
根据上述三个统计图,请解答:
(1)、直接写出6至11月三种品牌电脑销售总量最多的电脑品牌,以及11月份A品牌电脑的销售量;(2)、11月份,其它品牌的电脑销售总量是多少台?(3)、你建议小李购买哪种品牌的电脑?请写出你的理由(写出一条理由即可).20. 已知 , , ,求代数式 的值.21. 港珠澳大桥,从2009年开工建造,于2018年10月24日正式通车.其全长55公里,连接港珠澳三地,集桥、岛、隧于一体,是世界上最长的跨海大桥.如图是港珠澳大桥的海豚塔部分效果图,为了测得海豚塔斜拉索顶端A距离海平面的高度,先测出斜拉索底端C到桥塔的距离(CD的长)约为100米,又在C点测得A点的仰角为30°,测得B点的俯角为20°,求斜拉索顶端A点到海平面B点的距离(AB的长).(已知 ≈1.73,tan20°≈0.36,结果精确到0.1) 22. 如图,一次函数 的图象与反比例函数 的图象相交于 , 两点直线 分别交 轴、 轴于 、 两点.
22. 如图,一次函数 的图象与反比例函数 的图象相交于 , 两点直线 分别交 轴、 轴于 、 两点.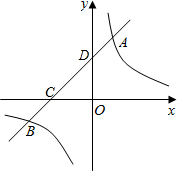 (1)、直接写出不等式 的解集;(2)、求 的值;(3)、求 点的坐标.23. 如图,正方形 的对角线 、 相交于点 , 、 分别在 、 上, .写出 与 的关系,并说明理由.
(1)、直接写出不等式 的解集;(2)、求 的值;(3)、求 点的坐标.23. 如图,正方形 的对角线 、 相交于点 , 、 分别在 、 上, .写出 与 的关系,并说明理由.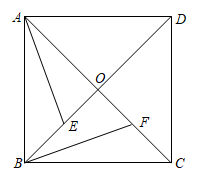 24. 如图, 是 的直径, 交 于点 , 是弧 的中点, 与 交于点 , .
24. 如图, 是 的直径, 交 于点 , 是弧 的中点, 与 交于点 , .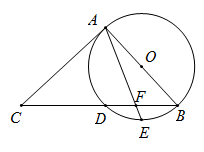 (1)、求证: 是 的切线;(2)、若 , ,求 的长.25. 某市为创建“全国文明城市”,计划购买甲、乙两种树苗绿化城区,购买50棵甲种树苗和20棵乙种树苗需要5000元,购买30棵甲种树苗和10棵乙种树苗需要2800元.(1)、求购买的甲、乙两种树苗每棵各需要多少元.(2)、经市绿化部门研究,决定用不超过42000元的费用购买甲、乙两种树苗共500棵,其中乙种树苗的数量不少于甲种树苗数量的 ,求甲种树苗数量的取值范围.(3)、在(2)的条件下,如何购买树苗才能使总费用最低?26. (阅读理解)设点 在矩形 内部,当点 到矩形的一条边的两个端点距离相等时,称点 为该边的“和谐点”.例如:如图1,矩形 中,若 ,则称 为边 的“和谐点”.
(1)、求证: 是 的切线;(2)、若 , ,求 的长.25. 某市为创建“全国文明城市”,计划购买甲、乙两种树苗绿化城区,购买50棵甲种树苗和20棵乙种树苗需要5000元,购买30棵甲种树苗和10棵乙种树苗需要2800元.(1)、求购买的甲、乙两种树苗每棵各需要多少元.(2)、经市绿化部门研究,决定用不超过42000元的费用购买甲、乙两种树苗共500棵,其中乙种树苗的数量不少于甲种树苗数量的 ,求甲种树苗数量的取值范围.(3)、在(2)的条件下,如何购买树苗才能使总费用最低?26. (阅读理解)设点 在矩形 内部,当点 到矩形的一条边的两个端点距离相等时,称点 为该边的“和谐点”.例如:如图1,矩形 中,若 ,则称 为边 的“和谐点”.(解题运用)已知,点 在矩形 内部,且 , .
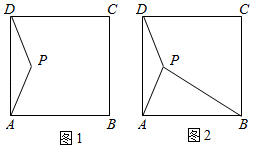 (1)、设 是边 的“和谐点”,则 ▲ 边 的“和谐点”(填“是”或“不是”);连接 , ,求 的值.(2)、若 是边 的“和谐点”,连接 , ,当 时,求 的值;(3)、如图2,若 是边 的“和谐点”,连接 ; , ,求 的最大值.27. 如图,抛物线 经过 、 、 三点,对称轴与抛物线相交于点 ,与直线 相交于点 ,连接 , .
(1)、设 是边 的“和谐点”,则 ▲ 边 的“和谐点”(填“是”或“不是”);连接 , ,求 的值.(2)、若 是边 的“和谐点”,连接 , ,当 时,求 的值;(3)、如图2,若 是边 的“和谐点”,连接 ; , ,求 的最大值.27. 如图,抛物线 经过 、 、 三点,对称轴与抛物线相交于点 ,与直线 相交于点 ,连接 , .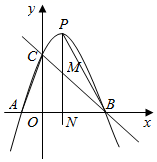 (1)、求该抛物线的解析式;(2)、设对称轴与 轴交于点 ,在对称轴上是否存在点 ,使以 、 、 为顶点的三角形与 相似?如果存在,请求出点 的坐标;如果不存在,请说明理由;(3)、抛物线上是否存在一点 ,使 与 的面积相等,若存在,求点 的坐标;若不存在,请说明理由;(4)、点 是 轴上的动点,连接 ,求 的最小值.
(1)、求该抛物线的解析式;(2)、设对称轴与 轴交于点 ,在对称轴上是否存在点 ,使以 、 、 为顶点的三角形与 相似?如果存在,请求出点 的坐标;如果不存在,请说明理由;(3)、抛物线上是否存在一点 ,使 与 的面积相等,若存在,求点 的坐标;若不存在,请说明理由;(4)、点 是 轴上的动点,连接 ,求 的最小值.