江苏省盐城市滨海县2021年九年级第一次调研检测数学试卷
试卷更新日期:2021-10-21 类型:中考模拟
一、单选题
-
1. 下列温度比-5℃低的是( )A、-3℃ B、-8℃ C、0℃ D、3℃
-
2. 一实验室检测A、B、C、D四个零件的质量(单位∶克),超过标准质量的克数记为正数,不足标准质量的克数记为负数,结果如图所示,其中最接近标准质量的零件是( )A、
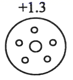 B、
B、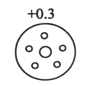 C、
C、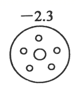 D、
D、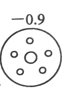
-
3. 2020年6月23日,中国第55颗北斗导航卫星成功发射,顺利完成全球组网.其中支持北斗三号新信号的22纳米工艺射频基带一体化导航定位芯片,已实现规模化应用.22纳米=0.000000022米,将0.000000022用科学记数法表示为( )A、 B、 C、 D、
-
4. 如图所示的几何体的俯视图是( )
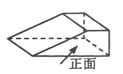 A、
A、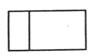 B、
B、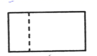 C、
C、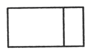 D、
D、
-
5. 要调查下列问题,适合采用全面调查(普查)的是( )A、中央电视台《开学第一课》的收视率 B、即将发射的气象卫星的零部件质量 C、某城市居民6月份人均网上购物的次数 D、某品牌新能源汽车的最大续航里程
-
6. 如图,AB和CD相交于点O,则下列结论正确的是( )
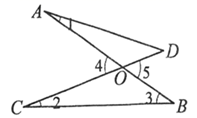 A、∠1=∠3 B、∠5=∠1+∠3 C、∠4=∠5 D、∠5<∠2
A、∠1=∠3 B、∠5=∠1+∠3 C、∠4=∠5 D、∠5<∠2 -
7. 如图,数轴上两点 所对应的实数分别为 ,则 的结果可能是( )
 A、-1 B、1 C、2 D、3
A、-1 B、1 C、2 D、3 -
8. 如图,AB为⊙O的切线,点A为切点,OB交⊙O于点C,点D在⊙O上,连接AD、CD、OA,若∠ADC=30°,则∠ABO的度数为( )
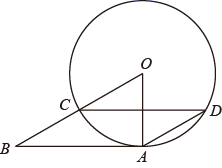 A、25° B、20° C、30° D、35°
A、25° B、20° C、30° D、35°
二、填空题
-
9. 分解因式∶4m2-n2=
-
10. 若分式 的值等于1,则x=.
-
11. 《易经》是中华民族聪明智慧的结晶.如图是《易经》中的一种卦图,每一卦由三根线组成(线形为“—”或“﹣﹣”),如正南方向的卦为“☴”.从图中任选一卦,这一卦中恰有2根“—”和1根“﹣﹣”的概率是.

-
12. 设M=x+y,N=x-y,P=xy.若M=2,N=4,则P=.
-
13. 《九章算术》是我国古代一部著名的算书,它的出现标志着中国古代数学形成了完整的体系其中卷八方程[七]中记载:“今有牛五、羊二,直金十两.牛二、羊五,直金八两.牛、羊各直金几何?”题目大意是:5头牛、2只羊共值金10两.2头牛、5只羊共值金8两.每头牛、每只羊各值金多少两?设1头牛值金 两,1只羊值金 两,则可列方程组为.
-
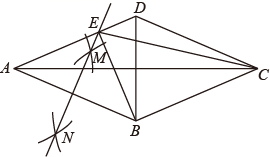
14. 如图,在菱形ABCD中,∠DAB=40°,分别以点A、B为圆心,大于 AB的长为半径作弧相交于两点,过此两点的直线交AD边于点E(作图痕迹如图所示),连接BE、BD.则∠EBD的度数为.
-
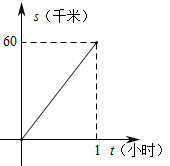
15. 某日上午,甲、乙两车先后从A地出发沿同一条公路匀速前往B地,甲车8点出发,如图是其行驶路程s(千米)随行驶时间t(小时)变化的图象.乙车9点出发,若要在当天12点至13点之间(含12点和13点)追上甲车,则乙车的速度v(单位∶千米/小时)的范围是.
-
16. 如图,矩形ABCD中,E是AB上一点,连接DE,将△ADE沿DE翻折,恰好使点A落在BC边的中点F处,在DF上取点O,以O为圆心,OF长为半径作半圆与CD相切于点G.若AD=6,则图中阴影部分的面积为

三、解答题
-
17. 计算∶(1- )0+∣-3∣+
-
18. 解不等式组:
-
19. 先化简,再求值∶ ,其中 .
-
20. 如图,在△ABC中,∠B=∠C,过BC的中点D作DE⊥AB,DF⊥AC,垂足分别为点E、F.
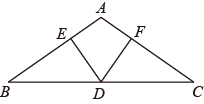 (1)、求证∶DE=DF;(2)、若∠BDE=55°,求∠BAC的度数.
(1)、求证∶DE=DF;(2)、若∠BDE=55°,求∠BAC的度数. -
21. 现有4张正面分别写有数字1、2、3、4的卡片,将4张卡片的背面朝上,洗匀.(1)、若从中任意抽取1张,抽的卡片上的数字恰好为3的概率是;(2)、若先从中任意抽取1张(不放回),再从余下的3张中任意抽取1张,求抽得的2张卡片上的数字之和为3的倍数的概率.(请用“画树状图”或“列表”等方法写出分析过程)
-
22. 如图,一次函数 的图象与反比例函数 ( 为常数且 )的图象相交于 ,B两点.
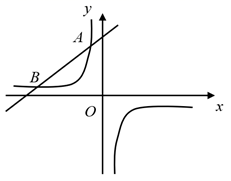 (1)、求反比例函数的表达式;(2)、将一次函数 的图象沿 轴向下平移 个单位 ,使平移后的图象与反比例函数 的图象有且只有一个交点,求b的值.
(1)、求反比例函数的表达式;(2)、将一次函数 的图象沿 轴向下平移 个单位 ,使平移后的图象与反比例函数 的图象有且只有一个交点,求b的值. -
23. 小亮家准备购买一台电视机,小亮将收集到的某地区A、B、C三种品牌电视机销售情况的有关数据统计如下∶
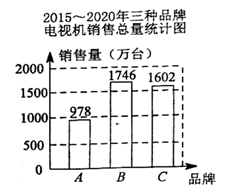
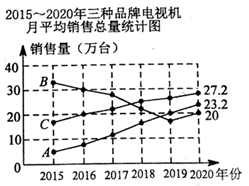
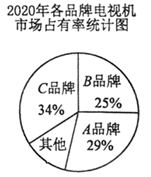
根据上述三个统计图,请解答∶
(1)、2015~2020年三种品牌电视机销售总量最多的是品牌,月平均销售量最稳定的是品牌.(2)、2020年其他品牌的电视机月平均销售总量是多少万台?(3)、货比三家后,你建议小亮家购买哪种品牌的电视机?说说你的理由. -
24. 如图,△ABD中,∠ABD=∠ADB.
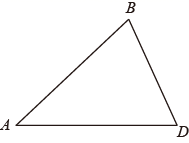 (1)、作点A关于BD的对称点C;(要求∶尺规作图,不写作法,保留作图痕迹)(2)、在(1)所作的图中,连接BC、DC,连接AC,交BD于点O.
(1)、作点A关于BD的对称点C;(要求∶尺规作图,不写作法,保留作图痕迹)(2)、在(1)所作的图中,连接BC、DC,连接AC,交BD于点O.①求证∶四边形ABCD是菱形;
②取BC的中点E,连接OE,若OE= ,BD=14,求点E到AD的距离
-
25. 如图,AB是⊙O的直径,C是⊙O上一点,OD⊥AC于点D,过点C作⊙O的切线,交OD的延长线于点M,OM交⊙O于点N,连结AM.
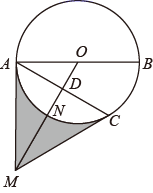 (1)、求证:AM是⊙O的切线;(2)、若DN=4,AC=8 ,求线段MN的长;(3)、在(2)的条件下,求阴影部分的面积.
(1)、求证:AM是⊙O的切线;(2)、若DN=4,AC=8 ,求线段MN的长;(3)、在(2)的条件下,求阴影部分的面积. -
26. 如图①,在△ABC中,∠A=90°,AB=AC= ,点D、E分别在边AB、AC上,AD=AE= ,连接DE,把△ADE绕点A顺时针方向旋转α(0°<α<360°).
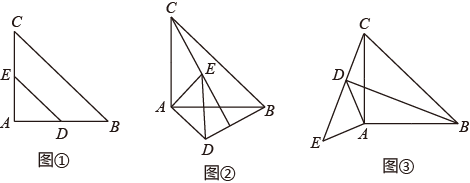 (1)、如图②,当0°<α<180°时,判断线段CE和BD的数量关系,并说明理由;(2)、如图③,若180°<α<360°,当C、D、E三点在同一直线时,BD与CE具有怎样的位置关系,请说明理由,并求出此时线段BE的长;(3)、在旋转过程中,求△BCD的面积的最大值,并写出此时的旋转角α的度数.
(1)、如图②,当0°<α<180°时,判断线段CE和BD的数量关系,并说明理由;(2)、如图③,若180°<α<360°,当C、D、E三点在同一直线时,BD与CE具有怎样的位置关系,请说明理由,并求出此时线段BE的长;(3)、在旋转过程中,求△BCD的面积的最大值,并写出此时的旋转角α的度数. -
27. 如图1,一次函数y=-x-3的图象与x轴交于点A,与y轴交于点C,过A、C两点的抛物线y=ax²+bx+c与x轴交于另一点B(1,0)
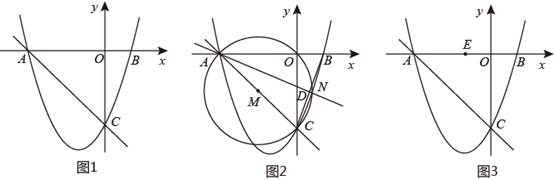 (1)、求抛物线的解析式;(2)、如图2,连接BC,若点D为BC的中点.
(1)、求抛物线的解析式;(2)、如图2,连接BC,若点D为BC的中点.①求直线AD的表达式;
②以AC为直径作⊙M交直线AD于点N,求点N的坐标;
(3)、如图3,若点E为AB的中点,点F为抛物线上一点,直线EF与AC所夹锐角为α,且tanα= ,求点F的坐标(直接写出坐标).
