江苏省苏州市吴中区、吴江区、相城区2021年数学中考二模试卷

试卷更新日期：2021-10-21 类型：中考模拟

进入出卷网下载

一、单选题

1. 实数-2的绝对值是（）

A、-2 B、2 C、 $\frac{1}{2}$ D、 $- \frac{1}{2}$

查看试题解析
2. 北斗三号全球卫星导航系统正式开通运行，北斗导航系统创新融合了导航与通信能力，亚太地区通信能力可以达到每次14000比特，能传输文字，还可以传输语音和图片.其中，数字14000用科学记数法可表示为（）

A、14×10³ B、1.4×10³ C、14×10⁴ D、1.4×10⁴

查看试题解析
3. 下列运算结果正确的是（）

A、（a³）³＝a⁹ B、（a﹣b）³＝a³﹣b³ C、a³+a³＝a⁶ D、a³÷a³＝a

查看试题解析
4. 如图，直线a、b被直线c、d所截，下列条件能判定直线a∥b的是（）

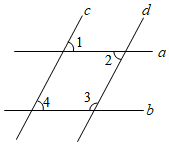A、∠1＝∠2 B、∠1＝∠4 C、∠2＝∠4 D、∠3+∠4＝180°

查看试题解析
5. 已知反比例函数y＝ $\frac{k + 1}{x}$ （k为常数）的图象经过第一、三象限，则k的取值范围是（）

A、k＞1 B、k＜1 C、k＞﹣1 D、k＜﹣1

查看试题解析
6. 一组数据：1、2、2、3，若添加一个数据2，则发生变化的统计量是（）

A、平均数 B、中位数 C、众数 D、方差

查看试题解析
7. 某几何体的主视图和俯视图及相关数据（单位：cm）如图所示，则该几何体的侧面积是（）

A、60πcm² B、65πcm² C、90πcm² D、120πcm²

查看试题解析
8. 如图，菱形ABCD的两边与⊙O分别相切于点A、C，点D在⊙O上，则∠B的度数是（）

A、45° B、50° C、60° D、65°

查看试题解析
9. 如图，在△ABC中，∠C＝2∠B，分别以点A、B为圆心，大于 $\frac{1}{2}$ AB的长为半径画弧，两弧交于点M、N，作直线MN，交BC边于点D，连接AD，若AD＝5，CD＝6，则AB的长是（）

A、5 $\sqrt{3}$ B、8 C、4 $\sqrt{5}$ D、10

查看试题解析
10. 用一段长为20m的篱笆围成一个矩形菜园，设菜园的对角线长为xm，面积为ym² ，则y与x的函数图象大致是（）

A、 B、 C、 D、

查看试题解析

二、填空题

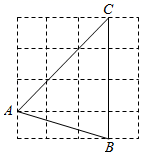
11. 使分式 $\frac{1}{x - 3}$ 有意义的x的取值范围是．

查看试题解析
12. 近年来，我国城乡居民的收入有了大幅提高，为了了解我国城乡居民收入10年来的变化趋势，适合采用的统计图是 .（填“扇形统计图”或“折线统计图”）

查看试题解析
13. 分解因式：（a+b）²﹣4ab= ．

查看试题解析
14. 若线段DE是等边△ABC的中位线，且DE＝2，则△ABC的周长为 .

查看试题解析
15. 沧浪亭、狮子林、拙政园、留园是苏州四大名园，分别代表着宋、元、明、清四个朝代的艺术风格，小明想选择其中两个名园游玩，则选到拙政园和留园的概率是.

查看试题解析
16. 如图，△ABC的顶点在正方形网格的格点上，则sinA的值为.

查看试题解析
17. 如图，在平面直角坐标系中，正方形ABCD的顶点A、C分别在x轴和y轴的正半轴上，点A（1，0），点C（0，5），反比例函数的图象经过点B，则k的值为 .

查看试题解析

三、解答题

18. 如图，在Rt△ABC中，∠A＝90°，AB＝4，AC＝3，M、N、P分别是边AB、AC、BC上的动点，连接PM、PN和MN，则PM+PN+MN的最小值是 .

查看试题解析
19. 计算：（﹣2）²﹣ $\sqrt{4}$ +（3﹣π）⁰.

查看试题解析
20. 解不等式组： ${\begin{array}{l} 2 x + 2 \geq x \\ 1 - \frac{x + 1}{2} > \frac{x - 1}{3} \end{array}$ .

查看试题解析
21. 先化简，再求值： $(1 - \frac{1}{x + 2}) \div \frac{x^{2} - 1}{x + 2}$ ，其中 $x = \sqrt{2} + 1$ ．

查看试题解析

22. 某中学为提升该校九年级学生假期复习效率，组织了本校教师开展线上教学，为了解学生线上教学的学习效果，决定随机抽取九年级部分学生进行质量测评，以下是根据测试的数学成绩绘制的统计表和频数分布直方图：

	成绩x/分	频数	频率
第1段	x＜60	2	0.04
第2段	60≤x＜70	6	0.12
第3段	70≤x＜80	9	b
第4段	80≤x＜90	a	0.36
第5段	90≤x≤100	15	0.30

请根据所给信息，解答下列问题：

(1)、a＝， b＝；

(2)、此次抽样的样本容量是 ▲ ，并补全频数分布直方图；

(3)、在抽取的样本中，某同学的数学成绩为75分，则数学成绩高于75分的至少有人；

(4)、已知该年级有600名学生参加测试，请估计该年级数学成绩为优秀（90分及以上）的人数.

查看试题解析

23. 如图，在△ABC中，点D、E、F分别在AB、BC、AC边上，DE∥AC，EF∥AB.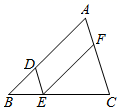

(1)、求证：△BDE∽△EFC；

(2)、若 $\frac{A F}{F C} = \frac{1}{2}$ ，且S_△DBE＝2，求△ABC的面积.

查看试题解析
24. 苏州轨道交通1号线是苏州市第一条建成运营的地铁线路，于2012年4月28日开通运营，现有甲列车从1号线站台A开往站台B，途经站台C，乙列车从站台C开往站台A，甲、乙两列车的平均速度相同，两列车距离站台C的路程y（km）与行驶时间t（min）的函数图象如图所示，结合图象信息，解答下列问题：

(1)、甲、乙两列车的平均速度是km/min，图中m＝；

(2)、直接写出甲列车出发几分钟后，两列车距离站台C的路程和为5km.

查看试题解析
25. 如图，∠ABC＝45°，其中P、Q分别是射线BA、BC上的点，BP＝3 $\sqrt{2}$ .

(1)、给出条件①PQ＝4；②∠BPQ＝105°；③PQ＝6.能使BQ的长唯一确定的条件是；

(2)、在题（1）中选一个使BQ的长唯一确定的条件，求出此时BQ的长度.

查看试题解析
26. 如图，在△ABC中，∠C＝90°，以点C为圆心，CA长为半径的圆交AB于点D.

(1)、若∠B＝28°，求 $\overset{⌢}{A D}$ 的度数；

(2)、若D是AB的中点，AB＝2，求阴影部分的面积；

(3)、若AC＝ $\sqrt{3}$ ，求AD•AB的值.

查看试题解析
27. 定义：如果二次函数y＝a₁x²+b₁x+c₁（a₁≠0，a₁ ， b₁ ， c₁是常数）与y＝a₂x²+b₂x+c₂（a₂≠0，a₂ ， b₂ ， c₂是常数）满足a₁+a₂＝0，b₁＝b₂ ， c₁+c₂＝0，则这两个函数互为“N”函数.

(1)、写出y＝﹣x²+x﹣1的“N”函数的表达式；

(2)、若题（1）中的两个“N”函数与正比例函数y＝kx（k≠0）的图象只有两个交点，求k的值；

(3)、如图，二次函数y₁与y₂互为“N”函数，A、B分别是“N”函数y₁与y₂图象的顶点，C是“N”函数y₂与y轴正半轴的交点，连接AB、AC、BC，若点A（﹣2，1）且△ABC为直角三角形，求点C的坐标.

查看试题解析
28. 如图，在矩形ABCD中，AB＝4，BC＝4 $\sqrt{2}$ ，点P从点B出发沿BC方向运动，运动速度为每秒 $\sqrt{2}$ 个单位长度，点Q从点B同时出发，沿B﹣A﹣D方向运动，运动速度为每秒2个单位长度，当P到达点C时，两动点同时停止运动.设运动时间为ts，将矩形沿PQ所在直线翻折，B′是翻折后点B的对应点.

(1)、当t＝1时，PQ＝；

(2)、连接AC，若点B正好落在线段AC上，求t的值；

(3)、点B′能否落在AD所在直线上，若能，求出AB′的长度；若不能，请说明理由.

查看试题解析