山东省泰安市新泰市南部联盟2021-2022学年九年级上学期数学第一次月考试卷

试卷更新日期：2021-10-19 类型：月考试卷

进入出卷网下载

一、单选题

1. 下列函数中，不是反比例函数的是（）

A、y＝ $\frac{5}{x}$ B、y＝3x^－1 C、y＝ $\frac{x - 1}{7}$ D、xy＝ $\frac{3}{2}$

查看试题解析
2. 已知∠A为锐角，且tanA= $\sqrt{2}$ ，则∠A的取值范围是（　　）

A、0°＜∠A＜30° B、30°＜∠A＜45° C、45°＜∠A＜60° D、60°＜∠A＜90°

查看试题解析
3. 已知点 $A (x_{1} ， y_{1}) ， B (x_{2} ， y_{2})$ 是反比例函数 $y = \frac{2}{x}$ 图象上的点，若 $x_{1} > 0 > x_{2}$ ，则一定成立的是（）

A、 $y_{1} > y_{2} > 0$ B、 $y_{1} > 0 > y_{2}$ C、 $0 > y_{1} > y_{2}$ D、 $y_{2} > 0 > y_{1}$

查看试题解析
4. 如图，水库大坝截面的迎水坡AD的坡比为4：3，背水坡BC的坡比为1：2，大坝高DE＝20m ，坝顶宽CD＝10m ，则下底AB的长为（）

A、55m B、60m C、65m D、70m

查看试题解析
5. 将点P(4，3)向下平移1个单位长度后，落在函数y＝ $\frac{k}{x}$ 的图象上，则k的值为（）

A、k＝12 B、k＝10 C、k＝9 D、k＝8

查看试题解析
6. 如图，从点 $A$ 看一山坡上的电线杆 $P Q$ ，观测点 $P$ 的仰角是 $45 °$ ，向前走 $6 m$ 到达 $B$ 点，测得顶端点 $P$ 和杆底端点 $Q$ 的仰角分别是 $60 °$ 和 $30 °$ ，则该电线杆 $P Q$ 的高度（）

A、 $6 + 2 \sqrt{3}$ B、 $6 + \sqrt{3}$ C、 $10 - \sqrt{3}$ D、 $8 + \sqrt{3}$

查看试题解析
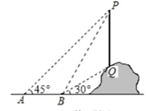7. 已知函数y＝ $\frac{k}{x}$ 中，当x＞0时，y随x增大而增大，那么函数y＝kx﹣k的大致图象为（）

A、 B、 C、 D、

查看试题解析
8. 如图，在Rt△ABC中，∠C＝90°，AB＝6，AC＝2，CD⊥AB于D ，设∠ACD＝α，则cosα的值为（）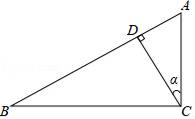

A、 $\frac{2 \sqrt{2}}{3}$ B、 $\frac{\sqrt{2}}{2}$ C、 $2 \sqrt{2}$ D、 $\frac{1}{3}$

查看试题解析
9. 如图，A，B是反比例函数y= $\frac{4}{x}$ 在第一象限内的图象上的两点，且A，B两点的横坐标分别是2和4，则△OAB的面积是（）

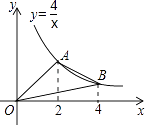A、4 B、3 C、2 D、1

查看试题解析
10. 如图，△ABC在网格(小正方形的边长均为1)中，则cos∠ABC的值是（）

A、 $\frac{3}{4}$ B、 $\frac{4}{3}$ C、 $\frac{3}{5}$ D、 $\frac{4}{5}$

查看试题解析
11.
双曲线 $y = \frac{10}{x}$ 与 $y = \frac{6}{x}$ 在第一象限内的图象如图所示，作一条平行于y轴的直线分别交双曲线于A、B两点，连接OA、OB，则△AOB的面积为
（）

A、1 B、2 C、3 D、4

查看试题解析
12. 如图，在△ABC中，∠A＝30°，E为AC上一点，且AE：EC＝3：1，EF⊥AB于F ，连接FC ，则tan∠CFB等于（）

A、 $\frac{1}{6} \sqrt{3}$ B、 $\frac{1}{2} \sqrt{3}$ C、 $\frac{4}{3} \sqrt{3}$ D、 $\frac{1}{4} \sqrt{3}$

查看试题解析

二、填空题

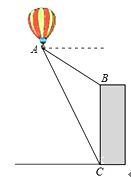
13. 已知函数 $y = (n + 1) x^{n^{2} - 5}$ 是反比例函数，且图象位于第一、三象限，则 $n =$ ．

查看试题解析
14. 在锐角△ABC中，若|cos²A﹣ $\frac{1}{4}$ |+（tanB﹣ $\sqrt{3}$ ）²＝0，则∠C的正切值是．

查看试题解析
15. 已知P₁(x₁ ， y₁)，P₂(x₂ ， y₂)两点都在反比例函数y＝﹣ $\frac{5}{x}$ 的图象上，且y₁＜y₂＜0，则x₁和x₂的大小关系是．

查看试题解析
16. 如图，热气球的探测器显示，从热气球A看一栋大楼顶部B的俯角为30°，看这栋大楼底部C的俯角为60°，热气球A的高度为270米，则这栋大楼的高度为米．

查看试题解析
17. 反比例函数y＝ $\frac{2}{x}$ 图象上三个点的坐标为(x₁ ， y₁)，(x₂ ， y₂)，(x₃ ， y₃)，若x₁＜x₂＜0＜x₃ ，则y₁ ， y₂ ， y₃的大小关系是．

查看试题解析
18. 如图，在Rt△ABC中，∠B＝90°，AB＝2 $\sqrt{5}$ ，BC＝ $\sqrt{5}$ .将△ABC绕点A按逆时针方向旋转90°得到△AB′C′，连结B′C，则sin ∠ACB′＝．

查看试题解析
19. 如图，点A在双曲线y＝ $\frac{1}{x}$ （x＞0）上，点B在双曲线y＝ $\frac{4}{x}$ （x＞0）上，且AB∥x轴，BC∥y轴，点C在x轴上，则△ABC的面积为．

查看试题解析
20. 如下图：直角三角形纸片的两直角边长分别为4，8，现将△ABC如图那样折叠，使点A与点B重合，折痕为DE，则 $\tan ∠ C B E$ 的值是．

查看试题解析

三、解答题

21. 计算：

(1)、 $\sqrt{3}$ cos30°+ $\sqrt{2}$ sin45°；

(2)、6tan²30°﹣ $\sqrt{3}$ sin 60°﹣2sin 45°．

查看试题解析
22. 已知反比例函数 $y = \frac{k - 1}{x}$ 的图象经过点 $A (- \sqrt{3} ， 1)$ ．

(1)、试确定此反比例函数的解析式；

(2)、设点 $B (- m + 1 ， n)$ 为图象上的一点，且 $n < 0$ ，求 $(m - 2) + | m - 1 |$ 值．

查看试题解析
23. 如图，某渔船向正东方向航行，在B处测得A岛在北偏东的45°方向，岛C在B处的正东方向且相距30海里，从岛C测得A岛在北偏西的60°方向，已知A岛周围8海里内有暗礁．如果渔船继续向东航行，有无触礁危险？（ $\sqrt{2}$ ≈1.4， $\sqrt{3}$ ≈1.7）

查看试题解析
24. 已知，如图，反比例函数y＝ $\frac{k}{x}$ 的图象与一次函数y＝ax+b的图象交于点A（1，4），点B（m ， ﹣1）．

(1)、求一次函数和反比例函数的解析式；

(2)、求△OAB的面积；

(3)、直接写出不等式ax+b≥ $\frac{k}{x}$ 的解集是．

查看试题解析
25. 如图，在△ABC中，∠C=90°，点D，E分别在AC，AB上，BD平分∠ABC，DE⊥AB于点E，AE=6，cosA= $\frac{3}{5}$ .

(1)、求CD的长；

(2)、求tan∠DBC的值.

查看试题解析
26. 如图，在平面直角坐标系中，OA⊥OB ， AB⊥x轴于点C ，点A（ $\sqrt{3}$ ，1）在反比例函数y＝ $\frac{k}{x}$ 的图象上．

(1)、求反比例函数y＝ $\frac{k}{x}$ 的表达式；

(2)、在x轴上是否存在一点P ，使得S_△AOP＝ $\frac{1}{2}$ S_△AOB ，若存在，求所有符合条件点P的坐标；若不存在，简述你的理由．

查看试题解析
27.
在某飞机场东西方向的地面l上有一长为1km的飞机跑道MN（如图），在跑道MN的正西端14.5千米处有一观察站A．某时刻测得一架匀速直线降落的飞机位于点A的北偏西30°，且与点A相距15千米的B处；经过1分钟，又测得该飞机位于点A的北偏东60°，且与点A相距5 $\sqrt{3}$ 千米的C处．

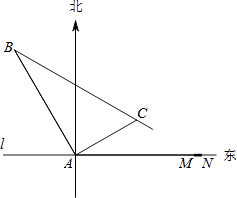(1)、该飞机航行的速度是多少千米/小时？（结果保留根号）

(2)、如果该飞机不改变航向继续航行，那么飞机能否降落在跑道MN之间？请说明理由．

查看试题解析