陕西省2021年中考数学模拟预测试卷
试卷更新日期:2021-10-19 类型:中考模拟
一、单选题
-
1. -2021的倒数是( )A、2021 B、 C、-2021 D、2. 下列四个图形中是三棱柱的表面展开图的是( )A、
 B、
B、 C、
C、 D、
D、 3. 将一块含30°角的直角三角板ABC(∠C=90°,∠B=30°)和一把直尺按如图所示的位置放置,若∠CED=43°,则∠BAF的度数为( )
3. 将一块含30°角的直角三角板ABC(∠C=90°,∠B=30°)和一把直尺按如图所示的位置放置,若∠CED=43°,则∠BAF的度数为( ) A、47° B、43° C、17° D、13°4. 《海岛算经》是我国杰出数学家刘徽留给后世最宝贵的数学遗产.书中的第一问:今有望海岛,立两表,齐高三丈,前后相去千步,令后表与前表参相直.从前表却行一百二十三步,人目着地取望岛峰,与表末参合.从后表却行一百二十七步,人目着地取望岛峰,亦与表末参合.问岛高及去表各几何?大致意思是:假设测量海岛,立两根表,高均为3丈,前后相距1000步,令后表与前表在同一直线上,从前表退行123步,人的眼睛贴着地面观察海岛,从后表退行127步,人的眼睛贴着地面观察海岛,问海岛高度及两表相距多远?想要解决这一问题,需要利用( )A、全等三角形 B、相似三角形 C、勾股定理 D、垂径定理5. 正比例函数 ,当自变量 的值增加2时,函数 的值( )A、减少10 B、增加10 C、减少 D、增加6. 在 中, , , 的平分线交 于点 ,若 ,则 长为( )A、 B、6 C、 D、87. 已知一次函数 ( 为常数)的图象经过 , ,若 , ,则 的值可能是( )A、-1 B、0 C、1 D、28. 如图,菱形 的对角线 , 交于点 ,过 作 于点 ,延长 交 于点 ,若 , ,则 的值为( )
A、47° B、43° C、17° D、13°4. 《海岛算经》是我国杰出数学家刘徽留给后世最宝贵的数学遗产.书中的第一问:今有望海岛,立两表,齐高三丈,前后相去千步,令后表与前表参相直.从前表却行一百二十三步,人目着地取望岛峰,与表末参合.从后表却行一百二十七步,人目着地取望岛峰,亦与表末参合.问岛高及去表各几何?大致意思是:假设测量海岛,立两根表,高均为3丈,前后相距1000步,令后表与前表在同一直线上,从前表退行123步,人的眼睛贴着地面观察海岛,从后表退行127步,人的眼睛贴着地面观察海岛,问海岛高度及两表相距多远?想要解决这一问题,需要利用( )A、全等三角形 B、相似三角形 C、勾股定理 D、垂径定理5. 正比例函数 ,当自变量 的值增加2时,函数 的值( )A、减少10 B、增加10 C、减少 D、增加6. 在 中, , , 的平分线交 于点 ,若 ,则 长为( )A、 B、6 C、 D、87. 已知一次函数 ( 为常数)的图象经过 , ,若 , ,则 的值可能是( )A、-1 B、0 C、1 D、28. 如图,菱形 的对角线 , 交于点 ,过 作 于点 ,延长 交 于点 ,若 , ,则 的值为( ) A、5 B、 C、 D、9. 如图,AB为 的直径,点C为AB上一点,点D在 上,AD=AC,连接DC并延长交 于点E,连接OE,若∠BAD=30°,则∠COE的度数为( )
A、5 B、 C、 D、9. 如图,AB为 的直径,点C为AB上一点,点D在 上,AD=AC,连接DC并延长交 于点E,连接OE,若∠BAD=30°,则∠COE的度数为( ) A、30° B、35° C、40° D、45°10. 若抛物线 ( 是常数)的图象经过第一、二、三象限,则 的取值范围是( )A、 B、 C、 D、
A、30° B、35° C、40° D、45°10. 若抛物线 ( 是常数)的图象经过第一、二、三象限,则 的取值范围是( )A、 B、 C、 D、二、填空题
-
11. 计算: .12. 计算: .13. 抛物线 的顶点坐标为.14. 如图,点 为正八边形 的中心,则 的度数为.
 15. 若反比例函数 ( )的图象与正比例函数 ( )的图象有两个交点 和 ,则 的值为.16. 我国是最早了解勾股定理的国家之一.如图,在 中, ,以其三边为边分别向外作正方形,即可证明勾股定理.连接 交 于点 ,连接 , .若 ,则 的值为.
15. 若反比例函数 ( )的图象与正比例函数 ( )的图象有两个交点 和 ,则 的值为.16. 我国是最早了解勾股定理的国家之一.如图,在 中, ,以其三边为边分别向外作正方形,即可证明勾股定理.连接 交 于点 ,连接 , .若 ,则 的值为.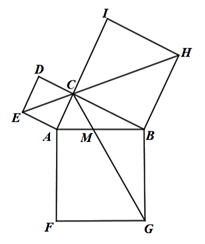
三、解答题
-
17. 解不等式组: .18. 解方程: .19. 如图,已知 ,点 在圆上,请以 为一顶点作圆内接正方形 .(保留作图痕迹,不写作法)
 20. 如图,在四边形 中, ,连接 ,点 在 上,连接 ,若 , ,求证: .
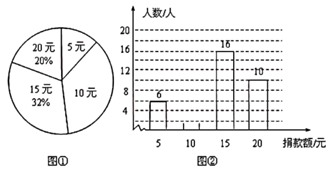
20. 如图,在四边形 中, ,连接 ,点 在 上,连接 ,若 , ,求证: . 21. 在一次“爱心助学”捐款活动中,全校同学人人拿出自己的零花钱,踊跃捐款,学生捐款额有5元、10元、15元、20元四种情况.刘老师在全校范围内随机抽取部分学生捐款数据,并根据统计数据绘制成图①和图②两幅尚不完整的统计图.
21. 在一次“爱心助学”捐款活动中,全校同学人人拿出自己的零花钱,踊跃捐款,学生捐款额有5元、10元、15元、20元四种情况.刘老师在全校范围内随机抽取部分学生捐款数据,并根据统计数据绘制成图①和图②两幅尚不完整的统计图.请你根据统计图提供的信息,回答下列问题:
 (1)、本次共抽取学生 ▲ 人,并请将图②的条形统计图补充完整;(2)、学生捐款的众数是 , 中位数是;(3)、若全校共有学生1260人,请你估计此次全校学生的捐款总额.22. 如图,图②是图①秋千的侧面示意图,秋千的静止状态为 ,已知 与地面平行, 、 是其在摆动过程中的两个位置,从 处测的 , 两点的俯角分别为65°和40°(即 , ),这时点 相对于点 秋千升高了 (即 ,其中 于 , 于 ),求该秋千摆绳 的长度.( , , , , , , , ,计算结果精确到 .)
(1)、本次共抽取学生 ▲ 人,并请将图②的条形统计图补充完整;(2)、学生捐款的众数是 , 中位数是;(3)、若全校共有学生1260人,请你估计此次全校学生的捐款总额.22. 如图,图②是图①秋千的侧面示意图,秋千的静止状态为 ,已知 与地面平行, 、 是其在摆动过程中的两个位置,从 处测的 , 两点的俯角分别为65°和40°(即 , ),这时点 相对于点 秋千升高了 (即 ,其中 于 , 于 ),求该秋千摆绳 的长度.( , , , , , , , ,计算结果精确到 .)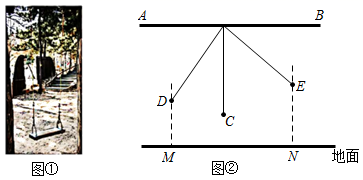 23. 为了做好新冠防疫工作,某学校开学前备足防疫物资,准备体温枪和消毒液若干,经市场调查:购买一把体温枪20元,一瓶消毒液5元,市场上现有甲,乙两所医疗机构.甲医疗机构销售方案为:购买一把体温枪送一瓶消毒液.乙医疗机构销售方案为:购买体温枪和消毒液全部打九折.若某学校准备购买50把体温枪,购买消毒液 瓶( ).(1)、分别写出按甲医疗机构销售方案购买费用 (元)、按乙医疗机构销售方案购买费用 (元)与购买消毒液 (瓶)之间的函数关系式;(2)、当 时,甲、乙两家医疗机构哪家购买费用比较合算.24. 刘老师将1个红球和若干个黄球放入一个不透明的口袋中并搅匀,这些球除颜色不同外其余都相同.他让若干学生进行摸球试验,每次摸出一个球,记下颜色后,放回搅匀,经过多次实验发现,从袋中摸出一个球是红球的频率稳定在0.25附近.(1)、估算袋中黄球的个数;(2)、在(1)的条件下,小强同学从中任意摸出一个球,放回并摇匀,再摸一次球,用画树状图或列表的方法计算他两次都摸出黄球的概率.25. 如图, 为 的直径, 为 延长线上一点,点 在 上,连接 , , ,作 于点 ,交 于点 ,若 .
23. 为了做好新冠防疫工作,某学校开学前备足防疫物资,准备体温枪和消毒液若干,经市场调查:购买一把体温枪20元,一瓶消毒液5元,市场上现有甲,乙两所医疗机构.甲医疗机构销售方案为:购买一把体温枪送一瓶消毒液.乙医疗机构销售方案为:购买体温枪和消毒液全部打九折.若某学校准备购买50把体温枪,购买消毒液 瓶( ).(1)、分别写出按甲医疗机构销售方案购买费用 (元)、按乙医疗机构销售方案购买费用 (元)与购买消毒液 (瓶)之间的函数关系式;(2)、当 时,甲、乙两家医疗机构哪家购买费用比较合算.24. 刘老师将1个红球和若干个黄球放入一个不透明的口袋中并搅匀,这些球除颜色不同外其余都相同.他让若干学生进行摸球试验,每次摸出一个球,记下颜色后,放回搅匀,经过多次实验发现,从袋中摸出一个球是红球的频率稳定在0.25附近.(1)、估算袋中黄球的个数;(2)、在(1)的条件下,小强同学从中任意摸出一个球,放回并摇匀,再摸一次球,用画树状图或列表的方法计算他两次都摸出黄球的概率.25. 如图, 为 的直径, 为 延长线上一点,点 在 上,连接 , , ,作 于点 ,交 于点 ,若 . (1)、求证: 是 的切线;(2)、若 , ,求 的长.26. 如图,在平面直角坐标系中,抛物线 的对称轴为直线 ,与 轴交于点 ,且经过点 .
(1)、求证: 是 的切线;(2)、若 , ,求 的长.26. 如图,在平面直角坐标系中,抛物线 的对称轴为直线 ,与 轴交于点 ,且经过点 . (1)、求抛物线 的表达式;(2)、连接 ,点 在线段 上,过 作 轴于 点,延长 交抛物线 于点 ,在直线 上取一点 ,使得 ≌ ,求满足条件的点 的坐标.27. 如图
(1)、求抛物线 的表达式;(2)、连接 ,点 在线段 上,过 作 轴于 点,延长 交抛物线 于点 ,在直线 上取一点 ,使得 ≌ ,求满足条件的点 的坐标.27. 如图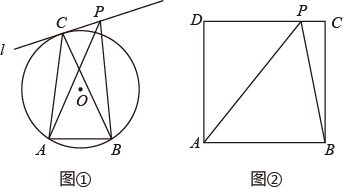
 (1)、问题提出:
(1)、问题提出:
如图①, 内接于 ,过点 作 的切线 ,在 上任取一个不同于点 的点 ,连接 、 ,比较 与 的大小,并说明理由.(2)、问题探究:
如图②,正方形 ,边长为2,在 边上是否存在点 ,使 最大?若存在,确定点 的位置,并求此时 的值;若不存在,请说明理由.(3)、问题解决:
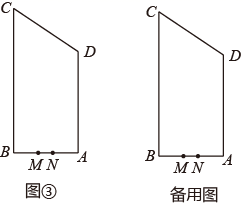
如图③,四边形 为某工作室的平面示意图,线段 、 、 为三面墙, 为入户门处,其中 , , , 米, 米, 米.出于安全考虑,负责人想在墙上安装监控装置 ,用来监控并记录进出的人员,为了让监控效果最佳,要求 最大.试问在墙上是否存在一点 ,使得 最大?若存在,请求出此时 的值及 点的位置;若不存在,请说明理由.