陕西省2021年数学中考复习诊断性试卷
试卷更新日期:2021-10-19 类型:中考模拟
一、单选题
-
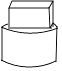
1. 计算(﹣2021)0的结果是( )A、﹣2021 B、2021 C、1 D、02. 如图所示的几何体是由一个长方体和一个圆柱体组成的,则它的主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 二次函数y=-2(x+1)2+3的图象的顶点坐标是( )A、(1,3) B、(-1,3) C、(1,-3) D、(-1,-3)4. 如图,已知 ,且 ,则 ( )
3. 二次函数y=-2(x+1)2+3的图象的顶点坐标是( )A、(1,3) B、(-1,3) C、(1,-3) D、(-1,-3)4. 如图,已知 ,且 ,则 ( ) A、 B、 C、 D、5. 变量 的一些对应值如下表:
A、 B、 C、 D、5. 变量 的一些对应值如下表:···
-2
-1
0
1
2
3
···
···
-8
-1
0
1
8
27
···
根据表格中的数据规律,当 时, 的值是( )
A、-64 B、64 C、-48 D、486. 如图,在 的网格中,每个小正方形的边长为 ,点 都在格点上,若将 绕 点顺时针旋转 得到 ,则 的长度为( ) A、 B、 C、 D、7. 平面直角坐标系中,直线 沿 轴向右平移 个单位后恰好经过 ,则 ( )A、-1 B、2 C、-4 D、-38. 如图,在正方形ABCD中,点E是BC延长线上的一点,且AC=EC,连接AE,交CD于点F,若AB=1,则线段DF的长是( )
A、 B、 C、 D、7. 平面直角坐标系中,直线 沿 轴向右平移 个单位后恰好经过 ,则 ( )A、-1 B、2 C、-4 D、-38. 如图,在正方形ABCD中,点E是BC延长线上的一点,且AC=EC,连接AE,交CD于点F,若AB=1,则线段DF的长是( )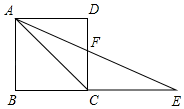 A、 B、 C、2﹣ D、 ﹣19. 如图, 是 的直径,点C、D在 上.若 ,则 的度数为( ).
A、 B、 C、2﹣ D、 ﹣19. 如图, 是 的直径,点C、D在 上.若 ,则 的度数为( ). A、25° B、30° C、35° D、40°10. 已知抛物线 与x轴相交于点A,B(点A在点B左侧),顶点为M.平移该抛物线,使点M平移后的对应点M'落在x轴上,点B平移后的对应点B'落在y轴上,则平移后的抛物线解析式为( )A、 B、 C、 D、
A、25° B、30° C、35° D、40°10. 已知抛物线 与x轴相交于点A,B(点A在点B左侧),顶点为M.平移该抛物线,使点M平移后的对应点M'落在x轴上,点B平移后的对应点B'落在y轴上,则平移后的抛物线解析式为( )A、 B、 C、 D、二、填空题
-
11. 已知实数 ,0.16, , , , ,其中为无理数的是.12. 已知正多边形的一个外角是72°,则这个正多边形的边数是.13. 若直线 和双曲线 交于 两点,那么 .14. 如图,在菱形 中, ,点 是菱形 内或边上的一点,且 ,连接 ,则 面积的最小值为.

三、解答题
-
15. 计算:16. 已知:如图,在 中, 是对角线 上两个点,且 .求证:
 17. 在 中, 为AB上一点,在 边上确定一点 .使 .(不写作法,保留作图痕迹)
17. 在 中, 为AB上一点,在 边上确定一点 .使 .(不写作法,保留作图痕迹) 18. 一天,小华爸爸开车带全家到西安游玩,实现爷爷奶奶想看大雁塔,游大唐芙蓉园的愿望,由导航可知,从小华家到西安大雁塔的路程为 ,他们全家早上 从家出发,途中他们在一个服务区短暂休息之后,继续行驶,在上午 时,他们距离西安大雁塔还有 ,如图是他们从家到西安大雁塔的过程中,行驶路程 与所用时间 之间的函数图象,请根据相关信息,解答下列问题:
18. 一天,小华爸爸开车带全家到西安游玩,实现爷爷奶奶想看大雁塔,游大唐芙蓉园的愿望,由导航可知,从小华家到西安大雁塔的路程为 ,他们全家早上 从家出发,途中他们在一个服务区短暂休息之后,继续行驶,在上午 时,他们距离西安大雁塔还有 ,如图是他们从家到西安大雁塔的过程中,行驶路程 与所用时间 之间的函数图象,请根据相关信息,解答下列问题: (1)、求小华一家在服务区休息了小时,上午 点时的速度为.(2)、求B 所在直线的函数表达式,并求小华一家这天几点到达西安大雁塔?19. 如图,为了测量山顶铁塔 的高,小明在27m高的楼 底部 测得塔顶A的仰角为 ,在楼顶 测得塔顶A的仰角 、已知山高 为 楼的底部 与山脚在同一水平线上,求该铁塔的高 .(参考数据: ).
(1)、求小华一家在服务区休息了小时,上午 点时的速度为.(2)、求B 所在直线的函数表达式,并求小华一家这天几点到达西安大雁塔?19. 如图,为了测量山顶铁塔 的高,小明在27m高的楼 底部 测得塔顶A的仰角为 ,在楼顶 测得塔顶A的仰角 、已知山高 为 楼的底部 与山脚在同一水平线上,求该铁塔的高 .(参考数据: ). 20. 某年级共有300名学生.为了解该年级学生A,B两门课程的学习情况,从中随机抽取60名学生进行测试,获得了他们的成绩(百分制),并对数据(成绩)进行整理、描述和分析.下面给出了部分信息.
20. 某年级共有300名学生.为了解该年级学生A,B两门课程的学习情况,从中随机抽取60名学生进行测试,获得了他们的成绩(百分制),并对数据(成绩)进行整理、描述和分析.下面给出了部分信息..A课程成绩的频数分布直方图如下(数据分成6组: , , , , , );
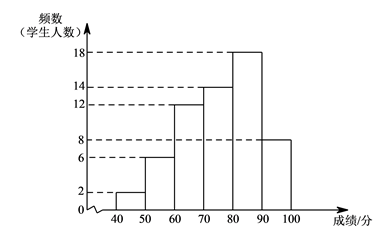
.A课程成绩在 这一组是:
70 71 71 71 76 76 77 78 79 79 79
.A,B两门课程成绩的平均数、中位数、众数如下:
课程
平均数
中位数
众数
A
B
70
83
根据以上信息,回答下列问题:
(1)、写出表中 的值;(2)、在此次测试中,某学生的A课程成绩为76分,B课程成绩为71分,这名学生成绩排名更靠前的课程是(填“A”或“B”),理由是;(3)、假设该年级学生都参加此次测试,估计A课程成绩超过 分的人数.21. 为弘扬中华传统文化,黔南州近期举办了中小学生“国学经典大赛”.比赛项目为:A.唐诗;B.宋词;C.论语;D.三字经.比赛形式分“单人组”和“双人组”.(1)、小丽参加“单人组”,她从中随机抽取一个比赛项目,恰好抽中“三字经”的概率是多少?(2)、小红和小明组成一个小组参加“双人组”比赛,比赛规则是:同一小组的两名队员的比赛项目不能相同,且每人只能随机抽取一次,则恰好小红抽中“唐诗”且小明抽中“宋词”的概率是多少?请用画树状图或;列表的方法进行说明.22. 如图, 是 的直径,点 是 上一点, 的平分线 交 于点 ,过点 作 交 的延长线于点 . (1)、求证: 是 的切线;(2)、过点 作 于点 ,连接 .若 , ,求 的长度.23. 如图,抛物线 经过 三点.
(1)、求证: 是 的切线;(2)、过点 作 于点 ,连接 .若 , ,求 的长度.23. 如图,抛物线 经过 三点. (1)、求抛物线的表达式.(2)、抛物线的顶点 与对称轴 上的点 关于 轴对称,直线 交抛物线于点 ,直线 交 于点 ,若直线 将 的面积分为 的两部分,求点 的坐标.24. 如图
(1)、求抛物线的表达式.(2)、抛物线的顶点 与对称轴 上的点 关于 轴对称,直线 交抛物线于点 ,直线 交 于点 ,若直线 将 的面积分为 的两部分,求点 的坐标.24. 如图 (1)、问题发现:
(1)、问题发现:
如图1, 内接于半径为4的 ,若 ,则 ;(2)、问题探究:
如图2,四边形 内接于半径为6的 ,若 ,求四边形 的面积最大值;(3)、解决问题:
如图3,一块空地由三条直路(线段 、AB、 )和一条弧形道路 围成,点 是 道路上的一个地铁站口,已知 千米, 千米, , 的半径为1千米,市政府准备将这块空地规划为一个公园,主入口在点 处,另外三个入口分别在点 、 、 处,其中点 在 上,并在公园中修四条慢跑道,即图中的线段 、 、 、 ,是否存在一种规划方案,使得四条慢跑道总长度(即四边形 的周长)最大?若存在,求其最大值;若不存在,说明理由.