广东省肇庆市四会市三校联考2021-2022学年九年级上学期数学第一次月考试卷
试卷更新日期:2021-10-19 类型:月考试卷
一、单选题
-
1. 下列函数中,属于二次函数的是( )A、 B、 C、 D、2. 若关于 的方程 有一个根为2.则另一个根为( )A、-2 B、2 C、4 D、-33. 在平面直角坐标系中,将二次函数 的图像向左平移2个单位长度,再向上平移1个单位长度,所得抛物线对应的函数表达式为( )A、 B、 C、 D、4. 已知关于x的一元二次方程ax2﹣4x﹣2=0有实数根,则a的取值范围是( )A、a≥﹣2 B、a>﹣2 C、a≥﹣2且a≠0 D、a>﹣2且a≠05. 三角形两边的长是3和4,第三边的长是方程x2-12x+35=0的根,则该三角形的周长为( )A、12 B、14 C、12或14 D、246. 如表是二次函数y=ax2+bx+c的几组对应值:
x
6.17
6.18
6.19
6.20
y=ax2+bx+c
﹣0.03
﹣0.01
0.02
0.04
根据表中数据判断,方程ax2+bx+c=0的一个解x的范围是( )
A、6<x<6.17 B、6.17<x<6.18 C、6.18<x<6.19 D、6.19<x<6.207. 若实数k、b是一元二次方程 的两个根,且 ,则一次函数 的图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限8. 某校九年级(1)班学生毕业时,每个同学都将自己的相片向全班其他同学各送一张留作纪念,全班共送了1980张相片,如果全班有x名学生,根据题意,列出方程为( )A、 B、x(x+1)=1980 C、2x(x+1)=1980 D、x(x-1)=19809. 在同一平面直角坐标系中,二次函数 与一次函数 的图象如图所示,则二次函数 的图象可能是( )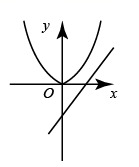 A、
A、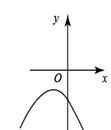 B、
B、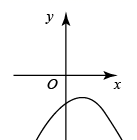 C、
C、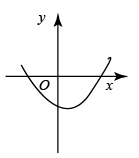 D、
D、 10. 已知二次函数 的图象如图所示,给出以下结论:① ;② ;③ ;④ ;⑤ .其中结论正确的个数有
10. 已知二次函数 的图象如图所示,给出以下结论:① ;② ;③ ;④ ;⑤ .其中结论正确的个数有 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
11. 一元二次方程x2﹣3x=0的解是 .12. 抛物线 的顶点坐标是.13. 若关于 的一元二次方程 的一根是0,则 =.14. 若点A(﹣2,y1)和B(1,y2)是二次函数y=x2﹣4x﹣3图象上的两点,则y1y2.(填“<”“=”或“>”)15. 若 是方程 一个根,则代数式 的值为.16. 如图,抛物线 与直线 的两个交点坐标分别为 , ,则方程 的解是.
 17. 如图,抛物线 在第一象限内经过的整数点 横坐标、纵坐标都为整数的点 依次为 , , , 其中 的横坐标为1将抛物线 沿直线L: 平移得一系列抛物线,且同时满足下列两个条件: 抛物线的顶点 , , , , 都在直线L: 上; 抛物线依次经过点 , , , 则顶点 的坐标为
17. 如图,抛物线 在第一象限内经过的整数点 横坐标、纵坐标都为整数的点 依次为 , , , 其中 的横坐标为1将抛物线 沿直线L: 平移得一系列抛物线,且同时满足下列两个条件: 抛物线的顶点 , , , , 都在直线L: 上; 抛物线依次经过点 , , , 则顶点 的坐标为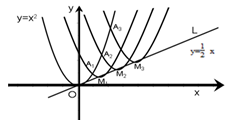
三、解答题
-
18.(1)、解方程:2x2+1=3x;(2)、将二次函数 配方成y=a(x﹣h)2+k的形式.19. 二次函数图象的顶点坐标是(-2,3),并经过点(1,2),求这个二次函数的函数关系式.20. 已知抛物线y=-2x2+(m-3)x-8.(1)、若抛物线的对称轴为y轴,求m的值;(2)、若抛物线的顶点在x正半轴上,求m的值.21. 关于x的一元二次方程 有两个实数根 , .(1)、求k的取值范围;(2)、是否存在实数k , 使得 和 互为相反数?若存在,请求出k的值;若不存在,请说明理由.22. 如图,矩形ABCD , AB=6cm , AD=2cm , 点P以2cm/s的速度从顶点A出发沿折线A-B-C向点C运动,同时点Q以lcm/s的速度从顶点C出发向点D运动,当其中一个动点到达末端停止运动时,另一点也停止运动.
 (1)、问两动点运动几秒,使四边形PBCQ的面积是矩形ABCD面积的 ;(2)、问两动点经过多长时间使得点P与点Q之间的距离为 ?若存在,
(1)、问两动点运动几秒,使四边形PBCQ的面积是矩形ABCD面积的 ;(2)、问两动点经过多长时间使得点P与点Q之间的距离为 ?若存在,求出运动所需的时间;若不存在,请说明理由.
23. 如图,直线y=﹣x+2过x轴上的点A(2,0),且与抛物线y=ax2交于B,C两点,点B坐标为(1,1).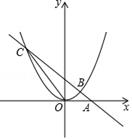 (1)、求抛物线的函数表达式;(2)、连结OC,求出△AOC的面积.(3)、当 -x+2>ax2 时,请观察图像直接写出x的取值范围.24. 某超市经销一种商品,每件成本为50元.经市场调研,当该商品每件的销售价为60元时,每个月可销售300件,若每件的销售价每增加1元,则每个月的销售量将减少10件.设该商品每件的销售价为x元,每个月的销售量为y件.(1)、求y与x的函数表达式;(2)、当该商品每件的销售价为多少元时,每个月的销售利润最大?最大利润是多少?25. 将抛物线y=ax2(a≠0)向左平移1个单位,再向上平移4个单位后,得到抛物线H:y=a(x﹣h)2+k.抛物线H与x轴交于点A,B,与y轴交于点C.已知A(﹣3,0),点P是抛物线H上的一个动点.
(1)、求抛物线的函数表达式;(2)、连结OC,求出△AOC的面积.(3)、当 -x+2>ax2 时,请观察图像直接写出x的取值范围.24. 某超市经销一种商品,每件成本为50元.经市场调研,当该商品每件的销售价为60元时,每个月可销售300件,若每件的销售价每增加1元,则每个月的销售量将减少10件.设该商品每件的销售价为x元,每个月的销售量为y件.(1)、求y与x的函数表达式;(2)、当该商品每件的销售价为多少元时,每个月的销售利润最大?最大利润是多少?25. 将抛物线y=ax2(a≠0)向左平移1个单位,再向上平移4个单位后,得到抛物线H:y=a(x﹣h)2+k.抛物线H与x轴交于点A,B,与y轴交于点C.已知A(﹣3,0),点P是抛物线H上的一个动点.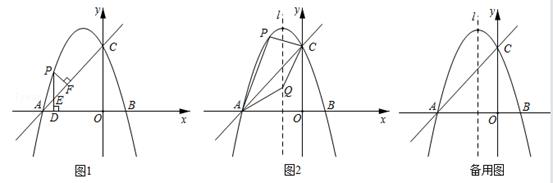 (1)、求抛物线H的表达式;(2)、如图1,点P在线段AC上方的抛物线H上运动(不与A,C重合),过点P作PD⊥AB,垂足为D,PD交AC于点E.作PF⊥AC,垂足为F,求△PEF的面积的最大值;(3)、如图2,点Q是抛物线H的对称轴l上的一个动点,在抛物线H上,是否存在点P,使得以点A,P,C,Q为顶点的四边形是平行四边形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由.
(1)、求抛物线H的表达式;(2)、如图1,点P在线段AC上方的抛物线H上运动(不与A,C重合),过点P作PD⊥AB,垂足为D,PD交AC于点E.作PF⊥AC,垂足为F,求△PEF的面积的最大值;(3)、如图2,点Q是抛物线H的对称轴l上的一个动点,在抛物线H上,是否存在点P,使得以点A,P,C,Q为顶点的四边形是平行四边形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由.