广东省湛江市吴川市三校联考2021-2022学年九年级上学期数学第一次月考试卷

试卷更新日期：2021-10-19 类型：月考试卷

进入出卷网下载

一、单选题

1. 用配方法解方程 $x^{2} - 4 x = 1$ 时，原方程应变形为（）

A、 ${(x - 2)}^{2} = 1$ B、 ${(x + 2)}^{2} = 5$ C、 ${(x + 2)}^{2} = 1$ D、 ${(x - 2)}^{2} = 5$

查看试题解析

2. 观察下列表格，一元二次方程x²﹣x＝1.1的一个解x所在的范围是（）

x	1.1	1.2	1.3	1.4	1.5	1.6	1.7	1.8	1.9
x²﹣x	0.11	0.24	0.39	0.56	0.75	0.96	1.19	1.44	1.71

A、1.5＜x＜1.6 B、1.6＜x＜1.7 C、1.7＜x＜1.8 D、1.8＜x＜1.9

查看试题解析

3. 关于x的方程 $x^{2} ﹣ 2 x + a = 0$ （a为常数）无实数根，则点 $(a ， a + 1)$ 在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
4. 将抛物线 $y = 2 x^{2} - 2$ 的向右平移1个单位长度，再向下平移3个单位长度后，得到抛物线的解析式是（）

A、 $y = 2 {(x + 1)}^{2} + 1$ B、 $y = 2 {(x + 1)}^{2} - 5$ C、 $y = 2 {(x - 1)}^{2} + 5$ D、 $y = 2 {(x - 1)}^{2} + 1$

查看试题解析
5. 已知三角形的两边长为4和5，第三边的长是方程x²﹣5x+6＝0的一个根，则这个三角形的周长是（）

A、11 B、12 C、11或12 D、15

查看试题解析
6. 如图所示，二次函数 $y = - x^{2} + 2 x + k$ 的图像与x轴的一个交点坐标为 $(3 ， 0)$ ，则关于 $x$ 的一元二次方程 $- x^{2} + 2 x + k = 0$ 的解为（）

A、 $x_{1} = 3 ， x_{2} = - 2$ B、 $x_{1} = 3 ， x_{2} = - 1$ C、 $x_{1} = 1 ， x_{2} = - 1$ D、 $x_{1} = 3 ， x_{2} = - 3$

查看试题解析
7. 某公司今年1月的营业额为250万元，按计划第1季度的营业额要达到900万元，设该公司2、3月的营业额的月平均增长率为 $x$ ．根据题意列方程正确的是（）

A、 $250 {(1 + x)}^{2} = 900$ B、 $250 {(1 + x %)}^{2} = 900$ C、 $250 (1 + x) + 250 {(1 + x)}^{2} = 900$ D、 $250 + 250 (1 + x) + 250 {(1 + x)}^{2} = 900$

查看试题解析
8. 下列对二次函数 $y = x^{2} - x$ 的图像的描述，正确的是（）

A、开口向下 B、对称轴是y轴 C、顶点坐标为 $(\frac{1}{2}, - \frac{1}{4})$ D、在对称轴右侧部分，y随x的增大而减小

查看试题解析
9. 在同一平面直角坐标系中，函数 $y = a x^{2} + b x + 2 b$ 与 $y = - a x + b$ 的图象可能是（）

A、 B、 C、 D、

查看试题解析
10. 如图所示，已知二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图像与 $x$ 轴交于 $(x_{1} ， 0)$ ，且 $- 1 < x_{1} < 0$ ，对称轴 $x = 1$ ．有下列5个结论：① $a b c > 0$ ；② $b < a + c$ ；③ $4 a + 2 b + c > 0$ ；④ $2 c > 3 b$ ；⑤ $a + b > m (a m + b)$ （ $m$ 是不等于1的实数）．其中结论正确的个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 二次函数y＝ $\frac{1}{2}$ （x﹣1）²﹣1的顶点坐标是．

查看试题解析
12. 已知 $a$ ， $b$ 为一元二次方程 $x^{2} + 2 x - 9 = 0$ 的两根，那么 $a^{2} + a - b$ 的值为.

查看试题解析
13. 已知等腰 $△$ ABC的三条边长都是方程x²-9x+18=0的根，则 $△$ ABC的周长为；

查看试题解析
14. 波音公司生产某种型号飞机，7月份的月产量为50台，由于改进了生产技术，计划9月份生产飞机98台，那么8、9月飞机生产量平均每月的增长率是．

查看试题解析
15. 对于任意实数 $a$ ，抛物线 $y = x^{2} + 2 a x + a + b$ 与 $x$ 轴都有公共点.则 $b$ 的取值范围是.

查看试题解析
16. 抛物线经过坐标系（-1，0）和（0，3）两点，对称轴 $x = 1$ ，如图所示，则当 $y < 0$ 时，x的取值范围是．

查看试题解析
17. 二次函数 $y = {ax}^{2} + bx + c (a \neq 0)$ 图象如图，下列结论：
① $abc > 0$ ；② $2 a + b = 0$ ；③当 $x \neq 1$ 时， $a + b > {ax}^{2} + bx$ ；④ $a - b + c > 0$ ．

其中正确的有．

查看试题解析

三、解答题

18.

(1)、解方程：2x²﹣4x﹣6=0．

(2)、①直接写出函数y=2x²﹣4x﹣6的图象与x轴交点坐标；
②求函数y=2x²﹣4x﹣6的图象的顶点坐标．

查看试题解析
19. 已知二次函数的图象的顶点为 $(1, - 3)$ ，且过点 $P (2, 0)$ ，求这个二次函数的解析式.

查看试题解析
20. 已知关于的方程 $x^{2} + 2 x + m - 2 = 0$ ．

(1)、若该方程有两个不相等的实数根，求实数m的取值范围；

(2)、当该方程的一个根为1时，求m的值及方程的另一根．

查看试题解析
21. 劳动是财富的源泉，也是幸福的源泉．某中学对劳动教育进行积极探索和实践，创建学生劳动教育地，让学生参与到农耕劳作中．如图，现准备利用校园围墙的一段 $M N$ （ $M N$ 最长可用 $25 m$ ），用 $40 m$ 长的篱笆，围成一个矩形菜园 $A B C D$ ．

(1)、当AB长度为多少时，矩形菜园的面积为 $150 m^{2}$ ？

(2)、能否围成面积为 $210 m^{2}$ 的矩形菜园？为什么？

查看试题解析
22. 已知，如图所示，直线l经过点A（4，0）和B（0，4），它与抛物线y＝ax²在第一象限内交于点P，又△AOP的面积为 $\frac{9}{2}$ ，求a的值．

查看试题解析
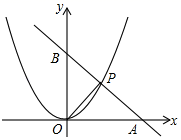23. 某商家销售一款商品，该商品的进价为每件80元，现在的售价为每件145元，每天可销售40件商场规定每销售一件需支付给商场管理费5元，通过市场调查发现，该商品单价每降1元，每天销售量增加2件若每件商品降价x元，每天的利润为y元，请完成以下问题的解答．

(1)、用含x的式子表示：①每件商品的售价为元；②每天的销售量为件；

(2)、求出 $y$ 与 $x$ 之间的函数关系式，并求出售价为多少时利润最大？最大利润是多少元？

查看试题解析
24. 在平面直角坐标系 $x O y$ 中，抛物线 $y = a x^{2} - 4 a x + 1$ .

(1)、若抛物线过点 $A (- 1, 6)$ ，求二次函数的表达式；

(2)、指出（1）中x为何值时y随x的增大而减小；

(3)、若直线 $y = m$ 与（1）中抛物线有两个公共点，求m的取值范围.

查看试题解析
25. 如图，抛物线 $y = a x^{2} - 6 x + c$ 交x轴于 $A ， B$ 两点，交y轴于点C.直线 $y = - x + 5$ 经过点B（5，0），C（0，5）

(1)、求抛物线的解析式；

(2)、抛物线的对称轴直线 $l$ 与直线 $B C$ 相交于点P，连接 $A C ， A P$ ，判定 $Δ A P C$ 的形状，并说明理由；

(3)、在直线 $B C$ 上是否存在点M，使 $A M$ 与直线 $B C$ 的夹角等于 $∠ A C B$ 的2倍？若存在，请求出点M的坐标；若不存在，请说明理由.

查看试题解析