广东省汕头市潮阳区三校联考2021-2022学年九年级上学期数学第一次月考试卷
试卷更新日期:2021-10-19 类型:月考试卷
一、单选题
-
1. 关于 的一元二次方程 有两个实数根,则 的取值范围是( )A、 B、 C、 且 D、 且2. 把方程x2﹣8x﹣84=0化成(x+m)2=n的形式为( )A、(x﹣4)2=100 B、(x﹣16)2=100 C、(x﹣4)2=84 D、(x﹣16)2=843. 将二次函数 的图象向左平移1个单位长度,再向上平移2个单位后,所得图象的函数解析式是( )A、 B、 C、 D、4. 下列图形既是中心对称又是轴对称的是( )A、
 B、
B、 C、
C、 D、
D、 5. 定义新运算“a※b”:对于任意实数a、b,都有a※b=(a+b)(a﹣b)﹣1,例4※2=(4+2)(4﹣2)﹣1=12﹣1=11.则方程x※1=x的根的情况为( )A、无实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、只有一个实数根6. 三角形两边的长是3和4,第三边的长是方程 的根,则该三角形的周长为( )A、10 B、12 C、14 D、12或147. 下表中列出的是一个二次函数的自变量x与函数y的几组对应值:
5. 定义新运算“a※b”:对于任意实数a、b,都有a※b=(a+b)(a﹣b)﹣1,例4※2=(4+2)(4﹣2)﹣1=12﹣1=11.则方程x※1=x的根的情况为( )A、无实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、只有一个实数根6. 三角形两边的长是3和4,第三边的长是方程 的根,则该三角形的周长为( )A、10 B、12 C、14 D、12或147. 下表中列出的是一个二次函数的自变量x与函数y的几组对应值:…
-2
0
1
3
…
…
6
-4
-6
-4
…
下列各选项中,正确的是
A、这个函数的图象开口向下 B、这个函数的图象与x轴无交点 C、这个函数的最小值小于-6 D、当 时,y的值随x值的增大而增大8. 近年来某县加大了对教育经费的投入,2019年投入2500万元,2021 年预计投入3500万元。假设该县投入教育经费的年平均增长率为x,根据题意列方程。则下列方程正确的是( )A、2500x2=3500 B、2500(1+x)2=3500 C、2500 (1+x%)2=3500 D、2500(1+x)+2500(1+x)2=35009. 在同一平面直角坐标系中,二次函数 与一次函数 的图象如图所示,则二次函数 的图象可能是( )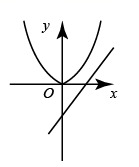 A、
A、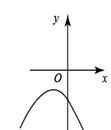 B、
B、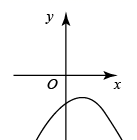 C、
C、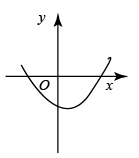 D、
D、 10. 已知二次函数 的图像如图所示,有下列结论:① ;② >0;③ ;④不等式 <0的解集为1≤ <3,正确的结论个数是( )
10. 已知二次函数 的图像如图所示,有下列结论:① ;② >0;③ ;④不等式 <0的解集为1≤ <3,正确的结论个数是( ) A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
11. 抛物线 的顶点坐标为 .12. 已知m2+m﹣1=0,则m3+2m2+2014=.13. 已知点 都在抛物线 上,若 ,则 .(填“>”、“<”或“=”)14. 如图,抛物线 与直线 的两个交点坐标分别为 , ,则方程 的解是.
 15. 二次函数y=x2﹣2x+m的最小值为2,则m的值为 .16. 如图,在△ABC中,∠B=90°,AB=12cm , BC=24cm , 动点P从点A开始向B点以2cm/s的速度移动(不与点B重合);动点Q从点B开始向点C以4cm/s的速度移动(不与点C重合).如果P、Q分别从A、B同时出发,那么经过秒四边形APQC的面积最小.
15. 二次函数y=x2﹣2x+m的最小值为2,则m的值为 .16. 如图,在△ABC中,∠B=90°,AB=12cm , BC=24cm , 动点P从点A开始向B点以2cm/s的速度移动(不与点B重合);动点Q从点B开始向点C以4cm/s的速度移动(不与点C重合).如果P、Q分别从A、B同时出发,那么经过秒四边形APQC的面积最小.
三、解答题
-
17. 若关于x的方程 的一个根是1,则另一个根是 .18. 解下列方程:(1)、x2﹣4x=0;(2)、2y2+4y=519. 请把二次函数 化为顶点式 的形式.并写出抛物线的开口方向,对称轴和顶点坐标.20. 校园空地上有一面墙,长度为20m,用长为32m的篱笆和这面墙围成一个矩形花圃,如图所示.
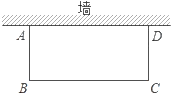 (1)、能围成面积是126m2的矩形花圃吗?若能,请举例说明;若不能,请说明理由.(2)、若篱笆再增加4m,围成的矩形花圃面积能达到170m2吗?请说明理由.21. 如图,一架长5米的梯子AB,顶端B靠在墙上,梯子底端A到墙的距离AC=3米.
(1)、能围成面积是126m2的矩形花圃吗?若能,请举例说明;若不能,请说明理由.(2)、若篱笆再增加4m,围成的矩形花圃面积能达到170m2吗?请说明理由.21. 如图,一架长5米的梯子AB,顶端B靠在墙上,梯子底端A到墙的距离AC=3米. (1)、求BC的长;(2)、梯子滑动后停在DE的位置,当AE为多少时,AE与BD相等?22. 某市场销售一批名牌衬衫,平均每天可销售20件,每件赢利40元.为了扩大销售,增加赢利,尽快减少库存,商场决定采取适当降价措施.经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件.求:(1)、若商场平均每天赢利1200元,且让顾客得到实惠,每件衬衫应降价多少元?(2)、要使商场平均每天赢利最多,请你帮助设计方案.
(1)、求BC的长;(2)、梯子滑动后停在DE的位置,当AE为多少时,AE与BD相等?22. 某市场销售一批名牌衬衫,平均每天可销售20件,每件赢利40元.为了扩大销售,增加赢利,尽快减少库存,商场决定采取适当降价措施.经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件.求:(1)、若商场平均每天赢利1200元,且让顾客得到实惠,每件衬衫应降价多少元?(2)、要使商场平均每天赢利最多,请你帮助设计方案.
23. 关于x的一元二次方程 有两个实数根 , .(1)、求k的取值范围;(2)、是否存在实数k , 使得 和 互为相反数?若存在,请求出k的值;若不存在,请说明理由.24. 已知抛物线 的图象如图所示,它与 轴的一个交点的坐标为 ,与 轴的交点坐标为 . (1)、求抛物线的解析式及与 轴的另一个交点 的坐标;(2)、根据图象回答:当 取何值时, ?(3)、在抛物线的对称轴上有一动点 ,求 的值最小时的点 的坐标.25. 如图,在平面直角坐标系中,抛物线 与x轴交于点 , ,与y轴交于点C.
(1)、求抛物线的解析式及与 轴的另一个交点 的坐标;(2)、根据图象回答:当 取何值时, ?(3)、在抛物线的对称轴上有一动点 ,求 的值最小时的点 的坐标.25. 如图,在平面直角坐标系中,抛物线 与x轴交于点 , ,与y轴交于点C. (1)、求该抛物线的解析式;(2)、直线l为该抛物线的对称轴,点D与点C关于直线l对称,点P为直线AD下方抛物线上一动点,连接PA,PD,求 面积的最大值;(3)、在(2)的条件下,将抛物线 沿射线AD平移 个单位,得到新的抛物线 ,点E为点P的对应点,点F为 的对称轴上任意一点,在 上确定一点G,使得以点D,E,F,G为顶点的四边形是平行四边形,写出所有符合条件的点G的坐标,并任选其中一个点的坐标,写出求解过程.
(1)、求该抛物线的解析式;(2)、直线l为该抛物线的对称轴,点D与点C关于直线l对称,点P为直线AD下方抛物线上一动点,连接PA,PD,求 面积的最大值;(3)、在(2)的条件下,将抛物线 沿射线AD平移 个单位,得到新的抛物线 ,点E为点P的对应点,点F为 的对称轴上任意一点,在 上确定一点G,使得以点D,E,F,G为顶点的四边形是平行四边形,写出所有符合条件的点G的坐标,并任选其中一个点的坐标,写出求解过程.