河南省南阳市中原名校2020-2021学年数学中考第二次大联考试卷
试卷更新日期:2021-10-19 类型:中考模拟
一、单选题
-
1. ﹣2的绝对值是( )A、2 B、 C、 D、-22. 2021年3月5日,李克强总理在政府工作报告中指出,过去五年,我国国民生产总值从不到70万亿元增加到了100万亿元.100万亿用科学记数法表示正确的是( )A、 B、 C、 D、3. 下列计算正确的是( )A、 B、 C、 D、4. 在体育模拟测试中,某班10名学生的成绩分别是60,58,62,66,68,66,67,63,69,65,这组数据的众数和中位数分别是( )A、66,65 B、66, C、66,66 D、66,675. 如图, , 平分 交 于点 .若 ,则 的度数为( )
 A、36° B、41° C、46° D、51°6. 下列关于二次函数 的说法正确的是( )A、该函数图象的开口向上 B、该函数图象的顶点坐标为 C、当 时, 随 的增大而减小 D、该函数的最大值为77. 某校初三年级举行班级篮球友谊赛,每两个班都要进行一场比赛,张老师告诉小丽总共要进行120场比赛,小丽想通过列方程求出参与比赛的班级数.设参与比赛的班级有 个,则所列方程正确的是( )A、 B、 C、 D、8. 如图,四边形 中, , , ,点 , 分别是对角线 , 的中点,则 的长为( )
A、36° B、41° C、46° D、51°6. 下列关于二次函数 的说法正确的是( )A、该函数图象的开口向上 B、该函数图象的顶点坐标为 C、当 时, 随 的增大而减小 D、该函数的最大值为77. 某校初三年级举行班级篮球友谊赛,每两个班都要进行一场比赛,张老师告诉小丽总共要进行120场比赛,小丽想通过列方程求出参与比赛的班级数.设参与比赛的班级有 个,则所列方程正确的是( )A、 B、 C、 D、8. 如图,四边形 中, , , ,点 , 分别是对角线 , 的中点,则 的长为( )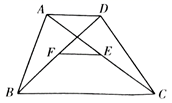 A、1 B、1.5 C、2.5 D、3.59. 如图,点 , 都在反比例函数 的图象上, 的延长线交 轴于点 .已知 , 的面积为6,则 的值为( )
A、1 B、1.5 C、2.5 D、3.59. 如图,点 , 都在反比例函数 的图象上, 的延长线交 轴于点 .已知 , 的面积为6,则 的值为( )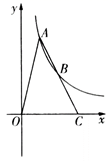 A、2 B、3 C、4 D、510. 如图,等边三角形 中, ,点 在边 上,且 ,点 是边 上的一动点,作射线 .射线 绕点 顺时针旋转60°得到射线 ,交 于点 ,则点 从 的运动过程中, 的最大值是( )
A、2 B、3 C、4 D、510. 如图,等边三角形 中, ,点 在边 上,且 ,点 是边 上的一动点,作射线 .射线 绕点 顺时针旋转60°得到射线 ,交 于点 ,则点 从 的运动过程中, 的最大值是( )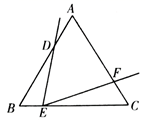 A、 B、1 C、 D、
A、 B、1 C、 D、二、填空题
-
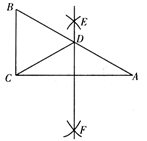
11. 计算: .12. 不等式 的最小整数解是.13. 如图, 的三个内角满足 .分别以点 , 为圆心,大于 的长为半径作弧,两弧交于点 , ,作直线 交 于点 ,连接 .若 ,则 .
 14. 五张完全相同的卡片上分别写有数字1, , ,2, .闭上眼睛洗匀后随机抽取三张,以卡片上的数字作为三角形的三边,所得三角形恰好是直角三角形的概率为.15. 如图,在平面直角坐标系中, , ,以 为斜边作等腰直角三角形 ,则点 的坐标为.
14. 五张完全相同的卡片上分别写有数字1, , ,2, .闭上眼睛洗匀后随机抽取三张,以卡片上的数字作为三角形的三边,所得三角形恰好是直角三角形的概率为.15. 如图,在平面直角坐标系中, , ,以 为斜边作等腰直角三角形 ,则点 的坐标为.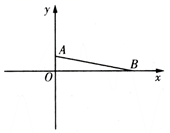
三、解答题
-
16. 先化简,再求值: ,其中 .17. 近几年,研学旅行已成为中小学广泛开展的课外拓展活动.某学校认真策划研学旅行活动,有针对性地开发了自然、历史、地理、科技、人文、体验等六种类型的活动课程.为了了解同学们选择课程的情况,校园小记者随机调查了本校部分同学,根据调查结果绘制出了如下两个尚不完整的统计图.

请结合图中所给信息,解答下列问题:
(1)、这次被调查的学生共有人;(2)、求扇形统计图中“历史”所对应的圆心角的度数,并补全条形统计图;(3)、若全校共有5000人,请你估计选择“体验”类课程的学生人数.18. 位于河南省登封市境内的嵩岳寺塔是中国现存最早的砖塔,反映了中外建筑文化交流融合创新的历程,在结构、造型等方面具有很大价值,对后世砖塔建筑有着巨大影响.
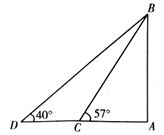
清明假期,小红利用所学知识来测量塔的高度,测角仪和塔底 在同一水平面,如图,她先在 处测得塔顶 的仰角为57°,然后沿直线 向远离塔的方向前进20米到达 处,测得塔顶 的仰角为40°.求嵩岳寺塔的高度.(结果精确到 .参考数据: , , , , , )
19. 如图,在 中, ,点 是 的中点.以 为直径的 交 于点 ,连接 .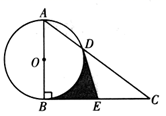 (1)、求证: 是 的切线;(2)、若 , ,求阴影部分的面积.20. 为了保障羊肉正常供应,某畜牧集团的 , 两个养殖场共出栏肥羊2000只, 养殖场的肥羊数量是 养殖场的2倍少400只.这批肥羊将运往甲地1300只,乙地700只,运费如下表(单位:元/只)
(1)、求证: 是 的切线;(2)、若 , ,求阴影部分的面积.20. 为了保障羊肉正常供应,某畜牧集团的 , 两个养殖场共出栏肥羊2000只, 养殖场的肥羊数量是 养殖场的2倍少400只.这批肥羊将运往甲地1300只,乙地700只,运费如下表(单位:元/只)养殖场
目的地
甲
25
18
乙
20
24
(1)、求 , 养殖场各出栏多少只肥羊?(2)、设这批肥羊从 养殖场运往甲地 只 ,全部运往甲、乙两地的总费用为 元,求 与 的函数关系式,并设计使总运费最少的调运方案;(3)、当每只肥羊的运费下降 元( 且 为整数)时,按(2)中设计的调运方案,总运费不超过30000元,求 的最小值.21. 如图,抛物线 与 轴交于点 和点 ,交 轴于点 ,连接 , ,已知 ,且 的面积为 .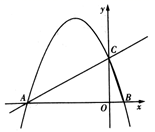 (1)、求抛物线的解析式;(2)、点 是直线 上方抛物线上一动点,过点 作 轴,交直线 于点 .抛物线上是否存在点 ,使以 , , , 为顶点的四边形是平行四边形?若存在,请求出点 的坐标;若不存在,请说明理由.22. 在 中, ,点 是 的中点, 为直线 上一动点,连接 .过点 作 ,交直线 于点 ,连接 .
(1)、求抛物线的解析式;(2)、点 是直线 上方抛物线上一动点,过点 作 轴,交直线 于点 .抛物线上是否存在点 ,使以 , , , 为顶点的四边形是平行四边形?若存在,请求出点 的坐标;若不存在,请说明理由.22. 在 中, ,点 是 的中点, 为直线 上一动点,连接 .过点 作 ,交直线 于点 ,连接 .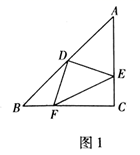
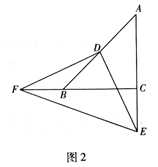
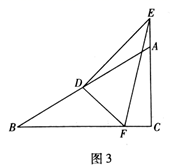 (1)、如图1,若 ,当点 在边 上, , 时, ;(2)、如图2,若 ,当点 在 的延长线上时,设 , ,求 的长(用含 , 的式子表示);(3)、如图3,若 ,当点 在 的延长线上时,用等式表示线段 , , 之间的数量关系,并证明.23. 小亮在学习中遇到如下一个问题:
(1)、如图1,若 ,当点 在边 上, , 时, ;(2)、如图2,若 ,当点 在 的延长线上时,设 , ,求 的长(用含 , 的式子表示);(3)、如图3,若 ,当点 在 的延长线上时,用等式表示线段 , , 之间的数量关系,并证明.23. 小亮在学习中遇到如下一个问题:如图1,点 是半圆 上一动点,线段 , 平分 ,过点 作 交 于点 ,连接 .当 为等腰三角形时,求线段 的长度.

小亮分析发现,此问题很难通过常规的推理计算彻底解决,于是他尝试结合学习函数的经验研究此问题.将线段 的长度作为自变量 , , 和 的长度都是 的函数,分别记为 , 和 .请将下面的探究过程补充完整:
(1)、根据点 在半圆 上的不同位置,画出相应的图形,测量线段 , , 的长度,得到下表的几组对应值:0
1.0
2.0
3.0
4.0
4.5
5.0
5.5
6
6
5.9
5.7
5.2
4.5
3.3
2.4
0
6
5.0
4.2
3.7
4
4.5
5.3
6.3
8.5
①上表中 的值是 ▲ ;
②操作中发现,“无需测量线段 的长度即可得到 关于 的函数解析式”.请直接写出 关于 的函数解析式.
(2)、小亮已在平面直角坐标系 中画出了函数 的图象,如图2所示.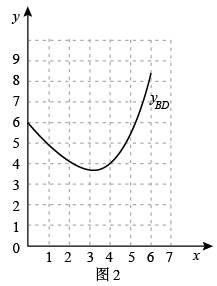
①请在同一坐标系中画出函数 和 的图象;
②结合图象直接写出当 为等腰三角形时,线段 长度的近似值(结果保留一位小数)
(3)、小亮观察发现,函数 的图象有最低点.请你直接写出线段 长度的最小值(写出精确值)