广东省茂名市新华街道三校联考2021-2022学年九年级上学期数学第一次月考试卷
试卷更新日期:2021-10-19 类型:月考试卷
一、单选题
-
1. 下列方程是一元二次方程的是( )A、2x﹣3y+1 B、3x+y=z C、x2﹣5x=1 D、x2﹣ +2=02. 下列说法正确的是( )A、矩形对角线相互垂直平分 B、对角线相等的菱形是正方形. C、两邻边相等的四边形是菱形 D、对角线分别平分对角的四边形是平行四边形3. 用配方法解一元二次方程 ,配方正确的是( )A、 B、 C、 D、4. 如图,AC,BD是菱形ABCD的对角线,BH垂直AD于点H,若AC=4,BD=3,则BH的长为( )
 A、2.4 B、2.5 C、4.8 D、55. 在一个不透明的袋子里装有红球,黄球共60个,这些球除颜色外其他都相同.小明通过多次试验发现,摸出红球的频率稳定在0.25左右,则袋子中红球的个数最有可能是( )A、9 B、15 C、18 D、246. 如图,在菱形ABCD中,对角线AC , BD相交于点O , AC=8,BD=6,点E , F分别为AO , DO的中点,则线段EF的长为( )
A、2.4 B、2.5 C、4.8 D、55. 在一个不透明的袋子里装有红球,黄球共60个,这些球除颜色外其他都相同.小明通过多次试验发现,摸出红球的频率稳定在0.25左右,则袋子中红球的个数最有可能是( )A、9 B、15 C、18 D、246. 如图,在菱形ABCD中,对角线AC , BD相交于点O , AC=8,BD=6,点E , F分别为AO , DO的中点,则线段EF的长为( )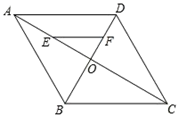 A、2.5 B、3 C、4 D、57. 菱形ABCD的一条对角线长为6cm,边AB的长是方程x2﹣7x+12=0的一个根,则菱形ABCD的周长等于( )A、10cm B、12 cm C、16cm D、12cm或16cm8. 某广场绿化工程中有一块长2千米,宽1千米的矩形空地,计划在其中修建两块相同的矩形绿地,两块绿地之间及周边留有宽度相等的人行通道(如图),并在这些人行通道铺上瓷砖,要求铺瓷砖的面积是矩形空地面积的 ,设人行通道的宽度为x千米,则下列方程正确的是( )
A、2.5 B、3 C、4 D、57. 菱形ABCD的一条对角线长为6cm,边AB的长是方程x2﹣7x+12=0的一个根,则菱形ABCD的周长等于( )A、10cm B、12 cm C、16cm D、12cm或16cm8. 某广场绿化工程中有一块长2千米,宽1千米的矩形空地,计划在其中修建两块相同的矩形绿地,两块绿地之间及周边留有宽度相等的人行通道(如图),并在这些人行通道铺上瓷砖,要求铺瓷砖的面积是矩形空地面积的 ,设人行通道的宽度为x千米,则下列方程正确的是( ) A、(2-3x)(1-2x)=1 B、 (2-3x)(1-2x)=1 C、 (2-3x)(1-2x)=1 D、 (2-3x)(1-2x)=29. 如图,将矩形ABCD绕点A旋转至矩形AEFG的位置,此时点D恰好与AF的中点重合,AE交CD于点H,若BC=2 ,则HC的长为( )
A、(2-3x)(1-2x)=1 B、 (2-3x)(1-2x)=1 C、 (2-3x)(1-2x)=1 D、 (2-3x)(1-2x)=29. 如图,将矩形ABCD绕点A旋转至矩形AEFG的位置,此时点D恰好与AF的中点重合,AE交CD于点H,若BC=2 ,则HC的长为( )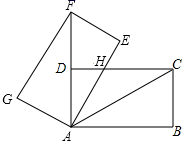 A、4 B、2 C、3 D、610. 如图, , ,点A在 上,四边形 是矩形,连接 、 交于点E,连接 交 于点F.下列4个判断:① 平分 ;② ;③ ;④若点G是线段 的中点,则 为等腰直角三角形.正确判断的个数是( )
A、4 B、2 C、3 D、610. 如图, , ,点A在 上,四边形 是矩形,连接 、 交于点E,连接 交 于点F.下列4个判断:① 平分 ;② ;③ ;④若点G是线段 的中点,则 为等腰直角三角形.正确判断的个数是( ) A、4 B、3 C、2 D、1
A、4 B、3 C、2 D、1二、填空题
-
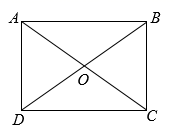
11. 若关于x的一元二次方程(m-1)x2+5x+m2-1=0的一个根是0,则m的值是 .12. 如图,矩形ABCD的对角线AC , BD相交于点O , 若AB=8,BC=6,则OD的长为 .
 13. 不透明袋子中装有黑球1个、白球2个,这些球除了颜色外无其他差别.从袋子中随机摸出一个球,记下颜色后放回,将袋子中的球摇匀,再随机摸出一个球,记下颜色,前后两次摸出的球都是白球的概率是.14. 已知关于x的一元二次方程(m-2)2x2+(2m+1)x+1=0有两个实数根,则m的取值范围是.15. 如图,将菱形ABCD折叠,使点B落在AD边的点F处,折痕为CE . 若∠D=70°,则∠AEF= .
13. 不透明袋子中装有黑球1个、白球2个,这些球除了颜色外无其他差别.从袋子中随机摸出一个球,记下颜色后放回,将袋子中的球摇匀,再随机摸出一个球,记下颜色,前后两次摸出的球都是白球的概率是.14. 已知关于x的一元二次方程(m-2)2x2+(2m+1)x+1=0有两个实数根,则m的取值范围是.15. 如图,将菱形ABCD折叠,使点B落在AD边的点F处,折痕为CE . 若∠D=70°,则∠AEF= .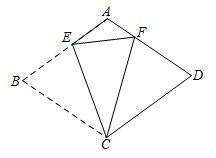 16. 已知a,b是一元二次方程x2﹣2x﹣2020=0的两个根,则a2+2b﹣3的值等于.17. 如图,在边长为10的菱形ABCD中,对角线BD=16,点O是线段BD上的动点,OE⊥AB于E , OF⊥AD于F . 则OE+OF= .
16. 已知a,b是一元二次方程x2﹣2x﹣2020=0的两个根,则a2+2b﹣3的值等于.17. 如图,在边长为10的菱形ABCD中,对角线BD=16,点O是线段BD上的动点,OE⊥AB于E , OF⊥AD于F . 则OE+OF= .
三、解答题
-
18. 解方程(1)、x2 –9 = 0(2)、x2+4x -1= 019. 如图,矩形ABCD的对角线AC、BD相交于点O,BE∥AC,CE∥DB.
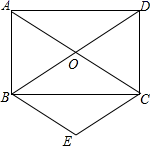 (1)、求证:四边形OBEC是菱形;(2)、若AD=4,AB=2,求菱形OBEC的面积.20. 如图,有长为30m的篱笆,一面利用墙(墙的最大可用长度为10m),围成中间隔有一道篱笆(平行于AB)的长方形花圃.
(1)、求证:四边形OBEC是菱形;(2)、若AD=4,AB=2,求菱形OBEC的面积.20. 如图,有长为30m的篱笆,一面利用墙(墙的最大可用长度为10m),围成中间隔有一道篱笆(平行于AB)的长方形花圃. (1)、设花圃的一边AB为xm,则BC的长可用含x的代数式表示为m;(2)、当AB的长是多少米时,围成的花圃面积为63平方米?21. 已知关于 的方程 .(1)、求证:无论 取何实数,此方程都有两个不相等的实数根;(2)、若方程的两根互为相反数,求 的值.22. 某数学小组为调查重庆实验外国语学校周五放学时学生的回家方式,随机抽取了部分学生进行调查,所有被调查的学生都需从“ :乘坐电动车, :乘坐普通公交车或地铁, :乘坐学校的定制公交车, :乘坐家庭汽车, :步行或其他”这五种方式中选择最常用的一种,随后该数学小组将所有调查结果整理后绘制成如图不完整的条形统计图和扇形统计图,请结合统计图回答下列问题.
(1)、设花圃的一边AB为xm,则BC的长可用含x的代数式表示为m;(2)、当AB的长是多少米时,围成的花圃面积为63平方米?21. 已知关于 的方程 .(1)、求证:无论 取何实数,此方程都有两个不相等的实数根;(2)、若方程的两根互为相反数,求 的值.22. 某数学小组为调查重庆实验外国语学校周五放学时学生的回家方式,随机抽取了部分学生进行调查,所有被调查的学生都需从“ :乘坐电动车, :乘坐普通公交车或地铁, :乘坐学校的定制公交车, :乘坐家庭汽车, :步行或其他”这五种方式中选择最常用的一种,随后该数学小组将所有调查结果整理后绘制成如图不完整的条形统计图和扇形统计图,请结合统计图回答下列问题. (1)、本次调查中一共调查了名学生;扇形统计图中, 选项对应的扇形圆心角是度;(2)、请补全条形统计图;(3)、若甲、乙两名学生放学时从 、 、 三种方式中随机选择一种,请用列表法或画树状图的方法,求出甲、乙两名学生恰好选择同一种交通工具上班的概率.23. 某商场销售一批衬衫,平均每天可以售出20件,每件盈利40元。为回馈顾客,商场决定采取适当的降价措施。经调查发现,每件衬衫降价1元,商场平均每天可多售出2件。(1)、若每件衬衫降价5元,商场可售出多少件?(2)、若商场每天的盈利要达到1200元,每件衬衫应降价多少元?24. 如图,在平面直角坐标系中,点O是坐标原点,四边形ABCO是菱形,点A的坐标为(﹣3,4),点C在x轴的正半轴上,直线AC交y轴于点M , AB边交y轴于点H , 连接BM .
(1)、本次调查中一共调查了名学生;扇形统计图中, 选项对应的扇形圆心角是度;(2)、请补全条形统计图;(3)、若甲、乙两名学生放学时从 、 、 三种方式中随机选择一种,请用列表法或画树状图的方法,求出甲、乙两名学生恰好选择同一种交通工具上班的概率.23. 某商场销售一批衬衫,平均每天可以售出20件,每件盈利40元。为回馈顾客,商场决定采取适当的降价措施。经调查发现,每件衬衫降价1元,商场平均每天可多售出2件。(1)、若每件衬衫降价5元,商场可售出多少件?(2)、若商场每天的盈利要达到1200元,每件衬衫应降价多少元?24. 如图,在平面直角坐标系中,点O是坐标原点,四边形ABCO是菱形,点A的坐标为(﹣3,4),点C在x轴的正半轴上,直线AC交y轴于点M , AB边交y轴于点H , 连接BM . (1)、菱形ABCO的边长;(2)、求直线AC的解析式;(3)、动点P从点A出发,沿折线ABC以1个单位/秒的速度向终点C匀速运动,设△PMB的面积为S , 点P的运动时间为t秒,
(1)、菱形ABCO的边长;(2)、求直线AC的解析式;(3)、动点P从点A出发,沿折线ABC以1个单位/秒的速度向终点C匀速运动,设△PMB的面积为S , 点P的运动时间为t秒,①求S与t之间的函数关系式;
②在点P运动过程中,当S=3时,请直接写出t的值.
25. 在 中,直线 经过点 , 于 , 于 , 于 .请解答下列问题:

 (1)、如图①,求证: ;(提示:过点 作 于 )(2)、如图②、图③,线段 , , 之间又有怎样的数量关系?请写出你的猜想,不需要证明;(3)、在(1)(2)的条件下,若 , , ,则 .
(1)、如图①,求证: ;(提示:过点 作 于 )(2)、如图②、图③,线段 , , 之间又有怎样的数量关系?请写出你的猜想,不需要证明;(3)、在(1)(2)的条件下,若 , , ,则 .