福建省厦门市海沧区2021年初中毕业班诊断性练习数学试卷(一模)
试卷更新日期:2021-10-19 类型:中考模拟
一、单选题
-
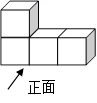
1. -2021的绝对值等于( )A、2021 B、-2021 C、 D、2. 如图,是由4个大小相同的正方体组合而成的几何体,其左视图是( )
 A、
A、 B、
B、 C、
C、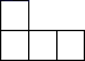 D、
D、 3. 已知点A与点B关于原点对称,若点A的坐标为(-2,3),则点B的坐标( )A、(-3,2) B、(2,-3) C、(3,2) D、(-2,-3)4. 下列运算错误的是( )A、a+2a=3a B、 C、 D、5. 某校举办“喜迎建党100周年”校园朗诵大赛,小丽同学根据比赛中七位评委所给的某位参赛选手的分数,制作了一个表格,如果去掉一个最高分和一个最低分,则表中数据一定不发生变化的是( )
3. 已知点A与点B关于原点对称,若点A的坐标为(-2,3),则点B的坐标( )A、(-3,2) B、(2,-3) C、(3,2) D、(-2,-3)4. 下列运算错误的是( )A、a+2a=3a B、 C、 D、5. 某校举办“喜迎建党100周年”校园朗诵大赛,小丽同学根据比赛中七位评委所给的某位参赛选手的分数,制作了一个表格,如果去掉一个最高分和一个最低分,则表中数据一定不发生变化的是( )中位数
众数
平均数
方差
9.3
9.4
9.2
9.5
A、中位数 B、众数 C、平均数 D、方差6. 已知关于x的一元二次方程 有一个根为 ,则a的值为( )A、0 B、±1 C、1 D、-17. 如图所示,在4×4的网格中,A、B、C、D、O均在格点上,则点O是( )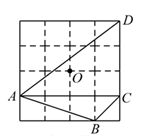 A、△ABC的内心 B、△ABC的外心 C、△ACD的外心 D、△ACD的重心8. 如图,四边形ABCD内接于⊙O,已知∠BAD=∠BCD=90°,AD=CD,且∠ADC=120,若点E为弧BC的中点,连接DE,则∠CDE的大小是( )
A、△ABC的内心 B、△ABC的外心 C、△ACD的外心 D、△ACD的重心8. 如图,四边形ABCD内接于⊙O,已知∠BAD=∠BCD=90°,AD=CD,且∠ADC=120,若点E为弧BC的中点,连接DE,则∠CDE的大小是( )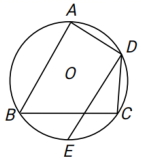 A、25° B、30° C、35° D、40°9. 如图,在正五边形 中,连接 ,以点 为圆心, 为半径画弧交 于点 ,连接 ,则 的度数是( )
A、25° B、30° C、35° D、40°9. 如图,在正五边形 中,连接 ,以点 为圆心, 为半径画弧交 于点 ,连接 ,则 的度数是( ) A、 B、 C、 D、10. 抛物线 (其中b,c是常数)过点A(2,6),且抛物线的对称轴与线段 ( )有交点,则c的值不可能是( )A、5 B、7 C、10 D、14
A、 B、 C、 D、10. 抛物线 (其中b,c是常数)过点A(2,6),且抛物线的对称轴与线段 ( )有交点,则c的值不可能是( )A、5 B、7 C、10 D、14二、填空题
-
11. sin45°=12. 如图,AB CD,BE交AD于点E,若 , ,则∠BED的度数为
 13. 某批篮球的质量检验结果如下:
13. 某批篮球的质量检验结果如下:抽取的篮球数
100
200
400
600
800
1000
1200
优等品的频数
93
192
380
561
752
941
1128
优等品的频率
从这批篮球中,任意抽取一只篮球是优等品的概率的估计值是.(精确到 )
14. 在△ABC中,以下命题正确的有①如果AD⊥BC,点D为BC中点,那么直线AD是BC的垂直平分线;②如果AD⊥BC, ,那么直线AD是BC的垂直平分线;③如果AD⊥BC, ,那么直线AD是BC的垂直平分线;④如果AD⊥BC,AB=AC,那么直线AD是BC的垂直平分线
15. 我国古代数学名著《九章算术》中“开立圆术”曰:置积尺数,以十六乘之,九而一,所得开立方除之,即立圆径,“开立圆术”相当于给出了已知球的体积V,求其直径d的一个近似公式 .我们知道球的体积公式为 ,那么利用开立圆术求直径相当于体积公式中的p=16. 如图,Rt△AOB的顶点O是坐标原点,点B在x轴上,∠OAB=90°,反比例函数 ( )的图象关于AO所在的直线对称,且与AO、AB分别交于D、E两点,过点A作AH⊥OB交x轴于点H,过点E作EF OB交AH于点G,交AO于点F,则四边形OHGF的面积为
三、解答题
-
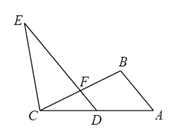
17. 解方程18. 如图,点D、F分别为AC、BC的中点, , ,求证:
 19. 先化简,再求值: ,其中x= .20. 为落实“精准扶贫”精神,市农科院专家指导贫困户李大爷种植优质百香果喜获丰收,上市20天全部销售完,专家对销售情况进行了跟踪记录,并将记录情况绘成图象,日销售量y(单位:千克)与上市时间x(单位:天)的函数关系如图所示.
19. 先化简,再求值: ,其中x= .20. 为落实“精准扶贫”精神,市农科院专家指导贫困户李大爷种植优质百香果喜获丰收,上市20天全部销售完,专家对销售情况进行了跟踪记录,并将记录情况绘成图象,日销售量y(单位:千克)与上市时间x(单位:天)的函数关系如图所示.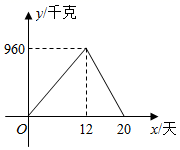 (1)、观察图示,直接写出日销售量的最大值为;(2)、根据图示,求李大爷家百香果的日销售量y与上市时间x的函数解析式,并求出第15天的日销售量.21. 如图, , ∠BAD
(1)、观察图示,直接写出日销售量的最大值为;(2)、根据图示,求李大爷家百香果的日销售量y与上市时间x的函数解析式,并求出第15天的日销售量.21. 如图, , ∠BAD (1)、在AC上方求作求作一点E,使得△ACE∽△ABD(要求:尺规作图,保留作图痕迹,不写作法)(2)、在(1)的条件下,连接DE,若 , ,求证:22. 从某城市的行政中心到市图书馆上班,有以下两种出行方式:方式一:乘坐地铁二号线到换乘点A站,换乘地铁一号线至B站下车,再步行3分钟;方式二:乘坐地铁二号线到换乘点A站,出站后打车至市图书馆,出站需2分钟时间(1)、从二号线换乘点到一号线需要步行一段距离.小明随机记录了200名乘客换乘需要的步行时间如图.如果这些乘客中有一位10:45到达二号线A站,地铁一号线10:48到达A站,停留30秒(含开关门时间);那么该乘客能赶上该趟一号线的概率是多少?
(1)、在AC上方求作求作一点E,使得△ACE∽△ABD(要求:尺规作图,保留作图痕迹,不写作法)(2)、在(1)的条件下,连接DE,若 , ,求证:22. 从某城市的行政中心到市图书馆上班,有以下两种出行方式:方式一:乘坐地铁二号线到换乘点A站,换乘地铁一号线至B站下车,再步行3分钟;方式二:乘坐地铁二号线到换乘点A站,出站后打车至市图书馆,出站需2分钟时间(1)、从二号线换乘点到一号线需要步行一段距离.小明随机记录了200名乘客换乘需要的步行时间如图.如果这些乘客中有一位10:45到达二号线A站,地铁一号线10:48到达A站,停留30秒(含开关门时间);那么该乘客能赶上该趟一号线的概率是多少? (2)、从到达二号线换乘点A站至出一号线B站需15分钟,若从A站出站,直接打车到市图书馆大概需要12~20分钟;小海对他两个月40个工作日打车的时间做了统计如下表,请你运用所学的统计知识判断这两个月选择哪种上班方式更省时间
(2)、从到达二号线换乘点A站至出一号线B站需15分钟,若从A站出站,直接打车到市图书馆大概需要12~20分钟;小海对他两个月40个工作日打车的时间做了统计如下表,请你运用所学的统计知识判断这两个月选择哪种上班方式更省时间行程时间x/分钟
次数
12≤x<14
6
14≤x<16
10
16≤x<18
m
18≤x<20
9
23. 如图,点D为△ABC外接圆上一点,∠ABC=90°,BD与AC交于点E,点F在BD延长线上,∠DAF=∠ABD (1)、求证:AF与△ABC的外接圆相切(2)、若点D为EF的中点, , ,求EF的长24. 在矩形ABCD中,点E是线段BC上一动点,连接AE,过点B作BF⊥AE于点G,交直线CD于点F
(1)、求证:AF与△ABC的外接圆相切(2)、若点D为EF的中点, , ,求EF的长24. 在矩形ABCD中,点E是线段BC上一动点,连接AE,过点B作BF⊥AE于点G,交直线CD于点F
 (1)、如图1,当矩形ABCD是正方形时,以点F为直角顶点在正方形ABCD的外部作等腰 ,连接EH.判断线段AE与EH之间的关系,并说明理由;(2)、如图2,以BE和BF为邻边作▱BEHF,M是BH中点,连接GM,AB=5,BC=4,求GM的最小值25. 已知抛物线 (a≠0)与y轴交于点C,与x轴交于点A和B(点A在点B左侧),若△ABC是等腰三角形,则称抛物线 (a≠0)是“理想抛物线”,(1)、判断抛物线 是否为“理想抛物线”,并说明理由;(2)、已知经过点B(3,0)的抛物线 ( )是“理想抛物线”;
(1)、如图1,当矩形ABCD是正方形时,以点F为直角顶点在正方形ABCD的外部作等腰 ,连接EH.判断线段AE与EH之间的关系,并说明理由;(2)、如图2,以BE和BF为邻边作▱BEHF,M是BH中点,连接GM,AB=5,BC=4,求GM的最小值25. 已知抛物线 (a≠0)与y轴交于点C,与x轴交于点A和B(点A在点B左侧),若△ABC是等腰三角形,则称抛物线 (a≠0)是“理想抛物线”,(1)、判断抛物线 是否为“理想抛物线”,并说明理由;(2)、已知经过点B(3,0)的抛物线 ( )是“理想抛物线”;①若点P( ),Q( )( )是抛物线上另两点,满足当 时,PB与AQ的交点始终在抛物线的对称轴上,且线段AC的垂直平分线恰好经过点B,求此抛物线的解析式;
②是否存在整数c使得 ,且 ,若存在,求出所有满足条件的整数c的值;若不存在,请说明理由.