广东省茂名市东山街道三校联考2021-2022学年九年级上学期数学第一次月考试卷
试卷更新日期:2021-10-19 类型:月考试卷
一、单选题
-
1. 下列命题中,是真命题的是( )A、对角线相等的四边形是平行四边形 B、对角线互相垂直的平行四边形是矩形 C、菱形的对角线相等 D、有一组邻边相等的平行四边形是菱形2. 用配方法解一元二次方程 时,下列变形正确的是( ).A、 B、 C、 D、3. 如图,在矩形 中,点 在 上,点 在 上,把这个矩形沿 折叠后,使点 恰好落在点 处,若 , ,则折痕 的长为( )
 A、1 B、 C、2 D、4. 已知一元二次方程x2﹣10x+24=0的两个根是菱形的两条对角线长,则这个菱形的面积为( )A、6 B、10 C、12 D、245. 某模具公司销售员小王一月份销售额为8万元,已知小王第一季度销售额为34.88万元,若设小王平均每月销售额的增长率均为 ,可以列出方程为( )A、 B、 C、 D、6. 如图,菱形ABCD中,AC交BD于点O, 于点E,连接OE,若 ,则 ( )
A、1 B、 C、2 D、4. 已知一元二次方程x2﹣10x+24=0的两个根是菱形的两条对角线长,则这个菱形的面积为( )A、6 B、10 C、12 D、245. 某模具公司销售员小王一月份销售额为8万元,已知小王第一季度销售额为34.88万元,若设小王平均每月销售额的增长率均为 ,可以列出方程为( )A、 B、 C、 D、6. 如图,菱形ABCD中,AC交BD于点O, 于点E,连接OE,若 ,则 ( ) A、20° B、30° C、40° D、50°7. 在解一元二次方程x2+px+q=0时,小红看错了常数项q,得到方程的两个根是﹣3,1.小明看错了一次项系数P,得到方程的两个根是5,﹣4,则原来的方程是( )A、x2+2x﹣3=0 B、x2+2x﹣20=0 C、x2﹣2x﹣20=0 D、x2﹣2x﹣3=08. 如图,在 中,M,N是 上两点, ,连接 , , , ,添加一个条件,使四边形 是菱形,这个条件是( )
A、20° B、30° C、40° D、50°7. 在解一元二次方程x2+px+q=0时,小红看错了常数项q,得到方程的两个根是﹣3,1.小明看错了一次项系数P,得到方程的两个根是5,﹣4,则原来的方程是( )A、x2+2x﹣3=0 B、x2+2x﹣20=0 C、x2﹣2x﹣20=0 D、x2﹣2x﹣3=08. 如图,在 中,M,N是 上两点, ,连接 , , , ,添加一个条件,使四边形 是菱形,这个条件是( )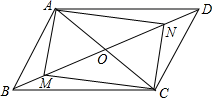 A、 B、 C、 D、9. 如图,在菱形 中, , , 于点 ,则 的长为( )
A、 B、 C、 D、9. 如图,在菱形 中, , , 于点 ,则 的长为( )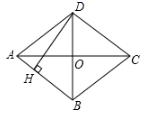 A、3 B、 C、2 D、10. 如图,正方形 中,在 的延长线上取点 , ,使 , ,连接 分别交 , 于 , ,下列结论:① ;② ;③图中有8个等腰三角形;④ .其中正确的结论个数是( )
A、3 B、 C、2 D、10. 如图,正方形 中,在 的延长线上取点 , ,使 , ,连接 分别交 , 于 , ,下列结论:① ;② ;③图中有8个等腰三角形;④ .其中正确的结论个数是( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 如图,BD是菱形ABCD的一条对角线,点E在BC的延长线上,若 ,则 的度数为度.
 12. 若关于 的一元二次方程 有两个不相等的实数根,则 的取值范围是.13. 一个暗箱中放有除颜色外其他完全相同的m个红球,6个黄球,3个白球.现将球搅匀后,任意摸出1个球记下颜色,再放回暗箱,通过大量重复试验后发现,摸到黄球的频率稳定在30%附近,由此可以估算m的值是 .14. 已知a、b是一元二次方程x2+x-2021=0的两个不相等的实数根,则a2+2a+b的值为.15. 有长为30m的篱笆,如图所示,一面靠墙(墙足够长),围成中间隔有一道篱笆的长方形花圃,当花圃的面积是72m2时,则AB= .
12. 若关于 的一元二次方程 有两个不相等的实数根,则 的取值范围是.13. 一个暗箱中放有除颜色外其他完全相同的m个红球,6个黄球,3个白球.现将球搅匀后,任意摸出1个球记下颜色,再放回暗箱,通过大量重复试验后发现,摸到黄球的频率稳定在30%附近,由此可以估算m的值是 .14. 已知a、b是一元二次方程x2+x-2021=0的两个不相等的实数根,则a2+2a+b的值为.15. 有长为30m的篱笆,如图所示,一面靠墙(墙足够长),围成中间隔有一道篱笆的长方形花圃,当花圃的面积是72m2时,则AB= . 16. 如图,正方形纸片 的边长为4,点 在边 上,连接 ,将纸片沿着直线 翻折,点 的对应点为点 ,连接 并延长交 于点 ,若 ,则 .
16. 如图,正方形纸片 的边长为4,点 在边 上,连接 ,将纸片沿着直线 翻折,点 的对应点为点 ,连接 并延长交 于点 ,若 ,则 . 17. 如图,正方形OABC的边长为2,将正方形OABC绕点O逆时针旋转角α(0°<α<180°)得到正方形OA′B′C′,连接BC′,当点A′恰好落在线段BC′上时,线段BC′的长度是 .
17. 如图,正方形OABC的边长为2,将正方形OABC绕点O逆时针旋转角α(0°<α<180°)得到正方形OA′B′C′,连接BC′,当点A′恰好落在线段BC′上时,线段BC′的长度是 .
三、解答题
-
18. 解下列方程:(1)、 ;(2)、 .19. 为了迎接建党100周年,学校举办了“感党恩•跟党走”主题社团活动,小颖喜欢的社团有写作社团、书画社团、演讲社团、舞蹈社团(分别用字母A , B , C , D依次表示这四个社团),并把这四个字母分别写在四张完全相同的不透明的卡片正面,然后将这四张卡片背面朝上洗匀后放在桌面上.(1)、小颖从中随机抽取一张卡片是舞蹈社团D的概率是;(2)、小颖先从中随机抽取一张卡片,记录下卡片上的字母不放回,再从剩下的卡片中随机抽取一张卡片,记录下卡片上的字母,请用列表法或画树状图法求出小颖抽取的两张卡片中有一张是演讲社团C的概率.20. 如图,在矩形ABCD中,点O为对角线AC的中点,过点O作 交BC于点E,交AD于点F,连接AE,CF.
 (1)、求证:四边形AECF是菱形;(2)、连接OB,若 , ,求OB的长.21. 已知关于 的一元二次方程 ,其中 、 、 分别为 三边的长.(1)、如果 是方程的根,试判断 的形状,并说明理由;(2)、如果 是等边三角形,试求这个一元二次方程的根.22. 2021年是中国共产党建党100周年华诞.“五一”后某校组织了八年级学生参加建党100周年知识竞赛,为了了解学生对党史知识的掌握情况,学校随机抽取了部分同学的成绩作为样本,把成绩按不及格、合格、良好、优秀四个等级分别进行统计,并绘制了如下不完整的条形统计图与扇形统计图:
(1)、求证:四边形AECF是菱形;(2)、连接OB,若 , ,求OB的长.21. 已知关于 的一元二次方程 ,其中 、 、 分别为 三边的长.(1)、如果 是方程的根,试判断 的形状,并说明理由;(2)、如果 是等边三角形,试求这个一元二次方程的根.22. 2021年是中国共产党建党100周年华诞.“五一”后某校组织了八年级学生参加建党100周年知识竞赛,为了了解学生对党史知识的掌握情况,学校随机抽取了部分同学的成绩作为样本,把成绩按不及格、合格、良好、优秀四个等级分别进行统计,并绘制了如下不完整的条形统计图与扇形统计图: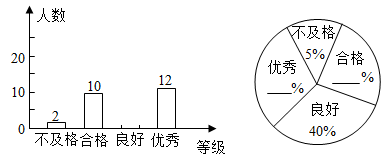
请根据图中提供的信息解答下列问题:
(1)、根据给出的信息,将这两个统计图补充完整(不必写出计算过程);(2)、该校八年级有学生650人,请估计成绩未达到“良好”及以上的有多少人?(3)、“优秀”学生中有甲、乙、丙、丁四位同学表现突出,现从中派2人参加区级比赛,求抽到甲、乙两人的概率.23. 超市销售某种儿童玩具,经市场调查发现,每件利润为 元时,每天可售出 件;销售单价每增加 元,每天销售量会减少 件.物价管理部门规定,该种玩具每件利润不得超过 元.设销售单价增加 元,每天可售出 件.(1)、写出 与 之间的函数关系式(不要求写出自变量取值范围);(2)、当 取何值时,超市每天销售这种玩具可获得利润 元?此时每天可销售多少件?24. 如图, 中,∠ACB=90°,AC=6cm,BC=8cm,点P从点A出发,以每秒1cm的速度沿AC运动;同时点Q从点C出发,以每秒2cm的速度沿CB运动,当Q到达点B时,点P同时停止运动. (1)、运动几秒时 的面积为5cm2?(2)、运动几秒时 中PQ=6 cm?(3)、 的面积能否等于10cm2?若能,求出运动时间,若不能,说明理由.25. 如图①,在矩形 中,点A在 轴正半轴上,点 在 轴正半轴上,点 在第一象限, , .
(1)、运动几秒时 的面积为5cm2?(2)、运动几秒时 中PQ=6 cm?(3)、 的面积能否等于10cm2?若能,求出运动时间,若不能,说明理由.25. 如图①,在矩形 中,点A在 轴正半轴上,点 在 轴正半轴上,点 在第一象限, , . (1)、直接写出点 的坐标:;(2)、如图②,点 在 边上,连接 ,将 沿 折叠,点 恰好与线段 上一点 重合,求线段 的长度;(3)、如图③, 是直线 上一点, 交线段 于 .若 在第一象限,且 ,试求符合条件的所有点 的坐标.
(1)、直接写出点 的坐标:;(2)、如图②,点 在 边上,连接 ,将 沿 折叠,点 恰好与线段 上一点 重合,求线段 的长度;(3)、如图③, 是直线 上一点, 交线段 于 .若 在第一象限,且 ,试求符合条件的所有点 的坐标.