福建省2021年中考数学精准模拟试卷
试卷更新日期:2021-10-19 类型:中考模拟
一、单选题
-
1. 的计算结果是( ).A、-3 B、-2 C、3 D、42. 月球距离地球的距离约为 ,将384000用科学记数法表示为( )A、 B、 C、 D、3. 下列几何体中,俯视图为三角形的是( )A、
 B、
B、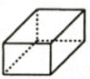 C、
C、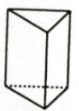 D、
D、 4. 以下调查中,适宜全面调查的是( )A、调查某批次汽车的抗撞击能力 B、调查某班学生的身高情况 C、调查春节联欢晚会的收视率 D、调查济宁市居民日平均用水量5. 下列选项中的图形,不属于中心对称图形的是( )A、等边三角形 B、正方形 C、正六边形 D、圆6. 下列运算中正确的是( )A、 B、 C、 D、7. 一个多边形的内角和是720°,这个多边形是( )A、五边形 B、六边形 C、七边形 D、八边形8. 实数 , , 在数轴上的对应点的位置如图所示,若 ,则下列结论中正确的是( )
4. 以下调查中,适宜全面调查的是( )A、调查某批次汽车的抗撞击能力 B、调查某班学生的身高情况 C、调查春节联欢晚会的收视率 D、调查济宁市居民日平均用水量5. 下列选项中的图形,不属于中心对称图形的是( )A、等边三角形 B、正方形 C、正六边形 D、圆6. 下列运算中正确的是( )A、 B、 C、 D、7. 一个多边形的内角和是720°,这个多边形是( )A、五边形 B、六边形 C、七边形 D、八边形8. 实数 , , 在数轴上的对应点的位置如图所示,若 ,则下列结论中正确的是( )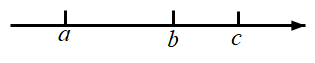 A、 B、 C、 D、9. 《九章算术》中记载了这样一个数学问题:今有甲发长安,五日至齐;乙发齐,七日至长安.今乙发已先二日,甲乃发长安.问几何日相逢?译文:甲从长安出发,5日到齐国;乙从齐国出发,7日到长安.现乙先出发2日,甲才从长安出发.问甲出发几日,甲乙相逢?设甲出发x日,甲乙相逢,可列方程( )A、 B、 C、 D、10. 已知二次函数 ,当 时,该函数取得最大值4.设该函数图象与 轴的一个交点的横坐标为 ,若 ,则 的取值范围是( )A、 B、 C、 D、
A、 B、 C、 D、9. 《九章算术》中记载了这样一个数学问题:今有甲发长安,五日至齐;乙发齐,七日至长安.今乙发已先二日,甲乃发长安.问几何日相逢?译文:甲从长安出发,5日到齐国;乙从齐国出发,7日到长安.现乙先出发2日,甲才从长安出发.问甲出发几日,甲乙相逢?设甲出发x日,甲乙相逢,可列方程( )A、 B、 C、 D、10. 已知二次函数 ,当 时,该函数取得最大值4.设该函数图象与 轴的一个交点的横坐标为 ,若 ,则 的取值范围是( )A、 B、 C、 D、二、填空题
-
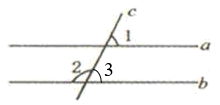
11. 如图,直线a、b被直线c所截,a∥b,∠1=70°,则∠2=.
 12. 分解因式: =.13. 某校男子篮球队10名队员进行定点投篮练习,每人投篮10次,他们投中的次数统计如表:
12. 分解因式: =.13. 某校男子篮球队10名队员进行定点投篮练习,每人投篮10次,他们投中的次数统计如表:投中次数
3
5
6
7
8
人数
1
3
2
2
2
则这些队员投中次数的众数为 .
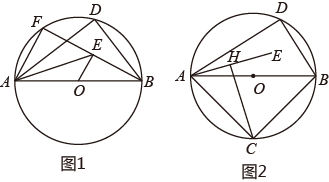
14. 如图, , ,以点 为圆心, 为半径作弧交 于点 ,点 ,交 于点 ,若 ,则阴影部分的面积为.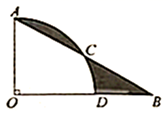 15. 如图,四边形ABCD是正方形,点E , F 分别在边 , BC 上,且CE=DF ,DE ,AF 交于点G ,AF的中点为点H ,连接BG ,DH ,现有以下结论:① ;② ;③ ;④ .其中正确的结论有 . (填写所有正确结论的序号)
15. 如图,四边形ABCD是正方形,点E , F 分别在边 , BC 上,且CE=DF ,DE ,AF 交于点G ,AF的中点为点H ,连接BG ,DH ,现有以下结论:① ;② ;③ ;④ .其中正确的结论有 . (填写所有正确结论的序号)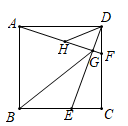 16. 在平面直角坐标系中,已知点 ,点 ,则线段 的长度的最小值是 .
16. 在平面直角坐标系中,已知点 ,点 ,则线段 的长度的最小值是 .三、解答题
-
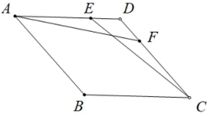
17. 解方程组:18. 如图,在菱形 中,点 、 分别在 、 上,且 .求证: .
 19. 先化简,再求值: ,其中 .20. 如图, 中, 是 边上一点.
19. 先化简,再求值: ,其中 .20. 如图, 中, 是 边上一点.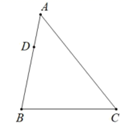 (1)、在边 上求作一点 ,使得 .(要求:尺规作图,不写作法,保留作图痕迹)(2)、在(1)的条件下,若 的面积是 面积的9倍,且 ,求 的长.21. 如图,把正方形 绕点 顺时针旋转 到正方形 , 交 于点 ,连接 , .
(1)、在边 上求作一点 ,使得 .(要求:尺规作图,不写作法,保留作图痕迹)(2)、在(1)的条件下,若 的面积是 面积的9倍,且 ,求 的长.21. 如图,把正方形 绕点 顺时针旋转 到正方形 , 交 于点 ,连接 , .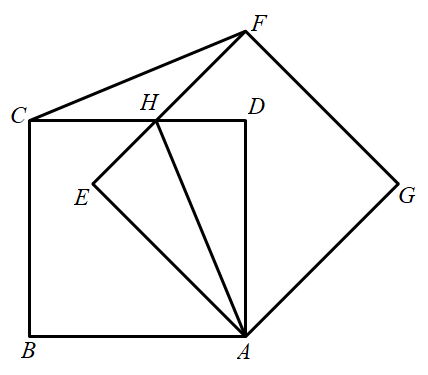
求证: .
22. 在“新冠”疫情期间,全国人民众志成城,同心抗疫,某商家决定将一个月内获得的利润全部捐赠给社区用于抗疫,已知该商家购进一批产品,成本为10元/件,拟采取线上和线下两种销售方式进行销售,调查发现,线下的月销量 (单位:件)与线下的售价 (单位:元/件, )满足函数关系式 .(1)、若线下的月销量为400件,求此时线下的售价;(2)、若线上每件的售价始终比线下便宜2元,且线上的月销量固定为400件,试问:当 为多少时,线上和线下的月利润总和达到最大?并求出此时的最大利润.23. 某印刷厂每五年需淘汰一批同款的旧打印机并购买新机.购买新机时,若同时配买墨盒,每盒150元,且最多可配买24盒;若非同时配买,则每盒需220元.根据该厂以往的记录,10台同款打印机正常工作五年消耗的墨盒数如下表:消耗的墨盒数
22
23
24
25
打印机台数
1
4
4
1
(1)、以这10台打印机五年消耗的墨盒数为样本,估计“一台该款打印机正常工作五年消耗的墨盒数不大于24”的概率;(2)、如果每台打印机购买新机时配买的墨盒只能供本机使用,试以这10台打印机消耗墨盒费用的平均数作为决策依据,说明购买 台该款打印机时,应同时配买23盒还是24盒墨?