广东省江门市开平市三校联考2021-2022学年九年级上学期数学第一次月考试卷

试卷更新日期：2021-10-19 类型：月考试卷

进入出卷网下载

一、单选题

1. 下列 $y$ 关于x的函数中，一定是二次函数的是（）

A、 $y = (k - 1) x^{2} + 3$ B、 $y = \frac{1}{x^{2}} + 1$ C、 $y = (x + 1) (x - 2) - x^{2}$ D、 $y = 2 x^{2} - 7 x$

查看试题解析
2. 将一元二次方程 $x^{2} - 2 x = 1$ 配方，其正确的结果是（）

A、 ${(x + 1)}^{2} = 2$ B、 ${(x - 2)}^{2} = 5$ C、 ${(x - 1)}^{2} = 1$ D、 ${(x - 1)}^{2} = 2$

查看试题解析
3. 已知关于x的一元二次方程 $(k - 1) x^{2} + 2 x + 1 = 0$ 没有实数解，则k的取值范围是（）

A、 $k > 2$ B、 $k < 2$ 且 $k \neq 1$ C、 $k \geq 2$ D、 $k \leq 2$ 且 $k \neq 1$

查看试题解析
4. 对于二次函数y=-2(x+3) $^{2}$ 的图象，下列说法错误的是（）

A、开口向下 B、对称轴是直线x=-3 C、顶点坐标为(-3，0) D、当x<-3时，y随x的增大而减小

查看试题解析
5. 将二次函数 $y = {(x - 1)}^{2}$ 的图象向左平移1个单位长度，再向上平移2个单位后，所得图象的函数解析式是（）

A、 $y = {(x - 2)}^{2} + 2$ B、 $y = {(x - 2)}^{2} - 2$ C、 $y = x^{2} + 2$ D、 $y = x^{2} - 2$

查看试题解析
6. 关于 $x$ 一元二次方程 $(a - 1) x^{2} + x + a^{2} - 1 = 0$ 的一个根是0，则 $a$ 的值为（）

A、1或-1 B、1 C、-1 D、0

查看试题解析
7. 若方程ax²+bx+c＝0（a＞0）的两个根是﹣3和1，则对于二次函数y＝ax²+bx+c ，当y＞0时，x的取值范围是（）

A、﹣3＜x＜1 B、x＜﹣3或x＞1 C、x＞﹣3 D、x＜1

查看试题解析
8. 将4个数 $a$ 、 $b$ 、 $c$ 、 $d$ 排成2行、2列，两边各加一条竖直线记成 $| \begin{array}{l} a & b \\ c & d \end{array} |$ ，定义 $| \begin{array}{l} a & b \\ c & d \end{array} | = a d - b c$ .例如 $| \begin{array}{l} 8 & 9 \\ 3 & 5 \end{array} | = 8 \times 5 - 9 \times 3 = 40 - 27 = 13$ .则方程 $| \begin{array}{l} x & 1 \\ 6 x & x \end{array} | = - 9$ 的根的情况为（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、只有一个实数根

查看试题解析
9. 参加足球联赛的每两支球队之间都要进行两场比赛，共要比赛110场，设参加比赛的球队有x支，根据题意，下面列出的方程正确的是（）

A、 $\frac{1}{2}$ x（x+1）＝110 B、 $\frac{1}{2}$ x（x﹣1）＝110 C、x（x+1）＝110 D、x（x﹣1）＝110

查看试题解析
10. 抛物线 $y = a x^{2} + b x + c$ （a，b，c为常数）开口向下且过点 $A (1 ， 0)$ ， $B (m ， 0)$ （ $- 2 < m < - 1$ ），下列结论：① $2 b + c > 0$ ；② $2 a + c < 0$ ；③ $a (m + 1) - b + c > 0$ ；④若方程 $a (x - m) (x - 1) - 1 = 0$ 有两个不相等的实数根，则 $4 a c - b^{2} < 4 a$ .其中正确结论的个数是（）

A、4 B、3 C、2 D、1

查看试题解析

二、填空题

11. 方程 $x^{2} - 4 x = 0$ 的解为.

查看试题解析
12. 如果一个直角三角形的两边长是一元二次方程 $x^{2} - 7 x + 12 = 0$ 的两个根，那么这个直角三角形的斜边长为．

查看试题解析
13. 已知 $m$ 、 $n$ 是方程 $x^{2} + 2 x - 2020 = 0$ 的两个实数根，则代数式 $m^{2} + m n + 3 m + n =$ ．

查看试题解析
14. 在解一元二次方程x²+bx+c＝0时，小明看错了一次项系数b，得到的解为x₁＝2，x₂＝3；小刚看错了常数项c，得到的解为x₁＝1，x₂＝5.请你写出正确的一元二次方程.

查看试题解析
15. 二次函数 $y = {(x - 1)}^{2} - 5$ 的最小值是．

查看试题解析
16. 已知二次函数 $y = - 2 {(x - 1)}^{2} + k$ 的图象上有 $A (- \sqrt{7}, y_{1})$ ， $B (2, y_{2})$ ， $C (3, y_{3})$ 三个点.用“＜”连接 $y_{1}$ ， $y_{2}$ ， $y_{3}$ 的结果是.

查看试题解析
17. 如图，在平面直角坐标系中， $R t △ A B C$ 的直角顶点 $B$ 的坐标为 $(1 ， 0)$ ，点 $A$ 在 $x$ 轴正半轴上， $A B = 2$ ，将 $△ A B C$ 绕着点 $B$ 逆时针旋转90°，得到 $△ D B O$ ，若抛物线 $y = x^{2} + b x + c$ 经过点 $A$ ， $D$ ，则 $b - c$ 的值为．

查看试题解析

三、解答题

18. 解方程：

(1)、 $2 x^{2} - 8 = 0$

(2)、 $x^{2} - 3 x + 1 = 0$

查看试题解析
19. 如图，抛物线y=x²+bx+c与y轴交于点A（0，2），对称轴为直线x=2，求此抛物线的解析式.

查看试题解析
20. 随着人民生活水平的不断提高，我市家庭轿车的拥有量逐年增加，据统计，某小区2013年底拥有家庭轿车64辆，2015年底家庭轿车的拥有量达到100辆．若该小区2013年底到2016年底家庭轿车拥有量的年平均增长率都相同。
求：

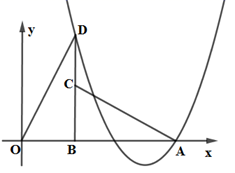
(1)、该小区2013年底到2015年底家庭轿车拥有量的年平均增长率．

(2)、该小区到2016年底家庭轿车达到多少辆？

查看试题解析
21. 已知关于x的一元二次方程 $x^{2} - 2 k x + k^{2} + k + 1 = 0$ 有两个实数根．

(1)、试求k的取值范围；

(2)、若此方程的两个实数根 $x_{1} 、 x_{2}$ ，是否存在实数k ，满足 $\frac{1}{x_{1}} + \frac{1}{x_{2}} = - 2$ ，若存在，求出k的值；若不存在，说明理由．

查看试题解析
22. 如图，抛物线 $y = - \frac{3}{4} x^{2} + b x + c$ 与 $x$ 轴交于点 $A(4，0)$ ，与 $y$ 轴交于点 $B (0 ， 3)$ ，点 $P$ 是线段 $A B$ 上方的抛物线上的动点，过点 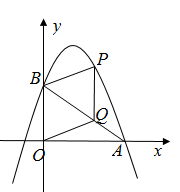$P$ 作 $P Q$ $/ /$ $y$ 轴交 $A B$ 于点 $Q$ ．

$(1)$ 求抛物线的解析式；

查看试题解析
23. 某超市销售一款“免洗洗手液”，这款“免洗洗手液”的成本价为每瓶16元，当销售单价定为20元时，每天可售出80瓶.根据市场行情，现决定降价销售.市场调查反映：销售单价每降低0.5元，则每天可多售出20瓶（销售单价不低于成本价），若设这款“免洗洗手液”的销售单价为x（元），每天的销售量为y（瓶）.

(1)、求每天的销售量y（瓶）与销售单价x（元）之间的函数关系式；

(2)、当销售单价为多少元时，销售这款“免洗洗手液”每天的销售利润最大，最大利润为多少元？

查看试题解析
24. 如图，点 $A ， B$ 在函数 $y = \frac{1}{4} x^{2}$ 的图像上．已知 $A ， B$ 的横坐标分别为－2、4，直线 $A B$ 与 $y$ 轴交于点 $C$ ，连接 $O A ， O B$ ．

(1)、求直线 $A B$ 的函数表达式；

(2)、求 $Δ A O B$ 的面积；

(3)、若函数 $y = \frac{1}{4} x^{2}$ 的图像上存在点 $P$ ，使得 $Δ P A B$ 的面积等于 $Δ A O B$ 的面积的一半，则这样的点 $P$ 共有个．

查看试题解析
25. 如图，抛物线与x轴交于 $A (- 1 ， 0) 、 B (3 ， 0)$ ，交y轴于 $C (0 ， 3)$ .

(1)、求抛物线的解析式；

(2)、P是直线 $B C$ 上方的抛物线上的一个动点，设P的横坐标为 $t ， P$ 到 $B C$ 的距离为h，求h与t的函数关系式，并求出h的最大值；

(3)、设点M是x轴上的动点，在平面直角坐标系中，存在点N，使得以点 $A 、 C 、 M 、 N$ 为顶点的四边形是菱形，直接写出所有符合条件的点N坐标.

查看试题解析