福建省2021年九年级下学期百校联考(诊断卷二)数学试卷
试卷更新日期:2021-10-19 类型:中考模拟
一、单选题
-
1. 2020的倒数是( )A、 B、 C、2020 D、-20202. 一种新型冠状病毒的直径为 ,呈球形或椭圆形,具有多形性.如果 米,那么这种新型冠状病毒的直径约为( )A、 米 B、 米 C、 米 D、 米3. 下面的图形是用数学家名字命名的,其中既是轴对称图形又是中心对称图形的是( )A、
 赵爽弦图
B、
赵爽弦图
B、 笛卡尔心形线
C、
笛卡尔心形线
C、 科克曲线
D、
科克曲线
D、 斐波那契螺旋线
4. 鲁班锁,民间也称作孔明锁,八卦锁,它起源于中国古代建筑中首创的榫卯结构.如图是鲁班锁的其中一个部件,它的左视图是( )
斐波那契螺旋线
4. 鲁班锁,民间也称作孔明锁,八卦锁,它起源于中国古代建筑中首创的榫卯结构.如图是鲁班锁的其中一个部件,它的左视图是( )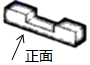 A、
A、 B、
B、 C、
C、 D、
D、 5. 一个多边形的外角和是其内角和的 倍( 为正整数),则该多边形的边数是( )A、 B、 C、 D、6. 若k为正整数,则 ( )A、 B、 C、 D、7. 在Rt ABC中,∠C=90º,下列关系式中错误的是( )A、BC=AB•sinA B、BC=AC•tanA C、AC=BC•tanB D、AC=AB•cosB8. 随着智能手机的普及,“支付宝支付”和“微信支付”等手机支付方式倍受广大消费者的青睐,某商场对2019年7−12月中使用这两种手机支付方式的情况进行统计,得到如图所示的折线图,根据统计图中的信息,得出以下四个推断,其中不合理的是( )
5. 一个多边形的外角和是其内角和的 倍( 为正整数),则该多边形的边数是( )A、 B、 C、 D、6. 若k为正整数,则 ( )A、 B、 C、 D、7. 在Rt ABC中,∠C=90º,下列关系式中错误的是( )A、BC=AB•sinA B、BC=AC•tanA C、AC=BC•tanB D、AC=AB•cosB8. 随着智能手机的普及,“支付宝支付”和“微信支付”等手机支付方式倍受广大消费者的青睐,某商场对2019年7−12月中使用这两种手机支付方式的情况进行统计,得到如图所示的折线图,根据统计图中的信息,得出以下四个推断,其中不合理的是( )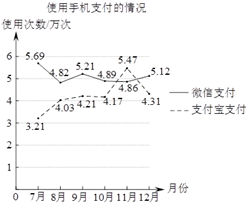 A、6个月中使用“微信支付”的总次数比使用“支付宝支付”的总次数多; B、6个月中使用“微信支付”的消费总额比使用“支付宝支付”的消费总额大; C、6个月中11月份使用手机支付的总次数最多; D、9月份平均每天使用手机支付的次数比12月份平均每天使用手机支付的次数多;9. 将等腰直角三角板ABC与量角器按如图方式放置,其中A为半圆形量角器的O刻度线,直角边BC与量角器相切于点D,斜边AB与量角器相交于点E,若量角器在点D的读数为120°,则量角器在点E的读数是( )
A、6个月中使用“微信支付”的总次数比使用“支付宝支付”的总次数多; B、6个月中使用“微信支付”的消费总额比使用“支付宝支付”的消费总额大; C、6个月中11月份使用手机支付的总次数最多; D、9月份平均每天使用手机支付的次数比12月份平均每天使用手机支付的次数多;9. 将等腰直角三角板ABC与量角器按如图方式放置,其中A为半圆形量角器的O刻度线,直角边BC与量角器相切于点D,斜边AB与量角器相交于点E,若量角器在点D的读数为120°,则量角器在点E的读数是( )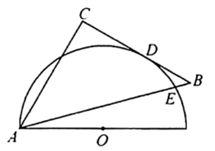 A、130° B、135° C、150° D、160°10. 已知 , , , 四个点中只有一个点不在二次函数 的图象上.下列关于这个点的说法中,正确的是( )A、这个点一定是点 B、这个点一定是点 C、这个点一定是 , 中某一点 D、这个点一定是 , 中的某一点
A、130° B、135° C、150° D、160°10. 已知 , , , 四个点中只有一个点不在二次函数 的图象上.下列关于这个点的说法中,正确的是( )A、这个点一定是点 B、这个点一定是点 C、这个点一定是 , 中某一点 D、这个点一定是 , 中的某一点二、填空题
-
11. 因式分解:4a2﹣1=.12. 我国古代数学名著《九章算术》有“米谷粒分”:粮仓开仓收粮,有人送来谷米1608石,验得其中夹有谷粒.现从中抽取谷米一把,共数得256粒,其中夹有谷粒32粒,则这批谷米内夹有谷粒约是石.13. 数轴上,点 从 点出发沿数轴向右运动4个单位长度后与点 重合,若 , 两点对应的数互为相反数,则点 表示的数为.14. 某班对学生的中考体育选考情况进行调研(每人都从以下三项中选两项),数据如下:
科目
50米跑
1分钟跳绳
立定跳远
选考人数(人)
37
15
32
则该班学生中选50米跑和立定跳远的共有人.
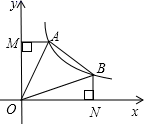
15. 如图, , ,以 为圆心, 为半径画弧交 与点 ,设图中两块阴影部分面积分别为 , ,则 .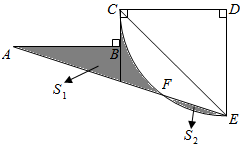 16. 如图,直线 与双曲线 交于 、 两点,连接 、 , 轴于 , 轴于 ,设 , 的解析式分别为 , ,现有以下结论:
16. 如图,直线 与双曲线 交于 、 两点,连接 、 , 轴于 , 轴于 ,设 , 的解析式分别为 , ,现有以下结论:① ;② ;③若 ,则 ;④ 有最小值.
其中正确的是.(写出所有正确结论的序号)
三、解答题
-
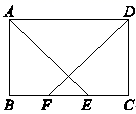
17. 解方程组18. 如图,在矩形 中, .求证: .
 19. 先化简,再求值: ,其中 .20. 疫情期间为了满足测温的需求,某学校决定购进一批额温枪.经了解市场,购买 种品牌的额温枪每支300元, 种品牌的额温枪每支350元.经与商家协商, 种品牌的额温枪降价15%, 种品牌的额温枪打八折销售.若购买两种品牌的额温枪共50支且总费用不超过13000元,则至少要购买 种品牌的额温枪多少支?21. 如图, 中, , ,点 、 分别在边 、 上,且 .
19. 先化简,再求值: ,其中 .20. 疫情期间为了满足测温的需求,某学校决定购进一批额温枪.经了解市场,购买 种品牌的额温枪每支300元, 种品牌的额温枪每支350元.经与商家协商, 种品牌的额温枪降价15%, 种品牌的额温枪打八折销售.若购买两种品牌的额温枪共50支且总费用不超过13000元,则至少要购买 种品牌的额温枪多少支?21. 如图, 中, , ,点 、 分别在边 、 上,且 .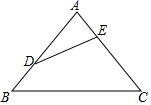 (1)、求 的度数;(2)、将 绕点 逆时针旋转100°,点 的对应点为点 ,连接 ,求证:四边形 为平行四边形.22. 越野汽车轮胎的质量是根据其正常使用的时间来衡量,使用时间越长,表明质量越好,且使用时间大于或等于7千小时的为优质品,否则为普通品.某汽修店对 , 两种不同型号的汽车轮胎做试验,各随机抽取部分产品作为样本,得到试验结果的扇形统计图和折线图如图所示.
(1)、求 的度数;(2)、将 绕点 逆时针旋转100°,点 的对应点为点 ,连接 ,求证:四边形 为平行四边形.22. 越野汽车轮胎的质量是根据其正常使用的时间来衡量,使用时间越长,表明质量越好,且使用时间大于或等于7千小时的为优质品,否则为普通品.某汽修店对 , 两种不同型号的汽车轮胎做试验,各随机抽取部分产品作为样本,得到试验结果的扇形统计图和折线图如图所示.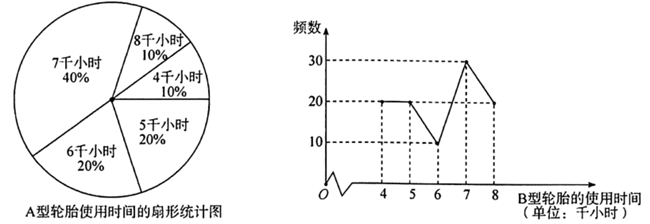
根据上述调查数据,解决下列问题:
(1)、现从仓库中大量的 , 两种型号的轮胎中各随机抽取1件产品,求其中至少有1件是优质品的概率;(2)、汽修店对轮胎实行“三包”,根据多年销售经验可知,轮胎每件产品的利润 (单位:元)与其使用时间 (单位:千小时)的关系如表:使用时间 (单位:千小时)
每件产品的利润 (单位:元)
-200
200
400
请从平均利润角度考虑,该汽修店应选择销售哪种轮胎,说明理由.
23. 如图,菱形 中, , 为对角线, 是边 延长线上一点,连接 . (1)、在线段 上求作点 ,使得 (要求:尺规作图,保留痕迹,不写作法);(2)、在(1)的作图条件下,直线 交直线 与点 ,求证: , , 三点共线.
(1)、在线段 上求作点 ,使得 (要求:尺规作图,保留痕迹,不写作法);(2)、在(1)的作图条件下,直线 交直线 与点 ,求证: , , 三点共线.