广东省惠州市仲恺区三校联考2021-2022学年九年级上学期数学第一次月考试卷

试卷更新日期：2021-10-19 类型：月考试卷

进入出卷网下载

一、单选题

1. 关于x的一元二次方程（a﹣2）x²+x﹣a²+4＝0的一个根为0，则a的值是（　　）

A、2或﹣2 B、2 C、﹣2 D、1

查看试题解析
2. 将抛物线y＝﹣3x²先向左平移1个单位长度，再向下平移2个单位长度，得到的抛物线的解析式是（）

A、y＝﹣3（x﹣1）²﹣2 B、y＝﹣3（x﹣1）²+2 C、y＝﹣3（x+1）²﹣2 D、y＝﹣3（x+1）²+2

查看试题解析
3. 若关于x的一元二次方程 $k x^{2} - 2 x - 3 = 0$ 有实数根，则字母k的取值范围是（）

A、 $k ⩾ - \frac{1}{2}$ B、 $k ⩾ - \frac{1}{2}$ 且 $k \neq 0$ C、 $k ⩾ - \frac{1}{3}$ D、 $k ⩾ - \frac{1}{3}$ 且 $k \neq 0$

查看试题解析
4. 下列对二次函数 $y = x^{2} - x$ 的图象的描述，正确的是（）

A、开口向下 B、对称轴是 $y$ 轴 C、经过原点 D、在对称轴右侧 $y$ 随 $x$ 的增大而减小

查看试题解析
5. 若用配方法解一元二次方程 $x^{2} - 4 x - 5 = 0$ ，则方程可变形为（　　）

A、 ${(x + 2)}^{2} = 9$ B、 ${(x - 2)}^{2} = 9$ C、 ${(x + 2)}^{2} = 1$ D、 ${(x - 2)}^{2} = 1$

查看试题解析
6. 参加足球联赛的每两队之间都进行一场比赛，共要比赛90场，设共有 $x$ 个队参加比赛，则下列方程正确的是（）

A、 $\frac{1}{2} x (x + 1) = 90$ B、 $x (x + 1) = 90$ C、 $\frac{1}{2} x (x - 1) = 90$ D、 $x (x - 1) = 90$

查看试题解析
7. 顶点为 $(6, 0)$ ，开口向下，开口的大小与函数 $y = \frac{1}{3} x^{2}$ 的图象相同的抛物线所对应的函数是（）

A、 $y = \frac{1}{3} {(x + 6)}^{2}$ B、 $y = \frac{1}{3} {(x - 6)}^{2}$ C、 $y = - \frac{1}{3} {(x + 6)}^{2}$ D、 $y = - \frac{1}{3} {(x - 6)}^{2}$

查看试题解析
8. 二次函数 $y = a x^{2} + b x + c$ 与一次函数 $y = a x + c$ 在同一坐标系内的图象可能是图（）

A、 B、 C、 D、

查看试题解析
9. 如图是二次函数y=ax²+bx+c（a，b，c是常数，a≠0）图象的一部分，与x轴的交点A在点（2，0）和（3，0）之间，对称轴是x=1．对于下列说法：①ab＜0；②2a+b=0；③3a+c＞0；④a+b≥m（am+b）（m为实数）；⑤当﹣1＜x＜3时，y＞0，其中正确的是（）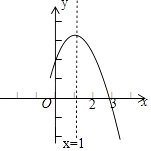

A、①②④ B、①②⑤ C、②③④ D、③④⑤

查看试题解析
10. 对于代数式: $x^{2} - 2 x + 2$ ，下列说法正确的是（）

A、有最大值 $1$ B、有最小值 $1$ C、有最小值 $2$ D、无法确定最大最小值

查看试题解析

二、填空题

11. 抛物线 $y = - x^{2} + 5$ 的顶点坐标是．

查看试题解析
12. 已知一个三角形的三边都是方程 $x^{2} - 8 x + 12 = 0$ 的根，则此三角形的周长为．

查看试题解析
13. 设A（﹣2， $y_{1}$ ），B（1， $y_{2}$ ），C（2， $y_{3}$ ）是抛物线 $y = - x^{2} - 2 x + 2$ 上的三点，则 $y_{1} ， y_{2} ， y_{3}_{}$ 的大小关系为.（用“>”连接）

查看试题解析
14. 已知m，n是一元二次方程 $x^{2} - 3 x + 2 = 0$ 的两个实数根，则 $2 m^{2} - 4 m n - 6 m$ 的值为．

查看试题解析
15. 已知抛物线 $y = a x^{2} + b x + c$ 过 $(- 1 ， 1)$ 和 $(5 ， 1)$ 两点，那么该抛物线的对称轴是直线．

查看试题解析
16. 抛物线的部分图像如图所示，当y＞0，则x的取值范围是．

查看试题解析
17. 已知二次函数 $y = x^{2} - 4 a x + 4 a^{2} + a - 1$ （ $a$ 为常数），当 $a$ 取不同的值时，其图象构成一个“抛物线系”．如图分别是当 $a = t_{1}$ ， $a = t_{2}$ ， $a = t_{3}$ ， $a = t_{4}$ 时二次函数的图象，它们的顶点在一条直线上，则这条直线的解析式是．

查看试题解析

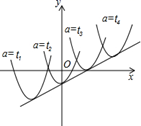
三、解答题

18. 解一元二次方程：

(1)、 $x^{2} + 2 x - 2 = 0$

(2)、 $2 x^{2} - 5 x - 3 = 0$

查看试题解析
19. 抛物线y=-x²+bx+c过点（0，-3）和（2，1），试确定抛物线的解析式，并求出抛物线与x轴的交点坐标．

查看试题解析
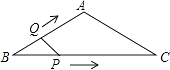
20. 用配方法把二次函数y=﹣2x²+6x+4化为y=a（x+m）²+k的形式，再指出该函数图象的开口方向、对称轴和顶点坐标．

查看试题解析
21. 如图，在等腰△ABC中，AB=AC=4cm，∠B=30°，点P从点B出发，以 $\sqrt{3}$ cm/s的速度沿BC方向
运动到点C停止，同时点Q从点B出发，以1cm/s的速度沿BA-AC方向运动到点C停止，若△BPQ的面积为y（cm²），运动时间为x（s），求在这一运动过程中y与x之间函数关系式.

查看试题解析
22. 某口罩生产厂生产的口罩1月份平均日产量为30000个，1月底因突然爆发新冠肺炎疫情，市场对口罩需求量大增，为满足市场需求，厂决定从2月份起扩大产量，3月份平均日产量达到36300个.

(1)、求口罩日产量的月平均增长率；

(2)、按照这个增长率，预计4月份平均日产量为多少？

查看试题解析
23. 已知关于x的一元二次方程 $x^{2} + 2 x + a - 2 = 0$ ．

(1)、若该方程有两个实数根，求实数a的取值范围；

(2)、若该方程的一个根为1，求a的值及该方程的另一根．

查看试题解析
24. 某商店经销一种销售成本为每千克40元的水产品，据市场分析，若按每千克50元销售，一个月能售出500千克；销售单价每涨1元，月销售量就减少10千克，针对这种海产品的销售情况，请解答以下问题：

(1)、当销售单价定为每千克55元时，月销售量是千克，月销售利润是元；

(2)、设销售单价为每千克x元，月销售利润为y，请你求出y与x之间的函数关系式；

(3)、商店想在月销售成本不超过10000元的情况下，使得月销售利润达到8000元，销售单价应该定为多少元？

查看试题解析
25. 如图，已知抛物线 $y = - x^{2} + b x + c$ 与一直线相交于 $A (- 1 ， 0)$ ， $C (2 ， 3)$ 两点，与y轴交于点N．其顶点为D．

(1)、抛物线及直线 $A C$ 的函数关系式；

(2)、若抛物线的对称轴与直线 $A C$ 相交于点B，E为直线 $A C$ 上的任意一点，过点E作 $E F / / B D$ 交抛物线于点F，以B，D，E，F为顶点的四边形能否为平行四边形？若能，求点E的坐标；若不能，请说明理由；

(3)、若P是抛物线上位于直线 $A C$ 上方的一个动点，求 $△ A P C$ 的面积的最大值．

(4)、设点M的坐标为 $(3 ， m)$ ，直接写出使 $M N + M D$ 的和最小时m的值．

查看试题解析