广东省佛山市云东海街道三校联考2021-2022学年九年级上学期数学第一次月考试卷

试卷更新日期：2021-10-19 类型：月考试卷

进入出卷网下载

一、单选题

1. 用配方法解一元二次方程2x²﹣x﹣1=0时，配方正确的是（）

A、（x﹣ $\frac{1}{4}$ ）²= $\frac{9}{16}$ B、（x+ $\frac{1}{4}$ ）²= $\frac{9}{16}$ C、（x﹣ $\frac{1}{2}$ ）²= $\frac{5}{4}$ D、（x+ $\frac{1}{2}$ ）²= $\frac{5}{4}$

查看试题解析
2. 如图，在矩形ABCD中，对角线AC与BD相交于点O.点E、F分别是AB，AO的中点，且AC＝8，则EF的长度为（）

A、2 B、4 C、6 D、8

查看试题解析
3. 在一个不透明的袋中装有2个黄球和2个红球，它们除颜色外没有其他区别，从袋中任意摸出一个球，然后放加搅匀，再从袋中任意摸一个球，那么两次都摸到黄球的概率是（）

A、 $\frac{1}{8}$ B、 $\frac{1}{6}$ C、 $\frac{1}{4}$ D、 $\frac{1}{2}$

查看试题解析
4. 若关于x的一元二次方程mx²﹣2x+1＝0有两个实数根，则实数m的取值范围是(　　)

A、m≤1 B、m≤﹣1 C、m≤1且m≠0 D、m≥1且m≠0

查看试题解析
5. 如图，在平面直角坐标系中，菱形ABCD的顶点A在 $y$ 轴上，顶点B ， C的坐标分别为(−6，0)，(4，0)，则点 $D$ 的坐标是（）

A、 $(6 ， 8)$ B、 $(10 ， 8)$ C、 $(10 ， 6)$ D、 $(4 ， 6)$

查看试题解析
6. 一个三角形的三边长都是方程 $x^{2} - 7 x + 10 = 0$ 的根，则这个三角形的周长不可能是 $($ $)$

A、6 B、9 C、12 D、15

查看试题解析
7. 如图，D、E、F分别是 $△ A B C$ 各边中点，则以下说法错误的是（）

A、 $△ B D E$ 和 $△ D C F$ 的面积相等 B、四边形 $A E D F$ 是平行四边形 C、若 $A B = B C$ ，则四边形 $A E D F$ 是菱形 D、若 $∠ A = 90 °$ ，则四边形 $A E D F$ 是矩形

查看试题解析
8. 我国南宋数学家杨辉曾提出这样一个问题：“直田积（矩形面积），八百六十四（平方步），只云阔（宽）不及长一十二步（宽比长少12步），问阔及长各几步．“如果设矩形田地的长为x步，那么同学们列出的下列方程中正确的是（）

A、x(x+12)=864 B、x(x-12)=864 C、x²+12x=864 D、x²+12x-864=0

查看试题解析
9. 如图，将矩形纸片ABCD的两个直角进行折叠，使CB，AD恰好落在对角线AC上，B′，D′分别是B，D的对应点，折痕分别为CF，AE.若AB＝4，BC＝3，则线段 $B^{'} D^{'}$ 的长是（）

A、 $\frac{5}{2}$ B、2 C、 $\frac{3}{2}$ D、1

查看试题解析
10. 如图，在菱形ABCD中，AB=AC=1，点E、F分别为边AB、BC上的点，且AE=BF，连接CE、AF交于点H，连接DH交AC于点O，则下列结论：①△ABF≌△CAE；②∠FHC=∠B；③△ADO≌△ACH；④ $S_{菱形 A B C D} = \sqrt{3}$ ；其中正确的结论个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 若关于x的方程（a+3）x^|a|-1﹣3x+2=0是一元二次方程，则a的值为．

查看试题解析
12. 如图，菱形ABCD的对角线AC ， BD相交于点O ，过点A作AH⊥BC于点H ，连接OH ，若OB＝6，菱形ABCD的面积为48，则OH的长为．

查看试题解析
13. 在一个不透明的袋中装有除颜色外其余均相同的 $n$ 个小球，其中有6个黑球，从袋中随机摸出一球，记下其颜色，称为一次摸球试验，之后把它放回袋中，搅匀后，再继续摸出一球，利用计算机模拟的结果，摸出黑球的频率在0.5附近波动，由此可以估计出 $n$ 的值是.

查看试题解析
14. 某商店今年7月份的销售额是5万元，9月份的销售额是7.2万元，从7月份到9月份该店销售额平均每月的增长率是.

查看试题解析
15. 设a，b是方程 $x^{2} - x - 2020 = 0$ 的两个实数根，则 $a^{2} - 2 a - b$ 的值为.

查看试题解析
16. 如图，矩形 $A B C D$ 中， $A B = 8$ ，点 $E$ 是 $A D$ 上的一点，且 $A E = 4$ ， $B E$ 的垂直平分线交 $B C$ 的延长线于点 $F$ ，连结 $E F$ 交 $C D$ 于点 $G$ ．若 $G$ 是 $C D$ 的中点，则 $B C$ 的长是．

查看试题解析
17. 如图，在四边形 $A B C D$ 中， $A B / / C D$ ， $∠ C = 90^{\circ}$ °， $A B = 8$ ， $A D = C D = 5$ ，点 $M 、 N$ 分别为 $B C 、 A B$ 上的动点（含端点）， $E 、 F$ 分别为 $D M 、 M N$ 的中点，则 $E F$ 长度的最小值为．

查看试题解析

三、解答题

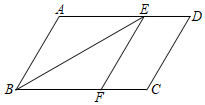
18. 解一元二次方程：

(1)、x²﹣9＝0；

(2)、x²﹣2x﹣3＝0．

查看试题解析
19. 已知：如图，在▱ABCD中，点E、F分别在AD、BC上，且BE平分∠ABC，EF∥AB.求证：四边形ABFE是菱形.

查看试题解析
20. 已知关于x的一元二次方程x²﹣3x+k＝0方程有两实根x₁和x₂ ．

(1)、求实数k的取值范围；

(2)、当x₁和x₂是一个矩形两邻边的长且矩形的对角线长为 $\sqrt{5}$ ，求k的值．

查看试题解析
21. 目前，全国各地正在有序推进新冠疫苗接种工作．某单位为了解职工对疫苗接种的关注度，随机抽取了部分职工进行问卷调查，调查结果分为：A（实时关注）、B（关注较多）、C（关注较少）、D（不关注）四类，现将调查结果绘制成如图所示的统计图．

请根据图中信息，解答下列问题：

(1)、求C类职工所对应扇形的圆心角度数，并补全条形统计图；

(2)、若D类职工中有3名女士和2名男士，现从中任意抽取2人进行随访，请用树状图或列表法求出恰好抽到一名女士和一名男士的概率．

查看试题解析
22. 如图，在四边形 $A B C D$ 中， $A D / / B C$ ， $∠ C = 90 °$ ， $∠ A D B = ∠ A B D = \frac{1}{2} ∠ B D C$ ， $D E$ 交 $B C$ 于点 $E$ ，过点 $E$ 作 $E F ⊥ B D$ ，垂足为 $F$ ，且 $E F = E C$ .

(1)、求证：四边形 $A B E D$ 是菱形；

(2)、若 $A D = 4$ ，求 $△ B E D$ 的面积.

查看试题解析
23. “疫情”期间，某商场积压了一批商品，现欲尽快清仓，确定降价促销．据调查发现，若每件商品盈利50元时，可售出500件，商品单价每下降1元，则可多售出20件．设每件商品降价x元．

(1)、每件商品降价x元后，可售出商品件（用含x的代数式表示）．

(2)、若要使销售该商品的总利润达到28000元，求x的值．

(3)、销售该商品的总利润能否达到30000元？若能，请求出此时的单价；若不能，请说明理由．

查看试题解析
24. 如图，在△ABC中，∠B=90°，AB=5cm，BC=7cm，点P从点A开始沿AB边向点B以1cm/s的速度移动，点Q从点B开始沿BC边向点C以2cm/s的速度移动．

(1)、如果P ， Q分别从A ， B同时出发，经过几秒后，△PBQ的面积等于4cm²？

(2)、如果P ， Q分别从A ， B同时出发，经过几秒后，PQ的长度等于 $2 \sqrt{10}$ cm？

(3)、在（1）中，△PQB的面积能否等于7cm²？说明理由．

查看试题解析
25. 在 $Δ A B C$ 中， $∠ B A C = 90^{°} ， A B = A C$ ，点 $D$ 为直线 $B C$ 上一动点（点 $D$ 不与 $B ， C$ 重合），以 $A D$ 为边在 $A D$ 右侧作正方形 $A D E F$ ，连接 $C F$

(1)、探究猜想如图1，当点 $D$ 在线段 $B C$ 上时，
① $B C$ 与 $C F$ 的位置关系为；

② $B C ， C D ， C F$ 之间的数量关系为；

(2)、深入思考：如图2，当点 $D$ 在线段 $C B$ 的延长线上时，结论①、②是否仍然成立？若成立，请给予证明；若不成立，请你写出符合题意结论再给予证明．

(3)、拓展延伸如图3，当点 $D$ 在线段 $B C$ 的延长线上时，正方形 $A D E F$ 对角线交于点 $O$ ．若已知 $A B = 2 \sqrt{2} ， C D = \frac{1}{4} B C$ ，请求出 $O C$ 的长．

查看试题解析