广东省佛山市杨和镇三校联考2021-2022学年九年级上学期数学第一次月考试卷
试卷更新日期:2021-10-19 类型:月考试卷
一、单选题
-
1. 若关于 的一元二次方程 有一个根为0,则 ( )A、1 B、﹣3或1 C、﹣3 D、3或﹣12. 如图,四边形ABCD的对角线互相平分,要使它变为菱形,需要添加的条件是( )
 A、AB=CD B、AD=BC C、AC=BD D、AB=BC3. 用配方法解方程x2+10x+9=0,变形后的结果正确的是( )A、(x+10)2=9 B、(x+10)2=16 C、(x+5)2=9 D、(x+5)2=164. 一个菱形的两条对角线的长度分别是6 cm和8 cm,这个菱形的面积是( )A、12 cm2 B、14 cm2 C、24 cm2 D、48 cm25. 一个盒子里装有除颜色外都相同的3个球,其中2个红球,1个白球,现从盒子里随意摸出1个不放回,再摸出1个,两次均摸到红球的概率是( )A、 B、 C、 D、6. 若关于x的一元二次方程kx2-x+3=0有两个实数根,则k的取值范围是( )A、k≤12 B、k≤ C、k≤12且k≠0 D、k≤ 且k≠07. 如图,在矩形 中, , ,点 在边 上,若 平分 ,则 ( )
A、AB=CD B、AD=BC C、AC=BD D、AB=BC3. 用配方法解方程x2+10x+9=0,变形后的结果正确的是( )A、(x+10)2=9 B、(x+10)2=16 C、(x+5)2=9 D、(x+5)2=164. 一个菱形的两条对角线的长度分别是6 cm和8 cm,这个菱形的面积是( )A、12 cm2 B、14 cm2 C、24 cm2 D、48 cm25. 一个盒子里装有除颜色外都相同的3个球,其中2个红球,1个白球,现从盒子里随意摸出1个不放回,再摸出1个,两次均摸到红球的概率是( )A、 B、 C、 D、6. 若关于x的一元二次方程kx2-x+3=0有两个实数根,则k的取值范围是( )A、k≤12 B、k≤ C、k≤12且k≠0 D、k≤ 且k≠07. 如图,在矩形 中, , ,点 在边 上,若 平分 ,则 ( )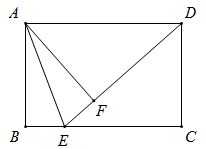 A、 B、 C、 D、8. 在元旦庆祝活动中,参加活动的同学互赠贺卡,共送贺卡42张,设参加活动的同学有 人,根据题意,可列方程( )A、 B、 C、 D、9. 如图,在矩形 中, , .点E为射线 上的一个动点, 与 关于直线 对称,当 为直角三角形时,则 的长为( )
A、 B、 C、 D、8. 在元旦庆祝活动中,参加活动的同学互赠贺卡,共送贺卡42张,设参加活动的同学有 人,根据题意,可列方程( )A、 B、 C、 D、9. 如图,在矩形 中, , .点E为射线 上的一个动点, 与 关于直线 对称,当 为直角三角形时,则 的长为( )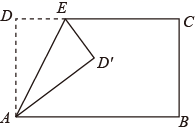 A、2或18 B、3或18 C、3或2 D、2或810. 如图,正方形 和正方形 的顶点 在同一直线 上,且 ,给出下列结论: , , 的面积 ,其中正确的个数为( )
A、2或18 B、3或18 C、3或2 D、2或810. 如图,正方形 和正方形 的顶点 在同一直线 上,且 ,给出下列结论: , , 的面积 ,其中正确的个数为( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
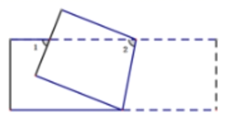
11. 如图,将一条两边平行的纸带折叠,当∠2=80°,则∠1=.
 12. 已知代数式 与代数式 的值互为相反数,则 的值为.13. 在一个不透明的盒子中装有红、白两种除颜色外完全相同的球,其中有a个白球和15个红球,若每次将球充分搅匀后,任意摸出1个球记下颜色后再放回盒子,通过大量重复试验后,发现摸到红球的频率稳定在0.3左右,则a的值约为 .14. 设 、 是方程 的两个实数根,则 的值为 .15. 若2是方程x2﹣2kx+3=0的一个根,则方程的另一根为 .16. 如图,△ABC中,∠B=90°,AB=6cm,BC=8cm,点P从A点开始沿AB向B点以1cm/s的速度移动,点Q从B点开始沿BC边向C点以2cm/s的速度移动.如果P、Q分别从A、B同时出发,经过秒钟△PQB的面积等于△ABC面积的 .
12. 已知代数式 与代数式 的值互为相反数,则 的值为.13. 在一个不透明的盒子中装有红、白两种除颜色外完全相同的球,其中有a个白球和15个红球,若每次将球充分搅匀后,任意摸出1个球记下颜色后再放回盒子,通过大量重复试验后,发现摸到红球的频率稳定在0.3左右,则a的值约为 .14. 设 、 是方程 的两个实数根,则 的值为 .15. 若2是方程x2﹣2kx+3=0的一个根,则方程的另一根为 .16. 如图,△ABC中,∠B=90°,AB=6cm,BC=8cm,点P从A点开始沿AB向B点以1cm/s的速度移动,点Q从B点开始沿BC边向C点以2cm/s的速度移动.如果P、Q分别从A、B同时出发,经过秒钟△PQB的面积等于△ABC面积的 . 17. 如图,在矩形 中, , ,对角线 , 相交于点 , 为边 上一动点,连接 .若 为等腰三角形,则 的长为 .
17. 如图,在矩形 中, , ,对角线 , 相交于点 , 为边 上一动点,连接 .若 为等腰三角形,则 的长为 .
三、解答题
-
18. 选用适当方法解方程:(1)、x2﹣4x﹣5=0;(2)、3x2+x﹣1=0.19. 某地区2013年投入教育经费2500万元,2015年投入教育经费3025万元.(1)、求2013年至2015年该地区投入教育经费的年平均增长率(2)、根据(1)所得的年平均增长率,预计2016年该地区将投入教育经费多少万元20. 已知关于 的一元二次方程 有两个实数根 和 .(1)、求实数 的取值范围;(2)、当 时,求 的值.21. 已知:如图,在平行四边形ABCD中,∠ABC的平分线交AD于点E,过点A作BE的垂线交BE于点F,交BC于点G,连接EG,CF.
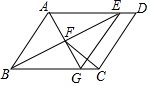 (1)、求证:四边形ABGE是菱形;(2)、若∠ABC=60°,AB=4,AD=5,求CF的长.22. “垃圾分类”越来越受到人们的关注,我市某中学对部分学生就“垃圾分类”知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.根据图中信息回答下列问题:
(1)、求证:四边形ABGE是菱形;(2)、若∠ABC=60°,AB=4,AD=5,求CF的长.22. “垃圾分类”越来越受到人们的关注,我市某中学对部分学生就“垃圾分类”知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.根据图中信息回答下列问题: (1)、接受问卷调查的学生共有人,条形统计图中 的值为;(2)、扇形统计图中“了解很少”部分所对应扇形的圆心角的度数为;(3)、若从对垃圾分类知识达到“非常了解”程度的2名男生和2名女生中随机抽取2人参加垃圾分类知识竞赛,请用列表或画树状图的方法,求恰好抽到1名男生和1名女生的概率.23. 某超市准备进一批季节性小家电,每个进价为40元,经市场预测,销售定价为每个50元,可售出400个;定价每增加1元,销售量将减少10个,设每个定价增加x元,(1)、当定价增加5元时,获利是多少元?(2)、商店若准备获得利润6000元,并且使进货量较少,则每个定价为多少元?应进货多少个?24. 如图1,在矩形纸片 中, , ,折叠纸片使 点落在边 上的 处,折痕为 .过点 作 交 于 ,连接 .
(1)、接受问卷调查的学生共有人,条形统计图中 的值为;(2)、扇形统计图中“了解很少”部分所对应扇形的圆心角的度数为;(3)、若从对垃圾分类知识达到“非常了解”程度的2名男生和2名女生中随机抽取2人参加垃圾分类知识竞赛,请用列表或画树状图的方法,求恰好抽到1名男生和1名女生的概率.23. 某超市准备进一批季节性小家电,每个进价为40元,经市场预测,销售定价为每个50元,可售出400个;定价每增加1元,销售量将减少10个,设每个定价增加x元,(1)、当定价增加5元时,获利是多少元?(2)、商店若准备获得利润6000元,并且使进货量较少,则每个定价为多少元?应进货多少个?24. 如图1,在矩形纸片 中, , ,折叠纸片使 点落在边 上的 处,折痕为 .过点 作 交 于 ,连接 . (1)、求证:四边形 是菱形;(2)、如图2,当 在 边上移动时,折痕的端点 也随着移动,当点 与点 重合时,求菱形 的面积.25. 如图,在平面直角坐标系中,一次函数y=﹣ x+4的图象与x轴和y轴分别相交于A、B两点.动点P从点A出发,在线段AO上以每秒3个单位长度的速度向点O作匀速运动,到达点O停止运动,点A关于点P的对称点为点Q,以线段PQ为边向上作正方形PQMN.设运动时间为t秒.
(1)、求证:四边形 是菱形;(2)、如图2,当 在 边上移动时,折痕的端点 也随着移动,当点 与点 重合时,求菱形 的面积.25. 如图,在平面直角坐标系中,一次函数y=﹣ x+4的图象与x轴和y轴分别相交于A、B两点.动点P从点A出发,在线段AO上以每秒3个单位长度的速度向点O作匀速运动,到达点O停止运动,点A关于点P的对称点为点Q,以线段PQ为边向上作正方形PQMN.设运动时间为t秒. (1)、当t= 秒时,点Q的坐标是;(2)、在运动过程中,设正方形PQMN与△AOB重叠部分的面积为S,求S与t的函数表达式;(3)、若正方形PQMN对角线的交点为T,请直接写出在运动过程中OT+PT的最小值.
(1)、当t= 秒时,点Q的坐标是;(2)、在运动过程中,设正方形PQMN与△AOB重叠部分的面积为S,求S与t的函数表达式;(3)、若正方形PQMN对角线的交点为T,请直接写出在运动过程中OT+PT的最小值.