广东省佛山市芦苞镇五校联考2021-2022学年九年级上学期数学第一次月考试卷
试卷更新日期:2021-10-19 类型:月考试卷
一、单选题
-
1. 下列方程中,一定是关于x的一元二次方程的是( )A、ax2+bx+c=0 B、x2+3=0 C、 + =1 D、x2+2-x(x-1)=02. 下列说法正确的是( )A、一组对边相等且有一个角是直角的四边形是矩形 B、对角线互相垂直的四边形是菱形 C、对角线相等且互相垂直的四边形是正方形 D、对角线平分一组对角的平行四边形是菱形3. 一元二次方程 ,配方后可形为( )A、 B、 C、 D、4. 在平行四边形ABCD中,下列结论中,错误的是( )A、 B、 C、当 时,平行四边形ABCD是菱形 D、当 ,平行四边形ABCD是矩形5. 若m , n是方程x2+2019x﹣2020=0的两个实数根,则m+n﹣mn的值为( )A、﹣4039 B、﹣1 C、1 D、40396. 在四张反面无差别的卡片上,其正面分别印有线段、等边三角形、平行四边形和正六边形.现将四张卡片的正面朝下放置,混合均匀后从中随机抽取两张,则抽到的卡片正面图形都是轴对称图形的概率为( )A、 B、 C、 D、7. 如图,菱形ABCD中,E是AD的中点,将△CDE沿CE折叠后,点A和点D恰好重合,若菱形ABCD的面积为4 ,则菱形ABCD的周长是( )
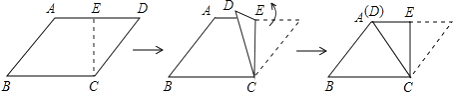 A、8 B、16 C、8 D、168. 要组织一次篮球比赛,赛制为单循环形式(每两队之间都赛一场),计划安排15场比赛,设应邀请x个球队参加比赛,根据题意可列方程为( )A、x(x﹣1)=15 B、x(x+1)=15 C、 =15 D、 =159. 把边长为3的正方形 绕点A顺时针旋转45°得到正方形 ,边 与 交于点O,则四边形 的周长是( )
A、8 B、16 C、8 D、168. 要组织一次篮球比赛,赛制为单循环形式(每两队之间都赛一场),计划安排15场比赛,设应邀请x个球队参加比赛,根据题意可列方程为( )A、x(x﹣1)=15 B、x(x+1)=15 C、 =15 D、 =159. 把边长为3的正方形 绕点A顺时针旋转45°得到正方形 ,边 与 交于点O,则四边形 的周长是( ) A、6 B、 C、 D、10. 如图所示,所有的四边形都是正方形,所有三角形都是等腰直角三角形,且最大的正方形的边长为4.若按照图①至图③的规律设计图案,则在第 个图中所有等腰直角三角形的面积和为( )
A、6 B、 C、 D、10. 如图所示,所有的四边形都是正方形,所有三角形都是等腰直角三角形,且最大的正方形的边长为4.若按照图①至图③的规律设计图案,则在第 个图中所有等腰直角三角形的面积和为( )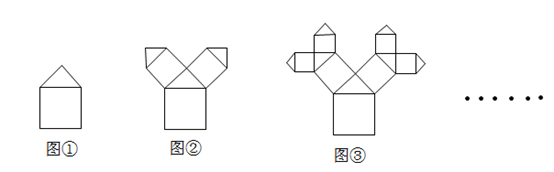 A、 B、 C、 D、32
A、 B、 C、 D、32二、填空题
-
11. 若0是一元二次方程(m﹣1)x2+6x+m2﹣1=0的一个根,则m的值为;12. 在菱形ABCD中,对角线AC=30,BD=60,则菱形ABCD的面积为 .13. 已知等腰 ABC的三条边长都是方程x2-9x+18=0的根,则 ABC的周长为;14. 一个不透明的口袋中装有2个红球和若干个白球,它们除颜色外其它完全相同.通过多次摸球实验后发现,摸到红球的频率稳定在20%附近,口袋中白球最有可能有个;15. 方程x2+2kx+k2﹣2k+1=0的两个实数根x1 , x2满足x12+x22=4,则k的值为 .16. 如图1,直角三角形纸片的一条直角边长为6,剪四块这样的直角三角形纸片,把它们按图2放入一个边长为10 的正方形中(纸片在结合部分不重叠无缝隙),则图2中阴影部分面积为
 17. 如图,正方形ABCD的边长为3,点E在边AB上,且 .若点P在对角线BD上移动,则 的最小值是 .
17. 如图,正方形ABCD的边长为3,点E在边AB上,且 .若点P在对角线BD上移动,则 的最小值是 .
三、解答题
-
18. 解下列方程:(1)、x2﹣6x+3=0;(2)、3x(x﹣2)=2(x﹣2).19. 在一个不透明的盒子中装有三张卡片,分别标有数字为1,2,7,这些卡片除数字不同外其余均相同.洗匀后,小强从盒子中随机抽取一张卡片记下数字后放回,洗匀后再随机抽取一张卡片.用画树状图或列表的方法,求两次抽取的卡片上数字之和为偶数的概率.
20. 如图,小华要为一个长3分米,宽2分米的长方形防疫科普电子小报四周添加一个边框,要求边框的四条边宽度相等,且边框面积与电子小报内容所占面积相等,小华添加的边框的宽度应是多少分米? 21. 如图,四边形ABCD是边长为2的正方形,点G是BC延长线上一点,连接AG , 点E、F分别在AG上,连接BE、DF , ∠1=∠2,∠3=∠4.
21. 如图,四边形ABCD是边长为2的正方形,点G是BC延长线上一点,连接AG , 点E、F分别在AG上,连接BE、DF , ∠1=∠2,∠3=∠4.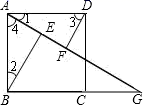 (1)、证明:△ABE≌△DAF;(2)、若∠AGB=30°,求EF的长.22. 目前,全国各地正在有序推进新冠疫苗接种工作.某单位为了解职工对疫苗接种的关注度,随机抽取了部分职工进行问卷调查,调查结果分为:A(实时关注)、B(关注较多)、C(关注较少)、D(不关注)四类,现将调查结果绘制成如图所示的统计图.
(1)、证明:△ABE≌△DAF;(2)、若∠AGB=30°,求EF的长.22. 目前,全国各地正在有序推进新冠疫苗接种工作.某单位为了解职工对疫苗接种的关注度,随机抽取了部分职工进行问卷调查,调查结果分为:A(实时关注)、B(关注较多)、C(关注较少)、D(不关注)四类,现将调查结果绘制成如图所示的统计图.
请根据图中信息,解答下列问题:
(1)、求C类职工所对应扇形的圆心角度数,并补全条形统计图;(2)、若D类职工中有3名女士和2名男士,现从中任意抽取2人进行随访,请用树状图或列表法求出恰好抽到一名女士和一名男士的概率.23. 超市销售某种儿童玩具,经市场调查发现,每件利润为 元时,每天可售出 件;销售单价每增加 元,每天销售量会减少 件.物价管理部门规定,该种玩具每件利润不得超过 元.设销售单价增加 元,每天可售出 件.(1)、写出 与 之间的函数关系式(不要求写出自变量取值范围);(2)、当 取何值时,超市每天销售这种玩具可获得利润 元?此时每天可销售多少件?24. 如图1,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm,点P由点B出发沿BA方向向点A匀速运动,速度为1cm/s;点Q由点A出发沿AC方向向点C匀速运动,速度为2cm/s;连结PQ . 若设运动时间为t(s)(0<t<2),解答下列问题: (1)、当t为何值时?PQ//BC?(2)、设△APQ的面积为y(cm2),求y与t之间的函数关系?(3)、是否存在某一时刻t , 使线段PQ恰好把△ABC的周长和面积同时平分?若存在求出此时t的值;若不存在,说明理由.(4)、如图2,连结PC , 并把△PQC沿AC翻折,得到四边形PQP'C , 那么是否存在某一时刻t , 使四边形PQP'C为菱形?若存在求出此时t的值;若不存在,说明理由.25. 如图①所示,已知A、B为直线l上两点,点C为直线l上方一动点,连接AC、BC,分别以AC、BC为边向△ABC外作正方形CADF和正方形CBEG,过点D作DD1⊥l于点D1 , 过点E作EE1⊥l于点E1 .
(1)、当t为何值时?PQ//BC?(2)、设△APQ的面积为y(cm2),求y与t之间的函数关系?(3)、是否存在某一时刻t , 使线段PQ恰好把△ABC的周长和面积同时平分?若存在求出此时t的值;若不存在,说明理由.(4)、如图2,连结PC , 并把△PQC沿AC翻折,得到四边形PQP'C , 那么是否存在某一时刻t , 使四边形PQP'C为菱形?若存在求出此时t的值;若不存在,说明理由.25. 如图①所示,已知A、B为直线l上两点,点C为直线l上方一动点,连接AC、BC,分别以AC、BC为边向△ABC外作正方形CADF和正方形CBEG,过点D作DD1⊥l于点D1 , 过点E作EE1⊥l于点E1 .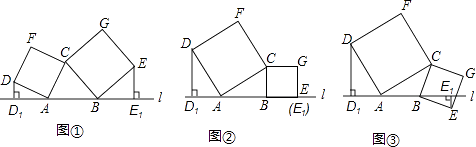 (1)、如图②,当点E恰好在直线l上时(此时E1与E重合),试说明DD1=AB;(2)、在图①中,当D、E两点都在直线l的上方时,试探求三条线段DD1、EE1、AB之间的数量关系,并说明理由;(3)、如图③,当点E在直线l的下方时,请直接写出三条线段DD1、EE1、AB之间的数量关系.(不需要证明)
(1)、如图②,当点E恰好在直线l上时(此时E1与E重合),试说明DD1=AB;(2)、在图①中,当D、E两点都在直线l的上方时,试探求三条线段DD1、EE1、AB之间的数量关系,并说明理由;(3)、如图③,当点E在直线l的下方时,请直接写出三条线段DD1、EE1、AB之间的数量关系.(不需要证明)