广东省佛山市龙江镇三校联考2021-2022学年九年级上学期数学第一次月考试卷

试卷更新日期：2021-10-19 类型：月考试卷

进入出卷网下载

一、单选题

1. 下列说法中错误的是（）

A、平行四边形的对角相等 B、菱形的邻边相等 C、平行四边形的对角线互相平分 D、菱形的对角线互相垂直且相等

查看试题解析
2. 下列配方正确的是（）

A、 $x^{2} + 2 x + 5 = {(x + 1)}^{2} + 6$ B、 $x^{2} + 3 x = {(x + \frac{3}{2})}^{2} - \frac{3}{2}$ C、 $3 x^{2} + 6 x + 1 = 3 {(x + 1)}^{2} - 2$ D、 $x^{2} - \frac{1}{2} x + \frac{3}{4} = {(x - \frac{1}{4})}^{2} + \frac{1}{16}$

查看试题解析
3. 广东省2021年的高考采用“ $3 + 1 + 2$ ”模式：“3”是指语文、数学、外语3科为必选科目，“1”是指在物理、历史2科中任选1科，“2”是指在化学、生物、思想政治、地理4科中任选2科．若小红在“1”中选择了历史，则她在“2”中选地理、生物的概率是（）

A、 $\frac{1}{6}$ B、 $\frac{1}{3}$ C、 $\frac{1}{4}$ D、 $\frac{1}{2}$

查看试题解析
4. 若关于x的一元二次方程ax²﹣2x+1=0有两个实数根，则实数a的取值范围是（）

A、a≤1且a≠0 B、a＜1且a≠0 C、a≤1 D、a＜1

查看试题解析
5. 如图，菱形 $A B C D$ 的对角线 $A C$ 、 $B D$ 相交于点 $O$ ，过点 $D$ 作 $D H ⊥ A B$ 于点 $H$ ，连接 $O H$ ，若 $O A = 3$ ， $O H = 2$ .则菱形 $A B C D$ 的面积为（）

A、12 B、10 C、6 D、24

查看试题解析
6. 若m、n是一元二次方程x²＋3x﹣9＝0的两个根，则 $m^{2} + 4 m + n$ 的值是（）

A、4 B、5 C、6 D、12

查看试题解析
7. 学校初二年级组织足球联赛，赛制为单循环制（每两个队之间比赛一场).共进行了 $28$ 场比赛，问初二年级有几个参赛班级？设初二年级有 $x$ 个班级参加比赛.根据题意列出方程正确的是（）

A、 $x^{2} = 28$ B、 $\frac{1}{2} x (x - 1) = 28$ C、 $\frac{1}{2} x^{2} = 28$ D、 $x (x - 1) = 28$

查看试题解析
8. 菱形ABCD的一条对角线的长为6，边AB的长是方程 $x^{2} - 7 x + 12 = 0$ 的一个根，则菱形ABCD的周长为（）

A、16 B、12 C、12或16 D、无法确定

查看试题解析
9. 如图，在矩形 $A B C D$ 中， $A B = 5$ ， $B C = 6$ ，点M，N分别在 $A D$ ， $B C$ 上，且 $A M = B N$ ， $A D = 3 A M$ ，E为 $B C$ 边上一动点，连接 $D E$ ，将 $△ D C E$ 沿 $D E$ 所在直线折叠得到 $△ D C' E$ ，当 $C'$ 点恰好落在线段 $M N$ 上时， $C E$ 的长为（）

A、 $\frac{5}{2}$ 或2 B、 $\frac{5}{2}$ C、 $\frac{3}{2}$ 或2 D、 $\frac{3}{2}$

查看试题解析
10. 如图，在矩形ABCD中，O为AC中点，EF过O点且EF⊥AC分别交DC于F ，交AB于E ，点G是AE中点且∠AOG＝30°，①DC＝3OG；②OG＝ $\frac{1}{2}$ BC；③△OGE是等边三角形；④S_△AOE＝ $\frac{1}{6}$ S矩形ABCD ，则下列结论正确的个数为（　　）

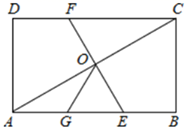A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 若 $x_{1}$ 、 $x_{2}$ 是方程 $x^{2} - 5 x = 0$ 的两根，则x₁+x₂=.

查看试题解析
12. 在一个不透明的暗箱中装有红、黄、蓝三种除颜色外完全相同的小球，其中红球5个，黄球7个，蓝球a个.若每次将球充分搅匀后，随机摸出一个小球记下颜色后，放回盒子里，经过大量的重复试验后发现，摸到红球的频率稳定在25%左右，则a的值约为.

查看试题解析
13. 对于任意实数a、b，定义一种运算： $a \otimes b = a^{2} + b^{2} - a b$ ，若 $x \otimes (x - 1) = 3$ ，则x的值为.

查看试题解析
14. 如图，在边长为2的菱形ABCD中，DE⊥AB于点E ，连接CE ，若AE＝BE ，则CE的长是．

查看试题解析
15. 关于x的一元二次方程 $x^{2} + m x - 5 = 0$ 有一根是 $x = - 1$ ，则另外一根是.

查看试题解析
16. 如图，矩形 $A B C D$ 的对角线 $A C$ ， $B D$ 相交于点 $O$ ， $A E // B D$ ， $D E // A C$ ．若 $A C = 5$ ，则四边形 $A O D E$ 的周长为．

查看试题解析
17. 如图，点 $E$ 、 $F$ 分别在正方形 $A B C D$ 的边 $A D$ 、 $D C$ 上， $A E = D F = 2$ ， $B E$ 与 $A F$ 相交于点 $G$ ，点 $H$ 为 $B F$ 的中点，连接 $G H$ ，若 $G H$ 的长为 $\frac{\sqrt{34}}{2}$ ，则正方形的边长为．

查看试题解析

三、解答题

18. 解方程：

(1)、（x+1）²＝16；

(2)、2x²﹣5x+3＝0.

查看试题解析
19. 已知：如图，四边形ABCD是平行四边形，AE⊥BC，AF⊥CD，垂足分别是E，F，且BE＝DF．

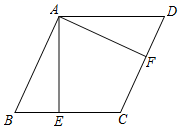(1)、求证：△ABE≌△ADF；

(2)、求证：四边形ABCD是菱形．

查看试题解析
20. 已知两个整式 $A = x^{2} + 2 x$ ， $B = x + 2$ ．

(1)、若 $B$ 的值是1，求 $x$ 和 $A$ 的值；

(2)、若 $A + B$ 的值是0，求 $x$ 的值．

查看试题解析
21. 某学校计划利用一片空地建一个学生自行车车棚，其中一面靠墙，这堵墙的长度为12米.计划建造车棚的面积为80平方米，已知现有的木板材料可使新建板墙的总长为28米.

(1)、这个车棚的长和宽分别应为多少米？

(2)、如图，为了方便学生取车，施工单位决定在车棚内修建几条等宽的小路，使得停放自行车的面积为54平方米，那么小路的宽度是多少米？

查看试题解析

22. 为庆祝中国共产党成立100周年，某校举行党史知识竞赛活动．赛后随机抽取了部分学生的成绩，按得分划分为A、B、C、D四个等级，并绘制了如下不完整的统计表和统计图．

等级	成绩（x）	人数
A	$90 \leq x \leq 100$	15
B	$80 \leq x < 90$	a
C	$70 \leq x < 80$	18
D	$x < 70$	7

根据图表信息，回答下列问题：

(1)、表中

a =

；扇形统计图中，C等级所占的百分比是；D等级对应的扇形圆心角为度；若全校共有1800名学生参加了此次知识竞赛活动，请估计成绩为A等级的学生共有人．

(2)、若95分以上的学生有4人，其中甲、乙两人来自同一班级，学校将从这4人中随机选出两人参加市级比赛，请用列表或树状图法求甲、乙两人至少有1人被选中的概率

查看试题解析

23. 随着全球疫情的爆发，医疗物资需求猛增，某企业及时引进一条口罩生产线生产口罩，开工第一天生产口罩5000盒，第三天生产口罩7200盒，若每天增长的百分率相同．

(1)、求每天增长的百分率.

(2)、经调查发现，1条生产线的最大产能是15000盒/天，但是每增加1条生产线，每条生产线的产能将减少500盒/天，现该厂要保证每天生产口罩65000盒，在增加产能的同时又要节省投入的条件下（生产线越多，投入越大），应该增加几条生产线？

查看试题解析
24. 如图，在菱形ABCD中，AB=2，∠ABC=60°，对角线AC、BD相交于点O，将对角线AC所在的直线绕点O顺时针旋转角α，（0°＜α＜90°）后得到直线l，直线l与AD、BC的两边相交于点E、F．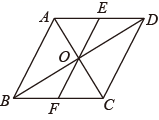

(1)、求证：△AOE≌△COF；

(2)、当α=30°时，求线段EF的长；

(3)、当α=60°时，直接写出四边形EOCD的面积．

查看试题解析
25. 如图①，在矩形 $O A C B$ 中，点 $A$ 、 $B$ 分别在 $x$ 轴、 $y$ 轴正半轴上，点 $C$ 在第一象限， $O A = 8$ ， $O B = 6$ ．

(1)、请直接写出点 $C$ 的坐标；

(2)、如图②，点 $F$ 在 $B C$ 上，连接 $A F$ ，把 $△ A C F$ 沿着 $A F$ 折叠，点 $C$ 刚好与线段 $A B$ 上一点 $C^{'}$ 重合，求线段 $C F$ 的长度；

(3)、如图③，点 $P (x ， y)$ 为直线 $y = 2 x - 6$ 在第一象限内的图象上的个动点，点 $D$ 在线段 $A C$ 上（不与点 $A$ 、 $C$ 重合），是否存在直角顶点为 $P$ 的等腰直角 $△ B D P$ ，若存在，请求出点 $P$ 的坐标：若不存在，请说明理由．

查看试题解析