广东省佛山市白石镇三校联考2021-2022学年九年级上学期数学第一次月考试卷

试卷更新日期：2021-10-19 类型：月考试卷

进入出卷网下载

一、单选题

1. 下列命题中是真命题的是（）

A、一组对边平行，另一组对边相等的四边形是平行四边形 B、对角线互相垂直且平分的四边形是菱形 C、一个角为90°且一组邻边相等的四边形是正方形 D、对角线互相垂直且相等的四边形是矩形

查看试题解析
2. 将方程 $x^{2} - 4 x - 3 = 0$ 的左边配成完全平方式后，得到的方程为：（）

A、 ${(x - 2)}^{2} = 7$ B、 ${(x - 2)}^{2} = 3$ C、 ${(x - 2)}^{2} = - 7$ D、 ${(x - 2)}^{2} = - 3$

查看试题解析
3. 已知关于x的一元二次方程 $a x^{2} - 4 x - 1 = 0$ 有两个不相等的实数根，则a的取值范围是（）

A、 $a \geq - 4$ B、 $a > - 4$ C、 $a \geq - 4$ 且 $a \neq 0$ D、 $a > - 4$ 且 $a \neq 0$

查看试题解析
4. 等腰三角形的底边长为6，腰长是方程 $x^{2} - 8 x + 15 = 0$ 的一个根，则该等腰三角形的周长为（）

A、12 B、16 C、l2或16 D、15

查看试题解析
5. 某班同学毕业时都将自己的照片向全班其他同学各送一张表示留念，全班共送1035张照片，如果全班有x名同学，根据题意，列出方程为（）

A、x（x+1）=1035 B、x（x﹣1）=1035×2 C、x（x﹣1）=1035 D、2x（x+1）=1035

查看试题解析

二、填空题

6. 已知 $(m - 2) x^{| m |} + x = 1$ 是关于x的一元二次方程，则m可取的值是.

查看试题解析
7. 如图，在菱形ABCD中，点E在CD上，若AE＝AC ， ∠B＝48°，则∠BAE的大小为．

查看试题解析
8. 在一个不透明袋子里有1个红球、1个黄球、n个白球，除颜色外其余都相同，每次摇匀后随机摸出一个小球，记下颜色后再放回袋中，经过大量重复摸球试验后发现摸到白球的频率稳定在0.5左右，则n的值为

查看试题解析
9. 一个菱形的边长是方程 $x^{2} - 8 x + 15 = 0$ 的一个根，其中一条对角线长为8，则菱形的面积为；

查看试题解析
10. 如图，在正方形 $A B C D$ 中， $E ， F$ 分别是 $A B ， A D$ 的中点，若 $E F = 2$ ，则 $A C$ 的长是．

查看试题解析
11. 设m，n分别为一元二次方程 $x^{2} - 2 x - 2020 = 0$ 的两个实数根，则 $m^{2} - m + n$ ＝.

查看试题解析
12. 如图，在菱形 $A B C D$ 中， $∠ A B C = 30 °$ ， $A D = 6$ ，点P ， M分别是边 $A B$ 和对角线 $B D$ 上的动点，则 $A M + P M$ 的最小值为．

查看试题解析

三、解答题

13. 解方程：

(1)、 $x^{2} + 4 x = 0$ ；

(2)、 ${(2 x - 1)}^{2} = 4 x - 2$ ．

查看试题解析
14. 已知关于x的方程x²＋（2k－1）x＋k²－1＝0.

(1)、若方程有两个不相等的实数根，求k的取值范围；

(2)、若方程的两根恰好是一个矩形两邻边的长，且k＝－2，求该矩形的对角线L的长.

查看试题解析
15. 随着手机的日益普及，学生使用手机给学校管理和学生发展带来诸多不利影响，为了保护学生视力，防止学生沉迷网络和游戏，让学生在学校专心学习，促进学生身心健康发展，教育部办公厅于2021年1月15日颁发了《教育部办公厅关于加强中小学生手机管理工作的通知》，为贯彻《通知》精神、某学校团委组织了“我与手机说再见”为主题的演讲比赛，根据参赛同学的得分情况绘制了如图所示的两幅不完整的统计图．（其中A表示“一等奖”，B表示“二等奖”，C表示“三等奖”，D表示“优秀奖”）

请你根据统计图中所提供的信息解答下列问题：

(1)、获奖总人数为人， $m =$ ；

(2)、请将条形统计图补充完整；

(3)、学校将从获得一等奖的4名同学（其中有一名男生，三名女生）中随机抽取两名参加全市的比赛，请利用树状图或列表法求抽取同学中恰有一名男生和一名女生的概率．

查看试题解析
16. 2020年秋冬以来，由于全国大葱种植面积的减少与产量的减产，10月份到12月份，大葱的批发价格持续走高。10月份大葱的批发价格为5元/公斤，12月份大葱的批发价格涨到7.2元/公斤．

(1)、求10月份到12月份大葱批发价格的月平均增长率；

(2)、进入12月份以来，某农贸市场按照7.2元/公斤的批发价购进大葱进行销售，销售价格为10元/公斤，每天能销售大葱500公斤，为了扩大销售，增加盈利，最大限度让利于顾客，该农贸市场决定对大葱进行降价销售，根据市场调查发现，大葱的销售单价每降低0.1元，每天的销售量将增加40公斤，求当大葱的销售价格降低多少元时，该农贸市场每天销售大葱的利润为1640元？

查看试题解析
17. 如图，在 $▱ A B C D$ 中，G、H分别是 $A D$ 、 $B C$ 的中点，E、O、F是对角线AC的四等分点，顺次连接G、E、H、F ．

(1)、求证：四边形 $G E H F$ 是平行四边形；

(2)、若 $A C = 2 A B$ ，则四边形 $G E H F$ 是形；

(3)、当 $A C$ 、 $A B$ 满足时，四边形 $G E H F$ 是正方形．

查看试题解析
18. 如图1，把一个含45°角的直角三角板ECF和一个正方形ABCD摆放在一起，使三角板的直角顶点和正方形的顶点C重合，点E、F分别在正方形边CB、CD上，连接AF ，取AF中点M ， EF的中点N ，连接MD、MN ．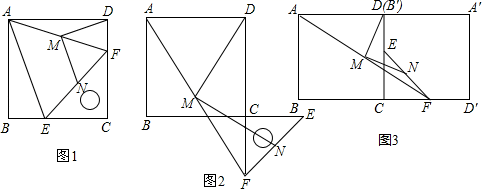

(1)、连接AE ，则△AEF是三角形，MD、MN的数量关系是．

(2)、如图2，将图1中的直角三角板ECF绕点C顺时针旋转180°，其他条件不变，则MD、MN的数量关系还成立吗？若成立，请加以证明；若不成立，请说明理由．

(3)、将图1中正方形ABCD及直角三角板ECF同时绕点C顺时针旋转90°，如图3，其他条件不变，则MD、MN的数量关系还成立吗？若成立，请加以证明；若不成立，请说明理由．

查看试题解析