广东省东莞市茶山镇五校联考2021-2022学年九年级上学期数学第一次月考试卷
试卷更新日期:2021-10-19 类型:月考试卷
一、单选题
-
1. 下列方程是一元二次方程的是( )A、 B、 C、 D、2. 用配方法将 变形,正确的是( )
A、 B、 C、 D、3. 在平面直角坐标系中,将抛物线 先向右平移2个单位,再向上平移2个单位,得到的抛物线解析式为( )A、 B、 C、 D、4. 关于x的一元二次方程 的一个根是0,则 的值是( )A、−3或1 B、1 C、−3 D、5. 关于x的一元二次方程﹣kx2﹣6x+3=0有两个不相等的实数根,则k的取值范围是( )A、k>﹣3 B、k<3 C、k<3且k≠0 D、k>﹣3且k≠06. 如图,已知抛物线 与直线 交于 , 两点,则关于 的不等式 的解集是( )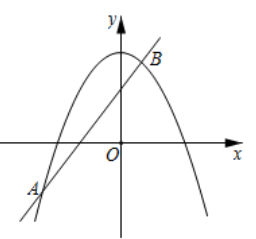 A、 或 B、 或 C、 D、7. 某超市一月份的营业额为200万元,三月份的营业额为288万元,如果每月比上月增长的百分数相同,则平均每月的增长率为( )A、10% B、15% C、20% D、25%8. 二次函数 的图象与一次函数 在同一平面直角坐标系中的图象可能是( )A、
A、 或 B、 或 C、 D、7. 某超市一月份的营业额为200万元,三月份的营业额为288万元,如果每月比上月增长的百分数相同,则平均每月的增长率为( )A、10% B、15% C、20% D、25%8. 二次函数 的图象与一次函数 在同一平面直角坐标系中的图象可能是( )A、 B、
B、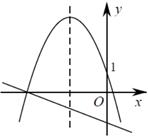 C、
C、 D、
D、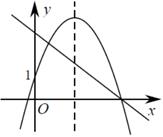 9. 二次函数 的图象如图所示,对称轴为 .给出以下结论:① ;② ;③ ;④ .其中,正确的结论有( )
9. 二次函数 的图象如图所示,对称轴为 .给出以下结论:① ;② ;③ ;④ .其中,正确的结论有( )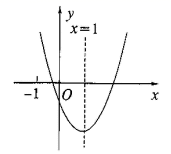 A、1个 B、2个 C、3个 D、4个10. 如图,平面直角坐标系中,抛物线y= x2-2x+3交x轴于点B,C,交y轴于点A,点P(x,y)是抛物线上的一个动点,连接PA,AC,PC,记△ACP面积为S.当y≤3时,S随x变化的图象大致是( )
A、1个 B、2个 C、3个 D、4个10. 如图,平面直角坐标系中,抛物线y= x2-2x+3交x轴于点B,C,交y轴于点A,点P(x,y)是抛物线上的一个动点,连接PA,AC,PC,记△ACP面积为S.当y≤3时,S随x变化的图象大致是( )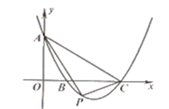 A、
A、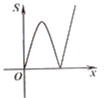 B、
B、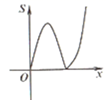 C、
C、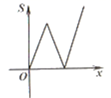 D、
D、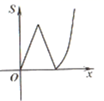
二、填空题
-
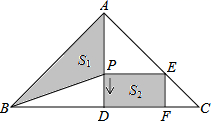
11. 抛物线y=2(x-3)2+1的顶点坐标为 .12. 抛物线 的对称轴为直线 .13. 已知点 都在抛物线 上,若 ,则 .(填“>”、“<”或“=”)14. 若直角三角形的两直角边长分别是方程x2﹣14x+48=0的两根,则该直角三角形的面积是 .15. 已知m、n是方程x2+3x﹣2=0的两个实数根,则3mn+n+m的值为.16. 将二次函数 的图象向左平移1个单位,再向上平移1个单位若得到的函数图象与直线 有两个交点,则a的取值范围是.17. 如图,在Rt△ABC中,∠BAC=90°,AB=AC=16cm , AD为BC边上的高,动点P从点A出发,沿A→D方向以 cm/s的速度向点D运动,过P点作PE∥BC交AC于点E , 过E点作EF⊥BC于点F , 设△ABP的面积为S1 , 四边形PDFE的面积为S2 , 则点P在运动过程中,S1+S2的最大值为 .
三、解答题
-
18. 解方程: .19. 如图,进行绿地的长、宽各增加xm.
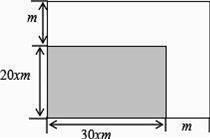 (1)、写出扩充后的绿地的面积y( )与x(m)之间的函数关系式;(2)、若扩充后的绿地面积y是原矩形面积的2倍,求x的值.20. 如图,二次函数y=(x-2)2+m的图象与y轴交于点C,点B是点C关于该二次函数图象的对称轴对称的点,已知一次函数y=kx+b的图象上的点A(1,0)及B.
(1)、写出扩充后的绿地的面积y( )与x(m)之间的函数关系式;(2)、若扩充后的绿地面积y是原矩形面积的2倍,求x的值.20. 如图,二次函数y=(x-2)2+m的图象与y轴交于点C,点B是点C关于该二次函数图象的对称轴对称的点,已知一次函数y=kx+b的图象上的点A(1,0)及B.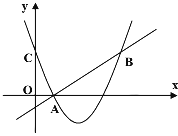 (1)、求二次函数与一次函数的解析式;
(1)、求二次函数与一次函数的解析式;
(2)、根据图象,写出满足kx+b≤(x-2)2+m的x的取值范围.21. 已知二次函数的图象以A(﹣1,4)为顶点,且过点B(2,﹣5).(1)、求该函数的关系式;(2)、求当横坐标取﹣3和1时所对应的函数值;(3)、根据(2)计算,直接写出当x的值在什么范围时,所对应的函数值大于0.22. 甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图,甲在O点正上方1m的P处发出一球,羽毛球飞行的高度y(m)与水平距离x(m)之间满足函数表达式y=a(x﹣4)2+h,已知点O与球网的水平距离为5m,球网的高度为1.55m.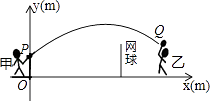 (1)、当a=﹣ 时,
(1)、当a=﹣ 时,①求h的值;
②通过计算判断此球能否过网.
(2)、若甲发球过网后,羽毛球飞行到与点O的水平距离为7m,离地面的高度为 m的Q处时,乙扣球成功,求a的值.23. 超市销售某种儿童玩具,如果每件利润为40元(市场管理部门规定,该种玩具每件利润不能超过60元),每天可售出50件.根据市场调查发现,销售单价每增加2元,每天销售量会减少1件.设销售单价增加 元,每天售出 件.(1)、请写出 与 之间的函数表达式;(2)、当 为多少时,超市每天销售这种玩具可获利润2250元?(3)、设超市每天销售这种玩具可获利 元,当 为多少时 最大,最大值是多少?24. 如图,抛物线y=ax2+bx+c与x轴交于点A和B(1,0),与y轴交于点C,直线y= x﹣2经过A,C两点,抛物线的顶点为D.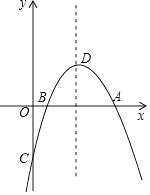 (1)、求抛物线的解析式和顶点D的坐标;(2)、在y轴上是否存在一点G,使得GD+GB的值最小?若存在,求出点G的坐标;若不存在,请说明理由;(3)、在抛物线的对称轴上是否存在点P,使△PAB是以AB为腰的等腰三角形?若存在,求出P点坐标;若不存在,请说明理由.25. 已知二次函数 与一次函数 ,(1)、求证:对任意的实数k , 函数m与n的图象总有两个交点(2)、设 与 的图象相交于 两点,m的图象与y轴相交于点C,记 与 的面积分别为 (O为坐标原点),求证: 总是定值;(3)、对于二次函数m,是否存在实数 ,使得当 时,恰好有 ,若存在,请求出 的值;若不存在,请说明理由.
(1)、求抛物线的解析式和顶点D的坐标;(2)、在y轴上是否存在一点G,使得GD+GB的值最小?若存在,求出点G的坐标;若不存在,请说明理由;(3)、在抛物线的对称轴上是否存在点P,使△PAB是以AB为腰的等腰三角形?若存在,求出P点坐标;若不存在,请说明理由.25. 已知二次函数 与一次函数 ,(1)、求证:对任意的实数k , 函数m与n的图象总有两个交点(2)、设 与 的图象相交于 两点,m的图象与y轴相交于点C,记 与 的面积分别为 (O为坐标原点),求证: 总是定值;(3)、对于二次函数m,是否存在实数 ,使得当 时,恰好有 ,若存在,请求出 的值;若不存在,请说明理由.