北京一七一中2021-2022学年九年级上学期数学10月月考试卷
试卷更新日期:2021-10-19 类型:月考试卷
一、单选题
-
1. 彩陶、玉器、青铜器等器物以及壁画、织锦上美轮美奂的纹样,穿越时空,向人们呈现出古代中国丰富多彩的物质与精神世界,各种纹样经常通过平移、旋转、轴对称以及其它几何构架连接在一起,形成复杂而精美的图案.以下图案纹样中,从整体观察(个别细微之处的细节忽略不计),大致运用了旋转进行构图的是( )
A、 B、
B、 C、
C、 D、
D、 2. 二次三项式x2﹣3x+2的二次项系数,一次项系数,常数项分别是( )A、0,-3,2 B、0,-3,-2 C、1,-3,2 D、1,3,23. 若x=1是方程x2+ax﹣2=0的一个根,则a的值为( )A、0 B、1 C、2 D、34. 用配方法解一元二次方程x2+4x﹣6=0,此方程可变形为( )A、(x+2)2=10 B、(x﹣2)2=10 C、(x+2)2=2 D、(x﹣2)2=25. 二次函数 的顶点坐标是( )A、(1,-3) B、(-1,-3) C、(1,3) D、(-1,3)6. 如图,一块含30°角的直角三角板ABC绕点C顺时针旋转到△A′B′C , 当B , C , A′在一条直线上时,三角板ABC的旋转角度为( )
2. 二次三项式x2﹣3x+2的二次项系数,一次项系数,常数项分别是( )A、0,-3,2 B、0,-3,-2 C、1,-3,2 D、1,3,23. 若x=1是方程x2+ax﹣2=0的一个根,则a的值为( )A、0 B、1 C、2 D、34. 用配方法解一元二次方程x2+4x﹣6=0,此方程可变形为( )A、(x+2)2=10 B、(x﹣2)2=10 C、(x+2)2=2 D、(x﹣2)2=25. 二次函数 的顶点坐标是( )A、(1,-3) B、(-1,-3) C、(1,3) D、(-1,3)6. 如图,一块含30°角的直角三角板ABC绕点C顺时针旋转到△A′B′C , 当B , C , A′在一条直线上时,三角板ABC的旋转角度为( )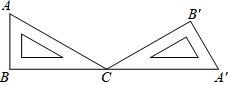 A、150° B、120° C、60° D、30°7. 商店销售一种进价为50元/件的商品,售价为60元/件,每星期可卖出200件,若每件商品的售价上涨1元,则每星期就会少卖10件.每件商品的售价上涨x元(x正整数),每星期销售的利润为y元,则y与x的函数关系式为( )A、y=10(200﹣10x) B、y=200(10+x) C、y=10(200﹣10x)2 D、y=(10+x)(200﹣10x)8. 若关于x的一元二次方程x2+4x+m=0有两个不相等的实数根,则m的取值范围是( )A、m>﹣4 B、m>4 C、m≤﹣4 D、m<49. 已知二次函数 的部分图象如图所示,则使得函数值 大于 的自变量 的取值可以是( )
A、150° B、120° C、60° D、30°7. 商店销售一种进价为50元/件的商品,售价为60元/件,每星期可卖出200件,若每件商品的售价上涨1元,则每星期就会少卖10件.每件商品的售价上涨x元(x正整数),每星期销售的利润为y元,则y与x的函数关系式为( )A、y=10(200﹣10x) B、y=200(10+x) C、y=10(200﹣10x)2 D、y=(10+x)(200﹣10x)8. 若关于x的一元二次方程x2+4x+m=0有两个不相等的实数根,则m的取值范围是( )A、m>﹣4 B、m>4 C、m≤﹣4 D、m<49. 已知二次函数 的部分图象如图所示,则使得函数值 大于 的自变量 的取值可以是( ) A、-4 B、-2 C、0 D、210. 已知二次函数y=a(x﹣1)2﹣4,当﹣1≤x≤4时,y的最大值是5,则a的值是( )A、﹣1 B、﹣2 C、1 D、2
A、-4 B、-2 C、0 D、210. 已知二次函数y=a(x﹣1)2﹣4,当﹣1≤x≤4时,y的最大值是5,则a的值是( )A、﹣1 B、﹣2 C、1 D、2二、填空题
-
11. 已知 是关于x的一元二次方程,则m=.12. 将抛物线y=2x2向下平移1个单位后得到新的抛物线的表达式为 .13. 如图,当△AED绕正方形ABCD的顶点D旋转到与△DCF重合时,∠DEF的度数为 .
 14. 某公司最近的各项经营中,一季度的营业额为50万元,第三季度的营业额为950万元,如果平均每季度营业额的增长率相同,求这个增长率,设这个增长率为x , 则所列的方程应为 .15. 已知二次函数y=(x﹣2)2+1,若点A(0,y1)和B(1,y2)在此函数图象上,则y1与y2的大小关系是:y1y2 .16. 如图,在△ABC中,∠ACB=90°,将△ABC绕点A顺时针旋转90°,得到△ADE , 连接BD , 若AC=3,DE=1,则线段BD的长为 .
14. 某公司最近的各项经营中,一季度的营业额为50万元,第三季度的营业额为950万元,如果平均每季度营业额的增长率相同,求这个增长率,设这个增长率为x , 则所列的方程应为 .15. 已知二次函数y=(x﹣2)2+1,若点A(0,y1)和B(1,y2)在此函数图象上,则y1与y2的大小关系是:y1y2 .16. 如图,在△ABC中,∠ACB=90°,将△ABC绕点A顺时针旋转90°,得到△ADE , 连接BD , 若AC=3,DE=1,则线段BD的长为 . 17. 甲、乙、丙三人进行乒乓球单打训练,每局两人进行比赛,第三个人做裁判,每一局都要分出胜负,胜方和原来的裁判进行新一局的比赛,输方转做裁判,依次进行.半天训练结束时,发现甲共当裁判4局,乙、丙分别打了9局、14局比赛,在这半天的训练中,甲、乙、丙三人共打了局比赛,其中第7局比赛的裁判是 .
17. 甲、乙、丙三人进行乒乓球单打训练,每局两人进行比赛,第三个人做裁判,每一局都要分出胜负,胜方和原来的裁判进行新一局的比赛,输方转做裁判,依次进行.半天训练结束时,发现甲共当裁判4局,乙、丙分别打了9局、14局比赛,在这半天的训练中,甲、乙、丙三人共打了局比赛,其中第7局比赛的裁判是 .三、解答题
-
18. 点P(2,﹣1)关于原点对称点的坐标是 .19. 解方程:2x2﹣3x+1=0.20. 如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,△ABC的顶点都在格点上,建立平面直角坐标系,以原点O为中心,将△ABC顺时针旋转90°,得到△A1B1C1 .
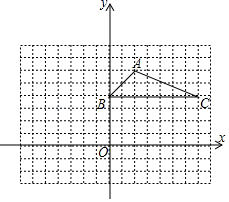 (1)、请在网格内画出△A1B1C1 .(2)、写出点A1的标 , 点B1的坐标 , 点C1的坐标 .21. 已知m是方程x2﹣x﹣1=0的一个根,代数式5m2﹣5m+2016的值.22. 如图,利用一面墙(墙长为10m),用20m长的篱笆,怎样围成一个面积为48m2的矩形场地?
(1)、请在网格内画出△A1B1C1 .(2)、写出点A1的标 , 点B1的坐标 , 点C1的坐标 .21. 已知m是方程x2﹣x﹣1=0的一个根,代数式5m2﹣5m+2016的值.22. 如图,利用一面墙(墙长为10m),用20m长的篱笆,怎样围成一个面积为48m2的矩形场地?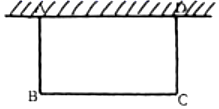 23. 已知二次函数y=x2﹣2x﹣3.
23. 已知二次函数y=x2﹣2x﹣3. (1)、求出该二次函数图象顶点坐标;(2)、求图象与两坐标轴的交点坐标;(3)、结合函数图象,直接写出y<0时x的取值范围.24. 已知关于 的一元二次方程 .(1)、求证:该方程总有两个实数根;(2)、若 ,且该方程的两个实数根的差为2,求 的值.25. 如图,在平面直角坐标系xOy中,二次函数y=x2+bx+c的图象与x轴y轴的交点分别为(1,0)和(0,﹣3).
(1)、求出该二次函数图象顶点坐标;(2)、求图象与两坐标轴的交点坐标;(3)、结合函数图象,直接写出y<0时x的取值范围.24. 已知关于 的一元二次方程 .(1)、求证:该方程总有两个实数根;(2)、若 ,且该方程的两个实数根的差为2,求 的值.25. 如图,在平面直角坐标系xOy中,二次函数y=x2+bx+c的图象与x轴y轴的交点分别为(1,0)和(0,﹣3). (1)、求此二次函数的表达式;(2)、结合函数图象当﹣4<x<1时,直接写出y的取值范围.26. 在平面直角坐标系 中,抛物线 .(1)、若抛物线过点 ,求抛物线的对称轴;(2)、若 为抛物线上两个不同的点.
(1)、求此二次函数的表达式;(2)、结合函数图象当﹣4<x<1时,直接写出y的取值范围.26. 在平面直角坐标系 中,抛物线 .(1)、若抛物线过点 ,求抛物线的对称轴;(2)、若 为抛物线上两个不同的点.①当 时, ,求a的值;
②若对于 ,都有 ,求a的取值范围.
27. 在△ABC中,∠BAC=45°,CD⊥AB于点D , AE⊥BC于点E , 连接DE .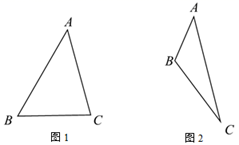 (1)、如图1,当△ABC为锐角三角形时,
(1)、如图1,当△ABC为锐角三角形时,①依题意补全图形,猜想∠BAE与∠BCD之间的数量关系并证明;
②用等式表示线段AE , CE , DE的数量关系,并证明;
(2)、如图2,当∠ABC为钝角时,依题意补全图形并直接写出线段AE , CE , DE的数量关系.28. 在平面直角坐标系 中,对于点 和图形 ,如果以 为端点的任意一条射线与图形 最多只有一个公共点,那么称点 独立于图形 .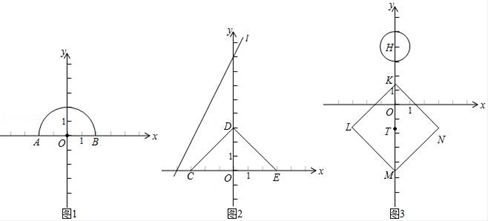 (1)、如图1,已知点 ,以原点 为圆心, 长为半径画弧交 轴正半轴于点 .在 , , , 这四个点中,独立于弧 的点是;(2)、如图2,已知点 , , ,点 是直线 上的一个动点.若点 独立于折线 ,求点 的横坐标 的取值范围;(3)、如图3,⊙ 是以点 为圆心,半径为1的圆.点 在y轴上且 ,以点 为中心的正方形 的顶点K的坐标为 ,将正方形 在 轴及 轴上方的部分记为图形 .若⊙ 上的所有点都独立于图形 ,直接写出 的取值范围.
(1)、如图1,已知点 ,以原点 为圆心, 长为半径画弧交 轴正半轴于点 .在 , , , 这四个点中,独立于弧 的点是;(2)、如图2,已知点 , , ,点 是直线 上的一个动点.若点 独立于折线 ,求点 的横坐标 的取值范围;(3)、如图3,⊙ 是以点 为圆心,半径为1的圆.点 在y轴上且 ,以点 为中心的正方形 的顶点K的坐标为 ,将正方形 在 轴及 轴上方的部分记为图形 .若⊙ 上的所有点都独立于图形 ,直接写出 的取值范围.