安徽省淮南市西部地区2021-2022学年九年级上学期数学第一次月考试卷
试卷更新日期:2021-10-19 类型:月考试卷
一、单选题
-
1. 把方程x(x+2)=5x化成一般式,则a、b、c的值分别是( )A、1,3,5 B、1,–3,0 C、–1,0,5 D、1,3,02. 抛物线 的顶点坐标是( )A、(﹣1,2) B、(﹣1,﹣2) C、(1,﹣2) D、(1,2)3. 方程 的左边配成完全平方后所得方程为( )A、 B、 C、 D、4. 关于x的方程(a﹣1)x2+ x+2=0是一元二次方程,则a的取值范围是( )A、a≠1 B、a≥-1且a≠1 C、a>-1且a≠1 D、a≠±15. 已知关于x的一元二次方程kx2﹣2x+3=0有两个不相等的实数根,则k的取值范围是( )A、k< B、k>﹣ C、k>﹣ 且k≠0 D、k< 且k≠06. 若一个三角形的两边长分别为2和6,第三边是方程x2-8x+15=0的一根,则这个三角形的周长为( )A、5 B、3或5 C、13 D、11或137. 在一次酒会上,每两人都只碰一次杯,如果一共碰杯55次,则参加酒会的人数为( )A、9人 B、10人 C、11人 D、12人8. 在同一平面直角坐标系中,函数y=ax2+b与y=bx2+ax的图象可能是( )A、
 B、
B、 C、
C、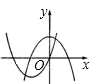 D、
D、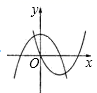 9. 已知抛物线 具有如下性质:抛物线上任意一点到定点F(0,2)的距离与到x轴的距离相等,点M的坐标为(3,6),P是抛物线 上一动点,则△PMF周长的最小值是( )
9. 已知抛物线 具有如下性质:抛物线上任意一点到定点F(0,2)的距离与到x轴的距离相等,点M的坐标为(3,6),P是抛物线 上一动点,则△PMF周长的最小值是( ) A、5 B、9 C、11 D、1310. 已知二次函数y=ax2+bx+c(a≠0)图象上部分点的坐标(x , y)的对应值如表所示,则方程ax2+bx+1.365=0的根是( )
A、5 B、9 C、11 D、1310. 已知二次函数y=ax2+bx+c(a≠0)图象上部分点的坐标(x , y)的对应值如表所示,则方程ax2+bx+1.365=0的根是( )x
……
0
4
……
y
……
0.365
-1
0.365
……
A、0或4 B、 或4 C、1或5 D、 或 2二、填空题
-
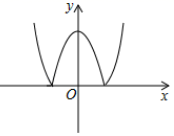
11. 方程x(x﹣2)=x的根是 .12. 已知 是方程 的一个根,则代数式 的值为 .13. 抛物线y=2(x﹣1)2+c过(﹣2,y1),(0,y2),( ,y3)三点,则y1 , y2 , y3大小关系是 .14. 已知函数y=|x2﹣4|的大致图象如图所示,那么:方程|x2﹣4|=m . (m为实数)
①若该方程恰有3个不相等的实数根,则m的值是 .
②若该方程恰有2个不相等的实数根,则m的取值范围是 .
三、解答题
-
15. 解方程:x2+x﹣2=0.16. 二次函数图象过A(﹣1,0),B(2,0),C(0,﹣2)三点,求此抛物线的解析式.17. 当m为何值时,关于x的方程 为一元二次方程,并求这个一元二次方程的解.18. 把抛物线y=ax2+bx+c先向右平移3个单位长度,再向下平移2个单位长度,所得抛物线是y=x2﹣3x+5,求a+b+c的值.19. 已知关于x的方程 .(1)、当该方程的一个根为1时,求a的值及该方程的另一根;(2)、求证:不论a取何实数,该方程都有两个不相等的实数根.20. 某商店经销一批小商品,每件商品的成本为8元.据市场分析,销售单价定为10元时,每天能售出200件;现采用提高商品售价,减少销售量的办法增加利润,若销售单价每涨1元,每天的销售量就减少20件.
设销售单价定为x元.据此规律,请回答:
(1)、商店日销售量减少件,每件商品盈利元(用含x的代数式表示);(2)、针对这种小商品的销售情况,该商店要保证每天盈利640元,同时又要使顾客得到实惠,那么销售单价应定为多少元?21. 如图是二次函数y=(x+m)2+k的图象,其顶点坐标为M(1,﹣4)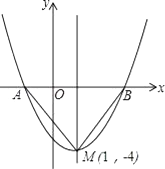 (1)、求出图象与x轴的交点A、B的坐标;
(1)、求出图象与x轴的交点A、B的坐标;
(2)、在二次函数的图象上是否存在点P,使S△PAB= S△MAB?若存在,求出点P的坐标;若不存在,请说明理由.22. 已知:二次函数 中的 和 满足下表:…
-1
0
1
2
3
…
…
3
0
-1
0
m
…
(1)、观察上表可求得 的值为;(2)、试求出这个二次函数的解析式;(3)、若点A(n+2,y1),B(n , y2)在该抛物线上,且y1>y2 , 请直接写出n的取值范围.23. 我们知道,解一元二次方程,可以把它转化为两个一元一次方程来解,其实用“转化”的数学思想我们还可以解一些新的方程例如一元三次方程x3+x2﹣2x=0,可以通过因式分解把它转化为x(x2+x﹣2)=0,通过解方程x=0和x2+x﹣2=0,可得方程x3+x2﹣2x=0的解.(1)、方程x3+x2﹣2x=0的解是x1=0,x2= , x3= .(2)、用“转化”的思想求方程 =x的解.(3)、试直接写出 的解 .