江苏省连云港市灌云县西片2021-2022学年八年级上学期数学第一次月考试卷
试卷更新日期：2021-10-19 类型：月考试卷
一、单选题
-
1. 下列各组两个图形属于全等图形的是（ ）A、
B、
C、
D、
2. 下面4个汉字中，可以看作是轴对称图形的是（ ）A、
B、
C、
D、
3. 如图， ，其中 ， ，则 （ ）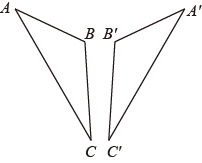
A、60° B、100° C、120° D、135°4. 如图，已知∠ABC＝∠DCB，要使△ABC≌△DCB，只需添加一个条件，这个条件不能是（ ）
A、∠A＝∠D B、∠ACB＝∠DBC C、AC＝BD D、AB＝DC5. 如图，阴影部分是由3个小正方形组成的一个图形，若在图中剩余的方格中涂黑一个正方形，使整个阴影部分成为轴对称图形，涂法有（ ）
A、2种 B、3种 C、4种 D、5种6. 在测量一个小口圆形容器的壁厚时，小明用“X型转动钳”按如图方法进行测量，其中OA＝OD，OB＝OC，测得AB＝5厘米，EF＝6厘米，圆形容器的壁厚是（ ）
A、5厘米 B、6厘米 C、2厘米 D、 厘米7. 如图，将一个三角形纸片ABC沿过点B的直线折叠，使点C落在AB边上的点E处，折痕为BD，则下列结论一定正确的是（ ）
A、AD＝BD B、BE＝AC C、ED＋EB＝DB D、AE＋CB＝AB8. 如图，在△ABC与△AEF中，AB＝AE，BC＝EF，∠ABC＝∠AEF，∠EAB＝40°，AB交EF于点D，连接EB.下列结论：①∠FAC＝40°；②AF＝AC；③∠EBC＝110°；④AD＝AC；⑤∠EFB＝40°，正确的个数为（ ）个.
A、1 B、2 C、3 D、4二、填空题
-
9. 如图是5×5的正方形网格，△ABC的顶点都在小正方形的顶点上，像△ABC这样的三角形叫格点三角形.画与△ABC有一条公共边且全等的格点三角形，这样的格点三角形最多可以画出个.
10. 如图，△ABC在平面直角坐标系中第二象限内，顶点A的坐标是（﹣2，3），先把△ABC向右平移4个单位得到△A1B1C1 ， 再作△A1B1C1关于x轴对称图形△A2B2C2 ， 则顶点A2的坐标是
11. 如图，已知△ABC≌△ADE，且点B与点D对应，点C与点E对应，点D在BC上，∠BAE=114°，∠BAD=40°，则∠E的度数是°.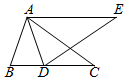
12. 如图，在Rt△ABC中，∠BAC＝90°，AB＝AC，分别过点B，C作过点A的直线的垂线BD，CE，若BD＝4cm，CE＝3cm，则DE＝cm.
13. 如图，小敏做了一个角平分仪 ，其中 ， ，将仪器上的点A与 的顶点R重合，调整 和 ，使它们分别落在角的两边上，过点A，C画一条射线 ， 就是 的平分线，小敏根据角平分仪的画图原理得到以下结论：① ，② ，③
④ ，则正确的结论有.（填序号）
14. 为迎接全国第十四届运动会，我校举行“缓堵保畅，安全出行，小手拉大手活动”每天值班老师和部分学生在校门两边站岗执勤（线段 所在区域）。如图， ， 与 相交于O， 于点D， ，已知 米，请根据上述信息求出执勤区域 的长度是.
15. 如图，AB=12，CA⊥AB于A，DB⊥AB于B，且AC=4m，P点从B向A运动，每分钟走1m，Q点从B向D运动，每分钟走2m，P、Q两点同时出发，运动分钟后△CAP与△PQB全等．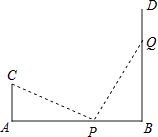
16. 如图1所示的图形是一个轴对称图形，且每个角都是直角，长度如图所示.小明按如图2所示的方法玩拼图游戏，两两相扣，相互间不留空隙，那么小明用10个这样的图形拼出来的图形的总长度是（结果用含a、b的代数式表示）.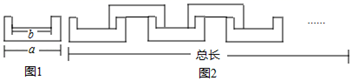
三、解答题
-
17. 如图，在2×2的正方形网格中，每个小正方形的边长均为1.请分别在下列图中画一个位置不同、顶点都在格点上的三角形，使其与 成轴对称图形.
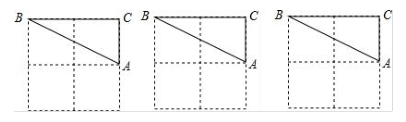18. 如图，在平面直角坐标系中，已知△ABC的三个顶点的坐标分别为A（﹣3，5），B（﹣2，1），C（﹣1，3）.
（ 1 ）画出△ABC关于x轴的对称图形△A1B1C1.
（ 2 ）画出△A1B1C1沿x轴向右平移4个单位长度后得到的△A2B2C2.
（ 3 ）如果AC上有一点M（a，b）经过上述两次变换，那么对应A2C2上的点M2的坐标是▲.
（ 4 ）△ABC的面积为 ▲.
19. 如图所示， ， ， 三点在同一直线上，且 ．
(1)、求证： ；(2)、当 满足什么条件时， ？20. 如图，四边形 与四边形 关于直线 对称.
(1)、线段 的对称线段是 ， ， ， .(2)、 与 平行吗？为什么？(3)、若 与 平行则能说明轴对称图形中对称点的连线一定互相平行吗？21. 如图，点A，F，C，D在一条直线上，AB∥DE，AB=DE，AF=DC．求证：△ABC≌△DEF．
22. 如图1，在边长为1的7×7正方形网格中，老师请同学们过点C画线段AB的垂线.如图2，小何在多媒体展台上展示了他画出的图形.请你利用所学知识判断并说明直线CD是否为线段AB的垂线.（点A，B，C，D，E，F都是小正方形的顶点）
23. 为了解学生对所学知识的应用能力，某校老师在七年级数学兴趣小组活动中，设置了这样的问题：因为池塘两端A，B的距离无法直接测量，请同学们设计方案测量A，B的距离.甲、乙两位同学分别设计出了如下两种方案：甲：如图1，先在平地上取一个可以直接到达点A，B的点O，连接AO并延长到点C，连接BO并延长到点D，使 ， ，连接DC，测出DC的长即可.
乙：如图2，先确定直线AB，过点B作直线BE，在直线BE上找可以直接到达点A的一点D，连接DA，作 ，交直线AB于点C，最后测量BC的长即可.
(1)、甲、乙两同学的方案哪个可行？(2)、请说明方案可行的理由.24. 如图a，网格中的每一个正方形的边长为1，△ABC为格点三角形，直线MN为格点直线（点A、B、C、M、N在小正方形的顶点上）.
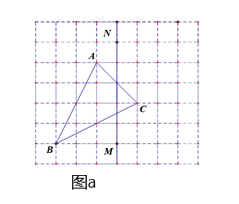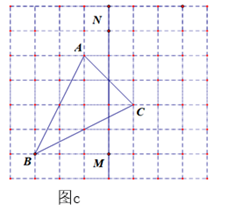
(1)、仅用直尺在图a中作出△ABC关于直线MN的对称图形△A′B′C′.(2)、如图b，仅用直尺将网格中的格点三角形ABC的面积三等分，并将其中的一份用铅笔涂成阴影.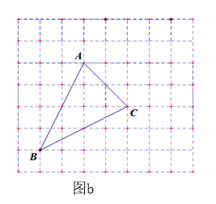
(3)、如图c，仅用直尺作三角形ABC的边AC上的高，简单说明你的理由.
