河南省平顶山市三六联校2021-2022学年八年级上学期数学第一次月考试卷

试卷更新日期：2021-10-19 类型：月考试卷

进入出卷网下载

一、单选题

1. 下列各数： $\sqrt[3]{- 3}$ ， $- \frac{π}{3}$ ， $\frac{22}{7}$ ， $\sqrt{49}$ ，0.3030030003，无理数有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
2. 满足下列条件的△ABC ，不是直角三角形的是（）

A、a：b： $c = 3$ ：4：5 B、 $∠ A$ ： $∠ B$ ： $∠ C = 9$ ：12：15 C、 $∠ C = ∠ A - ∠ B$ D、 $b^{2} - a^{2} = c^{2}$

查看试题解析
3. 下列说法不正确的是（）

A、 $\pm 0.3$ 是0.09的平方根，即 $\pm \sqrt{0.09} = \pm 0.3$ B、 $\sqrt{64}$ 的平方根是 $\pm 8$ C、正数的两个平方根的积为负数 D、存在立方根和平方根相等的数

查看试题解析
4. 下列各式计算正确的是（）

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、 $4 \sqrt{3} - 3 \sqrt{3} = 1$ C、 $2 \sqrt{3} \times 2 \sqrt{3} = 4 \sqrt{3}$ D、 $\sqrt{27} \div \sqrt{3} = 3$

查看试题解析
5. 下列二次根式中，化简后能与 $\sqrt{2}$ 合并的是（）

A、 $\sqrt{\frac{1}{2}}$ B、 $\sqrt{22}$ C、 $\sqrt{20}$ D、 $\sqrt{0.2}$

查看试题解析
6. 若△ABC的三边a，b，c，满足 ${(a - b)}^{2} + | a^{2} + b^{2} - c^{2} | = 0$ ，则△ABC是（）

A、等腰三角形 B、直角三角形 C、等腰直角三角形 D、等腰三角形或直角三角形

查看试题解析
7. 如图，矩形ABCD中， $A B = 3$ ， $A D = 1$ ，点A、B在数轴上，点A表示数－1，若以点A为圆心，对角线AC的长为半径作弧交数轴的正半轴于点M，则点M表示的数为（）

A、 $\sqrt{10}$ B、 $\sqrt{10} - 1$ C、 $\sqrt{5}$ D、2.5

查看试题解析
8. 若一个正数的两个平方根为 $a + 1$ 和 $2 a - 7$ ，则这个正数是（）

A、2 B、3 C、8 D、9

查看试题解析
9. 在 $△ A B C$ 中， $A B = 13$ ， $A C = 15$ ，高 $A D = 12$ ，则BC的长为（）

A、14 B、4 C、14或4 D、5

查看试题解析
10. 如图是一个长、宽、高分别为4cm，3cm，5cm的长方体，一只蚂蚁从顶点A出发，沿长方体的表面爬行至点B，爬行的最短路程是（）cm

A、 $5 \sqrt{2}$ B、 $\sqrt{74}$ C、 $4 \sqrt{5}$ D、12

查看试题解析

二、填空题

11. 比较大小： $\frac{\sqrt{5} - 1}{2}$ 0.5．

查看试题解析
12. 计算： $\sqrt{8} + {(- 1)}^{2020} - | - \sqrt{2} | =$ .

查看试题解析
13. 已知x，y都是实数，且y＝ $\sqrt{x - 3}$ ＋ $\sqrt{3 - x}$ ＋4，则y^x＝.

查看试题解析
14. 如图，矩形纸片ABCD中， $A B = 18 cm$ .把矩形纸片沿直线AC折叠，点B落在点E处，AE交DC于点F，若 $A F = 13 cm$ ，则AD的长为cm.

查看试题解析
15. 如图，在 $△ A B C$ 中， $A B = A C = 13$ ， $B C = 10$ ，点D为BC的中点，DE⊥AB，垂足为点E，则DE等于.

查看试题解析

三、解答题

16. 已知2a-1的平方根是±3，3a+b-9的立方根是2，c是 $\sqrt{57}$ 的整数部分.求a+2b+c的算术平方根.

查看试题解析
17. 计算下列各题

(1)、 $\sqrt{8} + \sqrt{32} - \sqrt{2}$

(2)、 $\sqrt{{(- 3)}^{2}} + \sqrt[3]{- 8} + | 1 - \sqrt{2} |$

(3)、 ${(\sqrt{3} - 1)}^{2} - (\sqrt{3} - \sqrt{2}) (\sqrt{3} + \sqrt{2})$

(4)、 $\frac{\sqrt{8} + \sqrt{18}}{\sqrt{2}} + (\sqrt{24} - \sqrt{\frac{1}{6}}) \div \sqrt{3}$

查看试题解析
18. 实数a、b、c在数轴上的对应点位置如图所示，化简： $\sqrt{{(- c)}^{2}} + | a - b | + \sqrt[3]{{(a + b)}^{3}} - | b - c |$

查看试题解析
19. 如图，网格中的 $△ A B C$ ，若小方格边长为1，请你根据所学的知识，

(1)、判断 $△ A B C$ 是什么形状？并说明理由；

(2)、求 $△ A B C$ 的面积.

查看试题解析
20. 在甲村至乙村的公路旁有一块山地正在开发，现有一 $C$ 处需要爆破．已知点 $C$ 与公路上的停靠站 $A$ 的距离为 $600$ 米，与公路上另一停靠站 $B$ 的距离为 $800$ 米，且 $C A ⊥ C B$ ，如图，为了安全起见，爆破点 $C$ 周围半径 $400$ 米范围内不得进入，问在进行爆破时，公路 $A B$ 段是否有危险，是否需要暂时封锁？请通过计算进行说明．

查看试题解析
21. 如图，四边形ABCD中，AB＝AD，∠BAD＝90°，若AB＝2 $\sqrt{2}$ ，CD＝4 $\sqrt{3}$ ，BC＝8，求四边形ABCD的面积．

查看试题解析
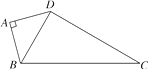22. 阅读材料：
黑白双雄、纵横江湖；双剑合璧、天下无敌.这是武侠小说中的常见描述，其意是指两个人合在一起，取长补短，威力无比.

在二次根式中也有这种相辅相成的“对子”.如： $(2 + \sqrt{3}) (2 - \sqrt{3}) = 1$ ， $(\sqrt{5} + \sqrt{2}) (\sqrt{5} - \sqrt{2}) = 3$ ，它们的积不含根号，我们说这两个二次根式互为有理化因式，其中一个是另一个的有理化因式，于是，二次根式除法可以这样理解：如： $\frac{1}{\sqrt{3}} = \frac{1 \times \sqrt{3}}{\sqrt{3} \times \sqrt{3}} = \frac{\sqrt{3}}{3}$ ， $\frac{2 + \sqrt{3}}{2 - \sqrt{3}} = \frac{(2 + \sqrt{3}) (2 + \sqrt{3})}{(2 + \sqrt{3}) (2 - \sqrt{3})} = 7 + 4 \sqrt{3}$ .像这样，通过分子、分母同乘以一个式子把分母中的根号化去或把根号中的分母化去，叫做分母有理化.

解决问题：

(1)、 $4 - \sqrt{7}$ 的有理化因式可以是， $\frac{3}{2 \sqrt{3}}$ 分母有理化得.

(2)、计算：
①已知 $x = \frac{\sqrt{3} + 1}{\sqrt{3} - 1}$ ， $y = \frac{\sqrt{3} - 1}{\sqrt{3} + 1}$ ，求 $x^{2} + y^{2}$ 的值；

② $\frac{1}{1 + \sqrt{2}} + \frac{1}{\sqrt{2} + \sqrt{3}} + \frac{1}{\sqrt{3} + \sqrt{4}} + \cdot \cdot \cdot + \frac{1}{\sqrt{1999} + \sqrt{2000}}$ .

查看试题解析
23. 如图1， $R t △ A B C$ 中， $A C ⊥ C B$ ， $A C = 15$ ， $A B = 25$ ，点D为斜边上动点.

(1)、如图2，过点D作 $D E ⊥ A B$ 交CB于点E，连接AE，当AE平分 $∠ C A B$ 时，求CE；

(2)、如图3，在点D的运动过程中，连接CD，若 $△ A C D$ 为等腰三角形，直接写出AD的值.

查看试题解析