浙江省宁波市镇海区2021-2022学年九年级上学期数学第一次月考试卷

试卷更新日期：2021-10-19 类型：月考试卷

进入出卷网下载

一、单选题

1. 抛物线y＝﹣（x+2）²﹣5的顶点坐标是（　　）

A、（2，﹣5） B、（﹣2，﹣5） C、（2，5） D、（﹣2，5）

查看试题解析
2. 若 $3 x - 4 y = 0$ ，则 $\frac{x + y}{y}$ 的值是（）

A、 $\frac{3}{7}$ B、 $\frac{7}{3}$ C、 $\frac{7}{4}$ D、 $\frac{4}{7}$

查看试题解析
3. 一枚质地均匀的骰子六个面分别标有数字1，2，3，4，5，6，投掷一次朝上一面的数字是2的倍数的概率为（）

A、 $\frac{1}{6}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{2}{3}$

查看试题解析
4. 下列说法正确的是（）

A、垂直于弦的直线必须过圆心 B、平分弦的直径垂直于弦 C、平分弧的直径平分弧所对的弦 D、三点确定一个圆

查看试题解析
5. 给出下列函数：① $y = - 3 x + 2$ ；② $y = \frac{4}{x}$ ；③ $y = 5 x^{2}$ ；④ $y = 3 x$ ，其中符合条件“当 $x > 1$ 时，函数值y随自变量x增大而增大的是（）

A、①③ B、②③ C、②④ D、③④

查看试题解析
6. 二次函数 $y = 2 x^{2} - 4 x + c$ 的最小值是0，那么c的值等于（）

A、4 B、2 C、-4 D、8

查看试题解析
7. 已知抛物线y=- $\frac{1}{6}$ x²+ $\frac{3}{2}$ x+6与x轴交于点A，点B，与y轴交于点C．若D为AB的中点，则CD的长为（）

A、 $\frac{15}{4}$ B、 $\frac{9}{2}$ C、 $\frac{13}{2}$ D、 $\frac{15}{2}$

查看试题解析
8. 如图，将△ABC放在每个小正方形边长为1的网格中，点A，B，C均落在格点上，用一个圆面去覆盖△ABC，能够完全覆盖这个三角形的最小圆面半径是（）

A、 $\sqrt{5}$ B、 $\sqrt{6}$ C、2 D、 $\frac{5}{2}$

查看试题解析
9. 如图，四边形ABCD中， $D C ∥ A B$ ， $B C = 2$ ， $A B = A C = A D = 3$ ，则BD的长为（）

A、 $\sqrt{13}$ B、5 C、 $3 \sqrt{2}$ D、 $4 \sqrt{2}$

查看试题解析
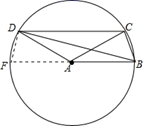10. 如图，二次函数 $y = a x^{2} + b x + c （ a \neq 0 ）$ 的图象与x轴交于点A（-2，0），与y轴的交点在（0，-2）和（0，-1）之间（不包括这两点），对称轴为直线 $x = 1$ .有下列结论：① $a b c > 0$ ；② $4 a + 2 b + c > 0$ ；③ $\frac{1}{8} < a < \frac{1}{4}$ ；④ $b < c$ .其中正确的（）

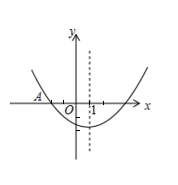A、①② B、①③ C、①④ D、③④

查看试题解析

二、填空题

11. 小强与小红两人下军棋，小强获胜的概率为46%，小红获胜的概率是30%，那么两人下一盘棋小红不输的概率是．

查看试题解析
12. 抛物线y＝(m²－2)x²－4mx＋n的对称轴是x＝2，且它的最高点在直线y＝ $\frac{1}{2}$ x＋2上，则m=,n＝.

查看试题解析
13. 如图所示，AB是⊙O的直径，弦 $C D ⊥ A B$ 于H， $∠ A = 30^{°} ， C D = 2 \sqrt{3}$ ，则⊙O的半径是.

查看试题解析
14. 如图，AB是半圆O的直径，E是弧BC的中点，OE交弦BC于点D.已知BC=8cm，DE=2cm，则AD的长为cm.

查看试题解析
15. 如图，正方形 $A B C D$ 和 $R t Δ A E F$ ， $A B = 5 ， A E = A F = 4$ ，连接 $B F ， D E$ .若 $Δ A E F$ 绕点A旋转，当 $∠ A B F$ 最大时， $S_{Δ A D E} =$ .

查看试题解析
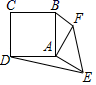16. 在直角坐标系中，抛物线y=ax²－4ax＋2(a>0)交y轴于点A，点B是点A关于对称轴的对称点，点C是抛物线的顶点，若△ABC的外接圆经过原点O，则a的值为.

查看试题解析

三、解答题

17. 如图，在⊙O中，AB=CD.求证：AD=BC.

查看试题解析

18. 已知二次函数

y = - \frac{1}{2} {(x - 1)}^{2}

(1)、完成下表；

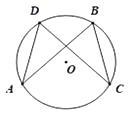$x$	$\dots$	$- 2$							$\dots$
$y$	$\dots$								$\dots$

(2)、在如图的坐标系中描点，画出该二次函数的图象.

查看试题解析

19. 已知二次函数的图象经过点 $A (- 1, 0)$ 和点 $B (3, 0)$ ，且有最小值为 $- 2$ .

(1)、求这个函数的解析式；

(2)、函数的开口方向、对称轴；

(3)、当 $y > 0$ 时， $x$ 的取值范围.

查看试题解析
20. 如图，⨀O的直径AB的长为10，弦AC的长为5，∠ACB的平分线交⨀O于点D.

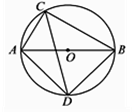(1)、求∠ADC的度数；

(2)、求弦BD的长.

查看试题解析
21. 在一个不透明的盒子里，装有三个分别写有数字1，2，3的小球，它们的形状、大小、质地等完全相同，先从盒子里随机取出一个小球，记下数字后放回盒子，摇匀后再随机取出一个小球，记下数字.请你用画树形图或列表的方法，求：

(1)、两次取出小球上的数字相同的概率；

(2)、两次取出小球上的数字之和大于3的概率.

查看试题解析
22. 如图，已知点 $A$ ， $B$ 的坐标分别为 $(0 ， 0)$ 、 $(2 ， 0)$ ，将 $Δ A B C$ 绕C点按顺时针方向旋转 $90 °$ 得到△ $A_{1} B_{1} C$ .

(1)、画出△ $A_{1} B_{1} C$ ；

(2)、A的对应点为 $A_{1}$ ，写出点 $A_{1}$ 的坐标；

(3)、求出B旋转到 $B_{1}$ 的路线长.

查看试题解析
23. 已知函数y＝（n+1）x^m+mx+1﹣n（m，n为实数）

(1)、当m，n取何值时，此函数是我们学过的哪一类函数？它一定与x轴有交点吗？请判断并说明理由；

(2)、若它是一个二次函数，假设n＞﹣1，那么：
①当x＜0时，y随x的增大而减小，请判断这个命题的真假并说明理由；

②它一定经过哪个点？请说明理由.

查看试题解析
24. 如图，点P在y轴的正半轴上，⊙P交x轴于B、C两点，以AC为直角边作等腰Rt△ACD，BD分别交y轴和⊙P于E、F两点，连接AC、FC.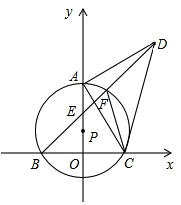

(1)、求证：∠ACF=∠ADB；

(2)、若点A到BD的距离为m，BF+CF=n，求线段CD的长；

(3)、当⊙P的大小发生变化而其他条件不变时， $\frac{D E}{A O}$ 的值是否发生变化？若不发生变化，请求出其值；若发生变化，请说明理由.

查看试题解析