浙江省杭州市上城区2021-2022学年九年级上学期数学第一次月考试卷

试卷更新日期：2021-10-19 类型：月考试卷

进入出卷网下载

一、单选题

1. 下列事件中,随机事件是（）

A、三角形中任意两边之和大于第三边 B、太阳从东方升起 C、明天会下雨 D、一个有理数的绝对值为负数

查看试题解析
2. 抛物线y＝3（x﹣1）²+1的顶点坐标是（　　）

A、（1，1） B、（﹣1，1） C、（﹣1，﹣1） D、（1，﹣1）

查看试题解析
3. 已知圆的半径为2cm，一点到圆心的距离是3cm，则这点在（）

A、圆外 B、圆上 C、圆内 D、不能确定

查看试题解析
4. 从生产的一批螺钉中抽取1000个进行质量检查，结果发现有5个是次品，那么从中任取1个是次品概率约为（）

A、 $\frac{1}{1000}$ B、 $\frac{1}{200}$ C、 $\frac{1}{2}$ D、 $\frac{1}{5}$

查看试题解析
5. 将抛物线 $y = 2 x^{2}$ 向左平移1个单位，再向下平移3个单位，则所得图象的函数解析式是（）

A、 $y = 2 {(x - 1)}^{2} + 3$ B、 $y = 2 {(x - 1)}^{2} - 3$ C、 $y = 2 {(x + 1)}^{2} + 3$ D、 $y = 2 {(x + 1)}^{2} - 3$

查看试题解析
6. 如图，正五边形 $A B C D E$ 内接于 $⊙ O$ ，则 $∠ D A E$ 的度数是（）

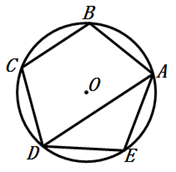A、36° B、26° C、30° D、45°

查看试题解析
7. 根据下列表格中的对应值：

x

1.98

1.99

2.00

2.01

$y = a x^{2} + b x + c$

-0.06

-0.05

-0.03

0.01

判断方程 $a x^{2} + b x + c = 0$ （ $a \neq 0$ ，a，b，c为常数）一个根x的范围是（）

A、 $1 .00 < x < 1.98$ B、 $1.98 < x < 1.99$ C、 $1.99 < x < 2.00$ D、 $2.00 < x < 2.01$

查看试题解析
8. 如图， $A B$ 是半圆O的直径， $∠ B A C = 20 °$ ，则 $∠ D$ 的度数是（）

A、70° B、100° C、110° D、120°

查看试题解析
9. 如图，已知 $⊙ O$ 的半径为5，弦 $A B = 8$ ，则 $⊙ O$ 上到弦 $A B$ 所在直线的距离为2的点有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析
10. 二次函数 $y = x^{2} + b x$ 的图象如图，对称轴为直线 $x = 1$ .若关于x的一元二次方程 $x^{2} + b x - t = 0$ （t为实数）在 $- 2 < x < 3$ 的范围内有解，则t的取值范围是（）

A、 $t \geq - 1$ B、 $- 1 \leq t < 3$ C、 $- 1 \leq t < 8$ D、 $3 < t < 8$

查看试题解析

二、填空题

11. 正八边形的一个内角的度数是度。

查看试题解析
12. 已知二次函数 $y = a x^{2} - 1 (a \neq 0)$ 有最大值为-1，则 $a =$ .（取一个适当的值即可）

查看试题解析
13. 我市倡导垃圾分类投放，将日常垃圾分成四类，分别投放四种不同颜色的垃圾桶中，在“垃圾分类”模拟活动中，某同学把两个不同类的垃圾随意放入两个不同颜色的垃圾筒中，则这个同学正确分类投放垃圾的概率是.

查看试题解析
14. 二次函数 $y = a x^{2} + b x$ 的图象如图，若一元二次方程 $a x^{2} + b x + c = 0$ 有实数根，则c的最小值为.

查看试题解析

15. 二次函数

y = a x^{2} + b x

+c（

a \neq 0

，a、b、c为常数）的部分对应值列表如下：

$x$	…	-2	-1	0	1	…
$y$	…	$- \frac{5}{2}$	-3	$- \frac{5}{2}$	-1	…

则代数式 $9 a - 3 b + 5$ 的值为.

查看试题解析

16. 如图， $O A$ 、 $O B$ 是 $⊙ O$ 的半径，且 $O A = O B = 1$ ， $A B = \sqrt{2}$ .在 $⊙ O$ 上一点C，使 $B C = \sqrt{3}$ ，则 $∠ B A C$ 的度数为.

查看试题解析

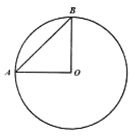
三、解答题

17.

(1)、计算： ${(- 2019)}^{0} + \sqrt{8} - 4 \times {(- \frac{1}{2})}^{2}$

(2)、先化简，再求值： $(\frac{2 x}{x - 2} - \frac{x}{x + 2}) \div \frac{x}{x^{2} - 4}$ ，其中x=-1。

查看试题解析
18. 如图，在△ABC中，∠B=∠C，F为BC的中点，D，E分别为边AB，AC上的点，且∠ADF=∠AEF。

(1)、求证：△BDF≌△CEF。

(2)、当∠A=100°，BD=BF时，求∠DFE的度数。

查看试题解析
19. 《中学生体质健康标准》规定学生体质健康等级标准为：90分及以上为优秀；80分～89分为良好；60分～79分为及格；59分及以下为不及格. 某校从九年级学生中随机抽取了 $10 %$ 的学生进行了体质测试，得分情况如下图.

(1)、在抽取的学生中不及格人数所占的百分比是，它的圆心角度数为度.

(2)、小明按以下方法计算出抽取的学生平均得分是： $(94 + 84 + 72 + 50) \div 4 = 75$ . 根据所学的统计知识判断小明的计算是否正确，若不正确，请计算正确结果.

查看试题解析
20. 各顶点都在方格纸格点（横竖格子线的交错点）上的多边形称为格点多边形.线段AB在6×6的正方形方格纸中（如图所示），点A，B均为格点，按下列要求画格点多边形.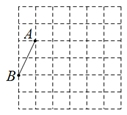

(1)、请在图甲中画一个五边形ABCDE，且是轴对称图形.

(2)、请在图乙中画一个六边形ABCDEF，且是中心对称图形.

查看试题解析
21. 如图，抛物线y=-x²+bx+c的顶点为C(3，4)，交x轴于点A，B(点B在点A的右侧)，点P在第一象限，且在抛物线AC部分上，PD⊥PC交x轴于点D。

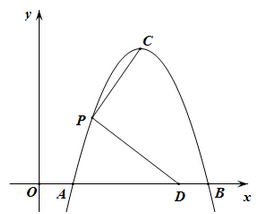(1)、求该抛物线的表达式。

(2)、若PD=3PC，求OD的长。

查看试题解析
22. 如图，△ABC内接于⊙O，AB=AC，CF垂直直径BD于点E，交边AB于点F.

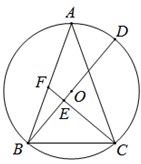(1)、求证：∠BFC=∠ABC.

(2)、若⊙O的半径为5，CF=6，求AF长.

查看试题解析
23. 某茶叶销售商计划将m罐茶叶按甲、乙两种礼品盒包装出售，其中甲种礼品盒每盒装4罐，每盒售价240元；乙种礼品盒每盒装6罐，每盒售价300元，恰好全部装完.已知每罐茶叶的成本价为30元，设甲种礼品盒的数量为x盒，乙种礼品盒的数量为y盒.

(1)、当m=120时.
①求y关于x的函数关系式.

②若120罐茶叶全部售出后的总利润不低于3000元，则甲种礼品盒的数量至少要多少盒？

(2)、若m罐茶叶全部售出后平均每罐的利润恰好为24元，且甲、乙两种礼品盒的数量和不超过69盒，求m的最大值.

查看试题解析
24. 如图，直角坐标系中，直线 y=kx+b 分别交x，y轴于点A(-8，0)，B(0，6)，C（m，0）是射线AO上一动点，⊙P过B，O，C三点，交直线AB于点D（B，D不重合）.

(1)、求直线AB的函数表达式.

(2)、若点D在第一象限，且tan∠ODC= $\frac{5}{3}$ ，求点D的坐标.

(3)、当△ODC为等腰三角形时，求出所有符合条件的m的值.

(4)、点P，Q关于OD成轴对称，当点Q恰好落在直线AB上时，直接写出此时BQ的长.

查看试题解析

x	1.98	1.99	2.00	2.01
$y = a x^{2} + b x + c$	-0.06	-0.05	-0.03	0.01