甘肃省兰州十一中教育集团2021-2022学年九年级上学期数学第一次月考试卷
试卷更新日期:2021-10-19 类型:月考试卷
一、单选题
-
1. 在下列方程中,属于一元二次方程的是( )A、 B、 C、 D、2. 将三角尺与直尺按如图所示摆放,下列关于 与 之间的等量关系正确的是( )
 A、 B、 C、 D、3. 计算 的结果是( )A、 B、 C、 D、4. 在数轴上表示不等式组 的解集,正确的是( )A、
A、 B、 C、 D、3. 计算 的结果是( )A、 B、 C、 D、4. 在数轴上表示不等式组 的解集,正确的是( )A、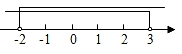 B、
B、 C、
C、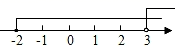 D、
D、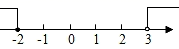 5. 多项式 因式分解为( )A、 B、 C、 D、6. 菱形具有而平行四边形不一定具有的性质是( )A、对角线互相平分 B、对角线相等 C、对角线互相垂直 D、对边平行且相等7. 如图: ,若将线段 平移至 ,则 的值为( )
5. 多项式 因式分解为( )A、 B、 C、 D、6. 菱形具有而平行四边形不一定具有的性质是( )A、对角线互相平分 B、对角线相等 C、对角线互相垂直 D、对边平行且相等7. 如图: ,若将线段 平移至 ,则 的值为( ) A、 B、 C、 D、8. 如图,在矩形纸片ABCD中,AB=8,BC=6,点P在AB上,将△DAP沿DP折叠,使点A落在对角线BD上的点A′处,则AP的长为( )
A、 B、 C、 D、8. 如图,在矩形纸片ABCD中,AB=8,BC=6,点P在AB上,将△DAP沿DP折叠,使点A落在对角线BD上的点A′处,则AP的长为( ) A、2 B、3 C、4 D、59. 今年,某中学响应习总书记“足球进校园”的号召,开设了“足球大课间”活动,现需要购进100个某品牌的足球供学生使用,经调查,该品牌足球2019年单价为200元,2021年单价为162元,2019年到2021年该品牌足球单价平均每年降低的百分率是( )A、10% B、19% C、20% D、30%
A、2 B、3 C、4 D、59. 今年,某中学响应习总书记“足球进校园”的号召,开设了“足球大课间”活动,现需要购进100个某品牌的足球供学生使用,经调查,该品牌足球2019年单价为200元,2021年单价为162元,2019年到2021年该品牌足球单价平均每年降低的百分率是( )A、10% B、19% C、20% D、30%二、填空题
-
10. 若分式 的值为零,则a的值为 .11. 如图,直线AB CD,GH平分∠CGF,GI平分∠DGF,且HG=15cm,GI=20cm,HI=25cm,则直线AB与直线CD之间的距离是cm.
 12. 如图,线段AB=10,分别以点A,点B为圆心,以6为半径作弧,两弧交于点C,点D,连接CD.则CD的长为.
12. 如图,线段AB=10,分别以点A,点B为圆心,以6为半径作弧,两弧交于点C,点D,连接CD.则CD的长为. 13. 已知,如图,正方形 中,线段 绕点A逆时针旋转60°得到线段 ,连接 ,点F为 中点, 的延长线交 的延长线于点G,连接 .下列结论:① ;② ;③ ;④ ,其中正确的结论有.(填写所有正确结论的序号)
13. 已知,如图,正方形 中,线段 绕点A逆时针旋转60°得到线段 ,连接 ,点F为 中点, 的延长线交 的延长线于点G,连接 .下列结论:① ;② ;③ ;④ ,其中正确的结论有.(填写所有正确结论的序号)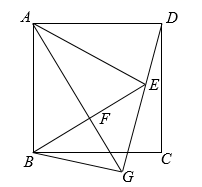
三、解答题
-
14. 计算: .15. 解一元二次方程:2x2﹣2x﹣1=0.16. 先化简,再求值:(1﹣ )÷ ,其中x=﹣1.17. 为满足市场需求,新生活超市在端午节前夕购进价格为3元/个的粽子,根据市场预测,该品牌粽子每个售价4元时,每天能出售500个,并且售价每上涨0.1元,其销售量将减少10个.为了维护消费者利益,物价部门规定,该品牌棕子的售价不能超过进价的200%.(1)、该品牌粽子每个售价为5元,则每天出售 个.(2)、该品牌粽子定价为多少元时,该超市每天的销售利润为800元.18. 为了调查学生对垃圾分类及投放知识的了解情况,从甲、乙两校各随机抽取40名学生进行了相关知识测试,获得了他们的成绩(百分制),并对数据(成绩)进行了整理、描述和分析下面给出了部分信息.
a.甲、乙两校40名学生成绩的频数分布统计表如下:
成绩x
学校
50≤x<60
60≤x<70
70≤x<80
80≤x<90
90≤x≤100
甲
4
11
13
10
2
乙
6
3
15
14
2
(说明:成绩80分及以上为优秀,70~79分为良好,60~69分为合格,60分以下为不合格)
b.甲校成绩在70≤x<80这一组的是:70;70 ;70; 71; 72 ;73 ;73; 73 ;74 ;75 ;76; 77; 78
c.甲、乙两校成绩的平均分、中位数、众数如下:
学校
平均分
中位数
众数
甲
74.2
n
85
乙
73.5
76
84
根据以上信息,回答下列问题:
(1)、写出表中n的值为;(2)、在此次测试中,某学生的成绩是74分.在他所属的学校排前20名,由表中数据可知该学生是校的学生(填“甲”或“乙”),理由是.(3)、现从样本90~100的4名学生中任意抽取2名学生参加“环保知识竞赛”,请用画树状图或列表的方法求出刚好抽到甲、乙两校学生各一名的概率.19. 如图,在边长为1的小正方形网格中,点A,B,C均落在格点上.
( 1 )求△ABC的面积?
( 2 )画出△ABC关于直线l的轴对称图形△A1B1C1.
( 3 )在直线l上有一点P使PC+PB最小,请画出点P.
20. 已知关于x的一元二次方程x2﹣(k+3)x+2k+2=0.(1)、求证:不论k为何值,方程总有两个实数根;(2)、若方程有一个根小于1,求k的取值范围.21. 小张骑自行车匀速从甲地到乙地,在途中休息了一段时间后,仍按原速行驶,他距乙地的距离y(km)与时间x(h)的关系如图中折线所示,小李开车匀速从乙地到甲地,比小张晚出发一段时间,他距乙地的距离y(km)与时间x(h)的关系如图中线段AB所示. (1)、小李到达甲地后,再经过小时小张也到达乙地;小张骑自行车的速度是千米/小时.(2)、小张出发几小时与小李相距15千米?(3)、若小李想在小张休息期间与他相遇,则他出发的时间x应在什么范围?(直接写出答案)22. 如图,在△ABC中,∠B=90°,AB=5cm,BC=7cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动.若P,Q两点同时出发,当点Q运动到点C时,P,Q两点同时停止运动.求:
(1)、小李到达甲地后,再经过小时小张也到达乙地;小张骑自行车的速度是千米/小时.(2)、小张出发几小时与小李相距15千米?(3)、若小李想在小张休息期间与他相遇,则他出发的时间x应在什么范围?(直接写出答案)22. 如图,在△ABC中,∠B=90°,AB=5cm,BC=7cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动.若P,Q两点同时出发,当点Q运动到点C时,P,Q两点同时停止运动.求: (1)、几秒后,PQ的长度等于2 cm?(2)、△PBQ的面积能否等于7cm2?说明理由.23. 如图1,在△ABC中,AB=AC,AD是△ABC的一条角平分线,AN为△ABC的外角∠BAM的平分线,BE⊥AN,垂足为E.已知AD=4,BD=3.
(1)、几秒后,PQ的长度等于2 cm?(2)、△PBQ的面积能否等于7cm2?说明理由.23. 如图1,在△ABC中,AB=AC,AD是△ABC的一条角平分线,AN为△ABC的外角∠BAM的平分线,BE⊥AN,垂足为E.已知AD=4,BD=3. (1)、求证:四边形ADBE是矩形;(2)、如图2,延长AD至点F,使AF=AB,连接BF,G为BF的中点,连接EG,DG.求EG的长.(3)、如图3,在(2)问的条件下,P为BE边上的一个动点,连接PG并延长交AD延长线于点Q,连接CQ,H为CQ的中点,求点P从E点运动到B点时,点H所经过的路径长.
(1)、求证:四边形ADBE是矩形;(2)、如图2,延长AD至点F,使AF=AB,连接BF,G为BF的中点,连接EG,DG.求EG的长.(3)、如图3,在(2)问的条件下,P为BE边上的一个动点,连接PG并延长交AD延长线于点Q,连接CQ,H为CQ的中点,求点P从E点运动到B点时,点H所经过的路径长.