福建省宁德市2021-2022学年九年级上学期数学第一次质量检测试卷
试卷更新日期:2021-10-19 类型:月考试卷
一、单选题
-
1. 如果 ,那么 的值为( )A、 B、 C、 D、
-
2. 如图,四边形ABCD的对角线AC , BD相交于点O , 且AC⊥BD , 则下列条件能判定四边形ABCD为菱形的是( )
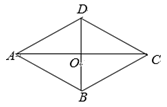 A、AB=CD B、OA=OC , OB=OD C、AC=BD D、 ,AD=BC
A、AB=CD B、OA=OC , OB=OD C、AC=BD D、 ,AD=BC -
3. 为增强学生环保意识,某中学举办了环保知识竞赛,某班共有3名学生(2名男生,1名女生)获奖.老师若从获奖的3名学生中任选两名作为班级的“环保小卫士”,则恰好是一名男生、一名女生的概率为( )A、 B、 C、 D、
-
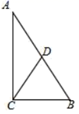
4. 如图,在△ABC中,AC=3,BC=6,D为BC边上的一点,且∠BAC=∠ADC . 若△ADC的面积为a , 则△ABC的面积为( )
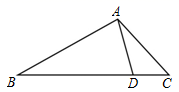 A、6a B、4a C、 D、
A、6a B、4a C、 D、 -
5. 若m是方程 的一个根,设 , ,则p与q的大小关系为( )A、p<q B、p=q C、p>q D、与c的取值有关
-
6. 如图,在反映特殊四边形之间关系的知识结构图中,①②③④表示需要添加的条件,则下列描述错误的是( )
 A、①表示有一个角是直角 B、②表示有一组邻边相等 C、③表示四个角都相等 D、④表示对角线相等
A、①表示有一个角是直角 B、②表示有一组邻边相等 C、③表示四个角都相等 D、④表示对角线相等 -
7. 若关于x的一元二次方程(k﹣1)x2+2x﹣2=0有不相等实数根,则k的取值范围是( )A、k> B、k≥ C、k> 且k≠1 D、k≥ 且k≠1
-
8. 三角形两边长分别是8和6,第三边长是一元二次方程x2﹣16x+60=0一个实数根,则该三角形的面积是( )A、24 B、48 C、24或8 D、8
-
9. 如图,△ABC中,AB=6,AC=4,以BC为对角线作正方形BDCF , 连接AD , 则AD长不可能是( )
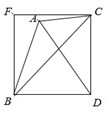 A、2 B、4 C、6 D、8
A、2 B、4 C、6 D、8 -
10. 七巧板是中国传统数学文化的重要载体,利用七巧板可以拼出许多有趣的图案.现用图1所示的一副七巧板拼成如图2所示的六边形,若图1中七巧板的总面积为16,则图2中六边形的周长为( )
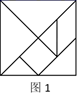
 A、 B、 C、 D、
A、 B、 C、 D、
二、填空题
-
11. 如图,在 中, ,D是边 的中点,若 ,则 .
-
12. 方程 的根是 .
-
13. 在一个不透明的布袋中,蓝色,黑色,白色的玻璃球共有20个,除颜色外其他完全相同.将布袋中的球摇匀,从中随机摸出一个球,记下它的颜色再放回去,通过多次摸球试验后发现,摸到黑色、白色球的频率分别稳定在10%和35%,则口袋中蓝色球的个数很可能是 .
-
14. 小白有两张卡片,分别标有数字1,2;小黄有三张卡片,分别标有数字3,4,5.两人各自随机地取出一张卡片,取出的两张卡片上数字之积为奇数的概率是.
-
15. 《算学宝鉴》全称《新集通证古今算学宝鉴》,王文素著,完成于明嘉靖三年,全书12本42卷,近50万字,代表了我国明代数学的最高水平.《算学宝鉴》中记载的用导数解高次方程的方法堪与牛顿媲美,且早于牛顿140年.《算学宝鉴》中记载了我国南宋数学家杨辉提出的一个问题:“直田积八百六十四步,之云阔不及长十二步,问长阔共几何?”
译文:一个矩形田地的面积等于864平方步,且它的宽比长少12步,问长与宽的和是多少步?如果设矩形田地的长为x步,可列方程为 .
-
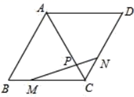
16. 如图,在边长为10的菱形 中, 为对角线, ,M、N分别是边 , 上的点, ,连接 交 于P点,当 最短时, 长度为.
三、解答题
-
17. 解方程:
-
18. 已知关于x 的一元二次方程x2 -5x + m = 0.(1)、若方程有实数根,求实数m 的取值范围;(2)、若方程两实数根为x1 , x2 , 且满足3 x1-2x2 =5,求实数m 的值.
-
19. 如图,在 中, ,D是 的中点,E是 的中点,过点A作 交 的延长线于点F.
 (1)、求证:四边形 是菱形;(2)、若 , ,求菱形 的面积.
(1)、求证:四边形 是菱形;(2)、若 , ,求菱形 的面积. -
20. 第七次全国人口普查于2020年11月1日开展,某学校积极响应所在社区的号召,选派部分教师参与普查,其中数学组有4位教师志愿报名,分别记为甲、乙、丙、丁.(1)、若该校从数学组教师志愿者中抽调1位教师作为普查员,求教师甲被选中的概率.(2)、若该校从数学组教师志愿者中抽调2位教师作为普查员,请用列表或画树状图的方法,求出教师甲和乙被选中的概率.
-
21. 如图,矩形ABCD中,AB=6,点E在AB上,且BE=2,四边形EFGH为菱形,且点F , H分别在边BC , AD上.
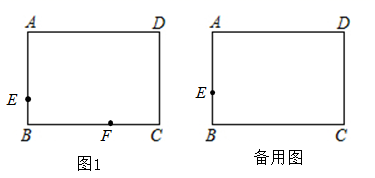 (1)、当点F的位置如图1所示,请用尺规作出菱形EFGH . (保留作图痕迹,不写作法)(2)、若菱形EFGH为正方形,求四边形EFGH的面积.
(1)、当点F的位置如图1所示,请用尺规作出菱形EFGH . (保留作图痕迹,不写作法)(2)、若菱形EFGH为正方形,求四边形EFGH的面积. -
22. “中秋节”前,某超市第一次以80元/盒的进价购进一款月饼礼盒500盒,以120元/盒的售价全部销售完.销售人员根据市场调研发现,该款月饼礼盒每盒的售价在120元基础上每降价5元,销量就会相应增加100盒,该超市计划第二次购进该款月饼礼盒,但不超过650盒.(1)、在进价不变的情况下,第二次实际售价在第一次基础上降了a元时,则该超市这款月饼每盒利润为元,预计销售量为 盒.(2)、在(1)的条件下,若第二次的销售总利润比第一次增加5%,求a的值.
-
23. 四边形的一条对角线把这个四边形分成两个三角形,如果这两个三角形相似(不全等),我们就把这条对角线称为这个四边形的“理想对角线”.
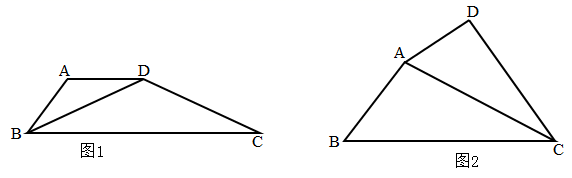 (1)、如图1,在四边形ABCD中,∠ABC=70°,AB=AD , AD∥BC , 当∠ADC=145°时.
(1)、如图1,在四边形ABCD中,∠ABC=70°,AB=AD , AD∥BC , 当∠ADC=145°时.求证:对角线BD是四边形ABCD的“理想对角线”.
(2)、如图2,四边形ABCD中,AC平分∠BCD , 当∠BCD与∠BAD满足什么关系时,对角线AC是四边形ABCD的“理想对角线”,请说明理由. -
24. 已知关于x的一元二次方程: .(1)、求证:该方程始终有两个实数根.(2)、已知该方程有一个固定解,求出这个解.(3)、若 ,设方程两根为 , ,且 ,当整数n至少可取到2个整数,求a的取值范围.
-
25. 如图,点E,F在正方形ABCD的对角线AC上, .
 (1)、当BE=BF时,求证:AE=CF;(2)、若AB=4,求 的值;(3)、延长BF交CD于点G,连接EG.判断线段BE与EG的数量关系,并说明理由.
(1)、当BE=BF时,求证:AE=CF;(2)、若AB=4,求 的值;(3)、延长BF交CD于点G,连接EG.判断线段BE与EG的数量关系,并说明理由.
