四川省成都市2020-2021学年高一上学期数学期末考试试卷
试卷更新日期:2021-10-18 类型:期末考试
一、单选题
-
1. 设全集 ,集合 , ,则 ( )A、 B、 C、 D、2. 下列函数中,与函数 相等的是( )A、 B、 C、 D、3. 已知角 的顶点与直角坐标系的原点重合,始边与 轴的非负半轴重合,且 .若角 的终边上有一点 ,则 的值为( )A、-4 B、4 C、-3 D、34. 设函数 则 的值为( )A、2 B、3 C、 D、5. 已知扇形的圆心角为30°,面积为 ,则扇形的半径为( )A、 B、3 C、 D、66. 函数 的零点所在区间是( )A、 B、 C、 D、7. 已知函数 ,则函数 的递减区间是( )A、 B、 C、 D、8. 函数 的图象大致为( )A、
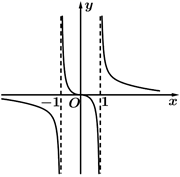 B、
B、 C、
C、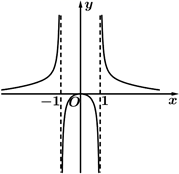 D、
D、 9. 已知函数 ,先将函数 图象上各点的横坐标伸长到原来的2倍(纵坐标不变),再将所得到的图象向右平移 个单位长度,最后得到函数 的图象,则 的值为( )A、1 B、 C、0 D、10. 已知函数 在 上单调递减,则实数 的取值范围是( )A、 B、 C、 D、11. 若 , , ,则 , , 的大小关系为( )A、 B、 C、 D、12. 设函数 , .若 的值不小于0,则 的取值范围是( )A、 B、 C、 D、
9. 已知函数 ,先将函数 图象上各点的横坐标伸长到原来的2倍(纵坐标不变),再将所得到的图象向右平移 个单位长度,最后得到函数 的图象,则 的值为( )A、1 B、 C、0 D、10. 已知函数 在 上单调递减,则实数 的取值范围是( )A、 B、 C、 D、11. 若 , , ,则 , , 的大小关系为( )A、 B、 C、 D、12. 设函数 , .若 的值不小于0,则 的取值范围是( )A、 B、 C、 D、二、填空题
-
13. 计算 的值为 .14. 已知函数 ( 且 )的图象恒过定点 ,则 的值为 .15. 已知函数 是定义在 上的偶函数,且对区间 上的任意 , ,当 时,都有 .若实数 满 ,则 的取值范围是 .16. 已知函数 在 上单调,且将函数 的图象向右平移4π个单位长度后与原来的图象重合.当 时,使得不等式 成立的 的最大值为 .
三、解答题
-
17. 计算下列各式的值:(1)、 ;(2)、 .18. 已知 ,且 .
(Ⅰ)求 , 的值;
(Ⅱ)求 的值.
19. 已知函数 .(Ⅰ)用函数单调性的定义证明函数 在 上是增函数;
(Ⅱ)当 时,求函数 的最值.
20. 1986年4月26日,一场地震造成乌克兰境内的切尔诺贝利核电站爆炸并引起大火.这一事故导致约8吨的强辐射物严重泄露,事故所在地被严重污染.主要辐射物是锶90,它每年的衰减率为2.47%,经专家模拟估计,辐射物中锶90的剩余量低于原有的8.46%时,事故所在地才能再次成为人类居住的安全区;要完全消除这次核事故对自然环境的影响至少需要800年.设辐射物中原有的锶90有 吨.(1)、设经过 年后辐射物中锶90的剩余量为 吨,试求 的表达式,并计算经过800年后辐射物中锶90的剩余量;(2)、事故所在地至少经过多少年才能再次成为人类居住的安全区?(结果保留为整数)参考数据: , .