江西省抚州市2020-2021学年高一上学期数学期末考试试卷(B卷)
试卷更新日期:2021-10-18 类型:期末考试
一、单选题
-
1. 下列各角中,与68°角终边相同的是( )A、22° B、248° C、428° D、728°2. 已知集合 , ,则 ( )A、 B、 C、 D、3. 已知函数 则 ( )A、 B、 C、 D、4. 要得到函数 的图象,只需要将函数 的图象( )A、向右平移 个单位长度 B、向左平移 个单位长度 C、向右平移 个单位长度 D、向左平移 个单位长度5. 已知平面向量 , 的夹角为 ,且 ,则 ( )A、 B、 C、 D、6. 下列函数中,既是偶函数又在区间 上单调递减的是( )A、 B、 C、 D、7. 已知a是函数 的零点,则函数 的零点所在的区间为( )A、 B、 C、 D、8. 已知 , , ,则( )A、 B、 C、 D、9. 函数 的图象大致为( )A、
 B、
B、 C、
C、 D、
D、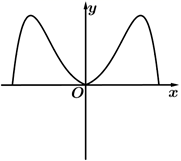 10. 已知函数 ,下列说法正确的是( )A、点 是 图象的一个对称中心 B、 的最小正周期是 C、 在区间 上的最大值为 D、 在区间 上是减函数11. 已知 , ,则 ( )A、 B、 C、 D、12. 已知 ,且 , ,则 ( )A、 B、 C、 D、
10. 已知函数 ,下列说法正确的是( )A、点 是 图象的一个对称中心 B、 的最小正周期是 C、 在区间 上的最大值为 D、 在区间 上是减函数11. 已知 , ,则 ( )A、 B、 C、 D、12. 已知 ,且 , ,则 ( )A、 B、 C、 D、二、填空题
-
13. 已知平面向量 , ,若 ,则 .14. 已知幂函数f(x)的图象经过点(3, ),则f(4)= .15. 定义在 上的奇函数 在 上是减函数,若 ,则m的取值范围为.16. 在平行四边形 中, , 分别是边 , 上的两点,且 , ,若 ,则 .
三、解答题
-
17. 已知向量 , .(1)、求 的值;(2)、若 ,求实数λ的值.18. 已知 为第二象限角,且 .(1)、求 的值;(2)、若 ,求 的值.19. 已知函数 的部分图象如图所示.
 (1)、求 的解析式;(2)、求 的单调递增区间.
(1)、求 的解析式;(2)、求 的单调递增区间.