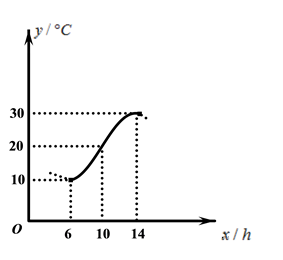湖南省湘西自治州2020-2021学年高一上学期数学期末考试试卷
试卷更新日期:2021-10-18 类型:期末考试
一、单选题
-
1. 若集合 , ,则 ( )A、 B、{0} C、{1} D、2. 设命题 ,则 为( )A、 B、 C、 D、3. “角 是第一或第三象限角”是“ ”的( )A、充分非必要条件 B、必要非充分条件 C、充要条件 D、既不充分也不必要条件4. 的图象是连续不间断的曲线,且有如下对应值
1
2
3
4
5
6
124
35
-74
14.5
-56.7
-123.6
则 在区间 上的零点至少有( )
A、2个 B、3个 C、4个 D、5个5. 若 ,则 与 在同一坐标系中的图象大致是( )A、 B、
B、 C、
C、 D、
D、 6. 为了得到函数 的图像,只需把 图象上的所有点( )A、向右平移 个单位长度 B、向左平移 个单位长度 C、向右平移 个单位长度 D、向左平移 个单位长度7. 中国的5G技术领先世界,5G技术的数学原理之一便是著名的香农公式: .它表示:在受噪声干扰的信道中,最大信息传递速度 取决于信道带宽 ,信道内信号的平均功率 ,信道内部的高斯噪声功率 的大小,其中 叫做信噪比.当信噪比比较大时,公式中真数中的1可以忽略不计.按照香农公式,若不改变带宽 ,而将信噪比 从1000提升至4000,则 大约增加了( )附:A、10% B、20% C、50% D、100%8. 下列各函数中,与函数 同一函数的是( )A、 B、 C、 D、9. 下述四个结论
6. 为了得到函数 的图像,只需把 图象上的所有点( )A、向右平移 个单位长度 B、向左平移 个单位长度 C、向右平移 个单位长度 D、向左平移 个单位长度7. 中国的5G技术领先世界,5G技术的数学原理之一便是著名的香农公式: .它表示:在受噪声干扰的信道中,最大信息传递速度 取决于信道带宽 ,信道内信号的平均功率 ,信道内部的高斯噪声功率 的大小,其中 叫做信噪比.当信噪比比较大时,公式中真数中的1可以忽略不计.按照香农公式,若不改变带宽 ,而将信噪比 从1000提升至4000,则 大约增加了( )附:A、10% B、20% C、50% D、100%8. 下列各函数中,与函数 同一函数的是( )A、 B、 C、 D、9. 下述四个结论①若 ,则 ②已知扇形的半径 ,圆心角30°,则扇形的弧长是 ③函数 是单调递增函数④化简 得到的结果是 其中所有正确结论的编号是( )
A、①② B、②③ C、②④ D、②③④10. 已知 , ,且 .下述四个结论① ;② ;③ ;④ .
其中所有正确结论的编号是( )
A、①②③ B、①②④ C、①③④ D、②③④二、填空题
-
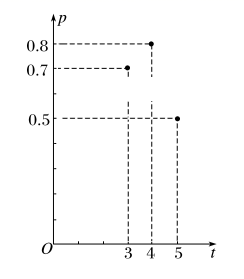
11. 已知幂函数 的图象经过点 ,则 的解析式是 .12. 函数 的定义域是 .13. 已知角 、 的顶点在原点,始边在x轴的非负半轴上,它们的终边与单位圆分别相交于 , 两点,则 .14. 加工爆米花时,爆开且不糊的粒数占加工总粒数的百分比称为“可食用率”.在特定条件下,可食用率p与加工时间t(单位:分钟)满足函数关系 (a , b , c是常数),如图记录了三次实验的数据.根据上述函数模型和实验数据,可以得到最佳加工时间为分钟.
 15. 设 是定义在R上、以1为周期的函数,若 在 上的值域为 ,则 在区间 上的值域为 .
15. 设 是定义在R上、以1为周期的函数,若 在 上的值域为 ,则 在区间 上的值域为 .三、解答题
-
16.(1)、计算: ;(2)、已知 , ,求 的值.17. 张军自主创业,在网上经营一家干果店,销售的干果中有松子、开心果、腰果、核桃价格依次为120元/千克、80元/千克、70元/千克、40元千克,为增加销量,张军对这四种干果进行促销:一次购买干果的总价达到150元及以上,顾客就少付 元.每笔订单顾客网上支付成功后,张军会得到支付款的80%.(1)、若顾客一次购买松子和腰果各1千克,需要支付180元,试求x的值.(2)、在促销活动中,为保证张军每笔订单得到的金额均不低于促销前总价的七折,试求x的最大值.